SOLUTION: Are the points A(6,4),B(8,6),C(4,8) and D(2,4) vertices of a square? Find its area

No way is that a square!  Maybe you meant A(6,2) and not A(6,4).  I'll consider
both cases in the event that's what you meant.

I will go ahead and find the area of the (non-square) polygon whose vertices
are A(6,4), B(8,6), C(4,8), and D(2,4), then I'll look at the case where
you might have meant A(6,2) and not A(6,4)

Since the polygon is convex (doesn't "sink in" anywhere). we use the
determinant formula, whose rows are the coordinates in counter-clockwise
order, with the first row repeated at the bottom:



To expand it add the sum of the products of the diagonals going down
to the right and subtract the sum of the products of the diagonals
going up to the right:

[]  

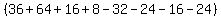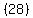If you meant for point A to be A(6,2) and not (6.4) and just mistyped,
then the figure would have been a square.

line(2,4,6,4), line(6,4,8,6), line(8,6,4,8), line(4,8,2,4) )}}} 



We can show that is a square by drawing in some (green) right triangles,
forming a little square in the middle:



Those 4 green right triangles have one leg 2 units long,
and the other leg 4 units long. They are all congruent
and so their hypotenuses all have the same length. That
shows the quadrilateral is at least a rhombus.  Each internal
angle of ABCD is the sum of two complementary angles (acute
angles of a right triangle).  I'll let you fill in the details
as to why the internal angles of rhombus ABCD are 90° each.

Each of the four green right triangles have an area of 
.  So four of them makes 16 square units.

The little square in the middle is 2×2 so its area is 4, and so the area
of the square is 16+4 or 20 square units.

We could also have used the determinant method which we used to get the 
first area above which wasn't a square

[]

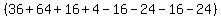Edwin