Question 1208799: ABCD is a quadrilateral. If diagonals AC and BD bisect each other, then prove that ABCD is a parallelogram.
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!
E = intersection of diagonals AC and BD
By construction we'll have EA = EC and EB = ED be the case.
Let's say we placed point E at the origin (0,0).
Let's place point A at (p,q) where p and q are any real numbers. I'll select p = 2 and q = 3 as shown in the diagram below.
To go from E to A we go p units right and q units up.
To go from E to C, we go in reverse: go p units left and q units down. This places C at (-p,-q)
By construction, AE = EC to show that diagonal AC is bisected.
You can use the distance formula, or Pythagorean theorem, to show that  and  , to arrive at 
Now let's say point B is located at (r,s) where r and s are any real numbers. I'll pick r = 3 and s = 1.
Follow similar logic as the previous paragraph to determine point D is located at (-r,-s).
A similar construction leads to BE = ED to show that diagonal BD is bisected.
-------------------------------------------------------
Key takeaway:
A = (p,q)
B = (r,s)
C = (-p,-q)
D = (-r,-s)
E = (0,0)
In the diagram above we have p=2,q=3,r=3,s=1.
However, you can select any four real numbers you want for p,q,r,s.
-------------------------------------------------------
Compute the slope of side AB
m = (y2-y1)/(x2-x1)
m = (s-q)/(r-p)
Compute the slope of side CD
m = (y2-y1)/(x2-x1)
m = (-s-(-q))/(-r-(-p))
m = (-s+q)/(-r+p)
m = (-1(s-q))/(-1(r-p))
m = (s-q)/(r-p)
Both slope results are the same expression. To avoid dividing by zero,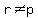 
Since slopeAB = slopeCD, we conclude that AB is parallel to CD.
Similar steps are followed to prove that BC is parallel to AD.
This concludes the proof that ABCD is a parallelogram.
Answer by ikleyn(52784)  (Show Source):
|
|
|
