SOLUTION: In the diagram below, BPCR is a rhombus, P is (0,6), C is (6,t) and B is (2,0). The Line PR and BC bisect at Q, PR = 2BC and PR =8sqrt 2 find 1, the value of t? 2, the co o

From just this information.

BPCR is a rhombus, P is (0,6), C is (6,t) and B is (2,0).

we know that C(6,t) is somewhere on the vertical line whose
equation is x=6 (the green line.




we know that since it is a rhombus, PC must equal
PC, so we can draw side BP, take a compass and swing an arc like
this red one with radius BP, and find only two possibilities
for point C, th points where the arc cuts the green line:



So the rhombus is one of these two:



Since we are told that PR = 2BC, we know it must be the second one,
not the first.



Since all the sides of a rhombus are equal in
length, we use the distance formula to find BP:





We use the distance formula again to set the
BP = PC =  √40





Square both sides:





take square roots of both sides:





So t=4 or 8.  Obviously the answer we 
want is  C(6,4),

So t=4

We can get the coordinates of R just by
counting units.  We know that B is 6
units down and 2 units right from P.
So R must be 6 units down and 2 units
right from C.  That would give us R(8,-2).

We could also get the coordinates of R 
this way.  We know that C is 6
units right and 2 units down from P.
So R must be 6 units right and 2 units
down from B.  That would also give us 
R(8,-2).

If we like can check to make sure that 

PR = 2BC and PR =8sqrt 2

by using the distance formula, but
that's obvious if this is a legitimate
problem.

To find the equation of PR, the blue line below:



To find the equation of the PR, the blue line, we use 
the slope formula to find the slope:

Slope formula:
m = 
where 

P(x1,y1) = P(0,6)
and where R(x2,y2) = R(8,-2)

m =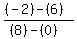 
m = 
m = 1

Then we use the point-slope formula:
y - y1 = m(x - x1)
where (x1,y1) = (0,6)

y - 6 = 1(x - 0)
y - 6 = x
    y = x + 6

Edwin