SOLUTION: An isoceles triangle whose are is 1200 square meters and height 40m is cut parallel to its non-congruent side producing a trapezoid and a triangle whose areas are equal. Find the h

Algebra ->  Parallelograms -> SOLUTION: An isoceles triangle whose are is 1200 square meters and height 40m is cut parallel to its non-congruent side producing a trapezoid and a triangle whose areas are equal. Find the h      Log On


   

Question 1012945: An isoceles triangle whose are is 1200 square meters and height 40m is cut parallel to its non-congruent side producing a trapezoid and a triangle whose areas are equal. Find the height of the new triangle and the height of the trapezoid.
Answer by josgarithmetic(39630) About Me  (Show Source):
You can put this solution on YOUR website!
The triangle before making the cut:
Altitude 40, unknown base b, area 1200.
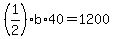
%281%2F2%29b%2A40=1200
highlight%28b=60%29

Same or congruent triangle, now draw a segment through the altitude, this segment parallel to the b=60 base. The upper region is another isosceles triangle with altitude h and base x. The lower region is trapezoid with altitude a and TWO bases are x and 60.
-
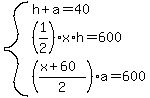
system%28h%2Ba=40%2C%281%2F2%29x%2Ah=600%2C%28%28x%2B60%29%2F2%29%2Aa=600%29
That is according to the description of the two regions being of equal areas, and the two heights being the original given triangle height (altitudes).
-
Note this is a system of three equations in three unknown variables.

system%28h%2Ba=40%2Chx=1200%2Cxa%2B60a=1200%29

Use first equation as h=40-a, and substitute into the other two equations,
system%2840-ax=1200%2Cax%2B60a=1200%29
and observing that both of these have a term, ax;
ax=1200-60a
SUBSTITUTE into ...
40-%281200-60a%29=1200
doing the steps,
..
..
highlight%28a=39%261%2F3%29---height for the trapezoid.

Still want to find h and for this, return to h%2Ba=40.
highlight%28h=2%2F3%29.--------height for the triangle.