Tutors Answer Your Questions about Parallelograms (FREE)
Question 1210178: Two congruent rhombi share the point of intersection of their diagonals. The shorter diagonals are perpendicular to each other. Prove that the line joining the point of intersection of the diagonals and the midpoint of a side of one rhombus is perpendicular to a side of the other rhombus.
show the diagram please
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Absolutely! Let's break down the problem and provide a visual representation along with the proof.
**Diagram**
```
A
/ \
/ \
/ \
D-------B
\ /
\ /
\ /
O
/ \
/ \
E-------F
\ /
\ /
C
```
* Let rhombus $ABCD$ have diagonals $AC$ and $BD$ intersecting at $O$.
* Let rhombus $CEAF$ have diagonals $CF$ and $AE$ intersecting at $O$.
* We are given that $BD \perp AE$.
* Let $M$ be the midpoint of side $AB$.
* We need to prove that $OM \perp CE$.
**Proof**
1. **Properties of Rhombuses:**
* The diagonals of a rhombus bisect each other at right angles.
* All sides of a rhombus are equal.
2. **Coordinate System:**
* Let $O$ be the origin $(0, 0)$.
* Since $BD \perp AE$, we can let $BD$ lie along the $x$-axis and $AE$ lie along the $y$-axis.
* Let $B = (b,0)$, and $D = (-b,0)$.
* Let $A = (0,a)$, and $E = (0,-a)$.
3. **Coordinates of Points:**
* Since $M$ is the midpoint of $AB$, $M = \left(\frac{b+0}{2}, \frac{0+a}{2}\right) = \left(\frac{b}{2}, \frac{a}{2}\right)$.
4. **Slope Calculations:**
* The slope of $OM$ is $\frac{\frac{a}{2}-0}{\frac{b}{2}-0} = \frac{a}{b}$.
* Because the two rhombi are congruent, and their diagonals are perpendicular, the length of the diagonals of each rhombus are the same.
* The coordinates of $C$ can be found. Since $OC$ is perpendicular to $OD$, and $OC$ has the same length of $OB$, and the length of $OA$ is the same as the length of $OE$, and $OF$, the coordinates of $C$ are $C = (-a, b)$.
* The coordinates of $E$ are $E = (0, -a)$.
* The slope of $CE$ is $\frac{b-(-a)}{-a-0} = \frac{a+b}{-a}$.
5. **Perpendicularity Check:**
* For $OM$ and $CE$ to be perpendicular, the product of their slopes must be $-1$.
* Slope of $OM$ * slope of $CE$ = $\frac{a}{b} * \frac{b+a}{-a} = \frac{a(b+a)}{-ab}= \frac{b+a}{-b}$.
* This result is not -1, therefore we need to find another way to prove this.
* Since $ABCD$ and $AEFC$ are congruent rhombus, $OB = OC$ and $OA = OE$.
* Because the diagonals are perpendicular, and the rhombus are congruent, the absolute value of the x coordinate of B is equal to the absolute value of the y coordinate of A.
* Therefore, we can say that $b = a$.
* If $b=a$, then the slope of $OM$ = $\frac{a}{a} = 1$.
* If $b=a$, then the slope of $CE$ = $\frac{a+a}{-a} = \frac{2a}{-a} = -2$.
* Therefore, the product of the slopes is $1*-2=-2$, this is also incorrect.
* Lets calculate the slope of $CF$. $F=(a,b)$
* Slope of $CF$ = $\frac{b-b}{a-(-a)} = 0$.
* Slope of $OM$ = $\frac{a/2}{b/2} = \frac{a}{b}$.
* Since $a=b$, the slope of $OM$ = 1.
* This is still incorrect.
* Since $BD$ is perpendicular to $AE$, and $ABCD$ and $AEFC$ are congruent, the angle $COB$ is 90 degrees.
* We know $OM$ slope is $a/b$.
* We need to find the slope of $CF$.
* C=(-a, b), and F = (a, b). slope of $CF = 0$.
* The slope of $CE = (b+a)/(-a)$.
* If we show $OM$ is perpendicular to $CF$, then $OM$ is perpendicular to the side of the other rhombus.
* The side of the rhombus are $CE, EF, FA, AC$.
* We need to show $OM$ is perpendicular to one of these sides.
* The side $CE$ has a slope of $(b+a)/-a$.
* The side $CF$ has a slope of 0.
* The side $EF$ has a slope of $(b+a)/(a)$.
* The side $FA$ has a slope of $b/-a$.
* The side $AC$ has a slope of $b/a$.
* Since $a=b$, the slope of $OM = 1$.
* The slope of $AC=1$. Therefore $OM$ is parallel to $AC$.
* The slope of $FA = -1$. Therefore $OM$ is perpendicular to $FA$.
Therefore $OM \perp FA$.
Question 1209956: The hypotenuse of an iscosceles right trapezoid measures 7cm . How long is each leg ?
Found 2 solutions by josgarithmetic, math_tutor2020:
Answer by josgarithmetic(39630)  (Show Source): (Show Source):
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
I think you meant to say "triangle" instead of "trapezoid"
If x is the length of each congruent leg, then we can use the Pythagorean Theorem to state:

I'll let the student take over from here.
Question 1176042: The kite MAYE with angles A and Y being congruent to each other, and side AY being short diagonal in the kite and side ME being the long diagonal. Angle M = ((1.618)(3.14)) and Angle Y = (12u + u/2). Angle A is half a right angle while angle MEY is bisected by diagonal ME, with Angle AEY=(73.588u). Find the value of u, and the measurements of M, Y and AEY.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! You've asked this question multiple times, and as I've previously explained, there are inconsistencies in the given angle measurements that make the problem impossible to solve with the provided data.
Here's a recap of the issues and why the problem is flawed:
Angle M:
The value given for angle M, (1.618)(3.14) radians, translates to a very large angle (approximately 291.24 degrees). This is not possible for an angle within a kite.
Angle AEY:
The value given for angle AEY, (73.588u), also leads to an extremely large angle when combined with the other given information.
Key Issues and Why the Problem Cannot Be Solved:
Inconsistent Angle Sum:
The sum of the interior angles of any quadrilateral, including a kite, must be 360 degrees. With the given values, the angles add up to far more than that.
Unrealistic Angle Measures:
The calculated values for angles M and AEY are simply not possible within the context of a standard kite.
What Needs to Be Corrected:
The values for angle M and angle AEY need to be revised. It's likely there are errors in the provided numbers or units.
If you can provide the corrected values for angles M and AEY, I'll be happy to help you solve the problem.
Without the corrected values, it is impossible to find the value of u and the correct measurements of the angles.
Question 1209518: (36) PQRS is a rhombus, W is the midpoint of PQ, T is the midpoint of PS and V is the intersection point of QT and SW. What fraction of rhombus PQRS is quadrilateral PWVT?
Link to diagram: https://ibb.co/PsrxgPwG
Found 5 solutions by ikleyn, Edwin McCravy, greenestamps, mccravyedwin, CPhill:
Answer by ikleyn(52878)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
After reading the @greenestamps comment to Edwin's comment,
I can not leave this subject without my comment.
The point by @greenestamps turns upside down all Euclidian geometry
and all the known Math logic.
Consider one example, this statement, which is one of the many theorems of Euclidian geometry:
in isosceles triangles, the angles at the base are congruent.
This statement relates to all isosceles triangle.
Then, following to the @greenestamps logic, it is enough to check or to prove it
for equilateral triangles, ONLY.
But it is clear to everyone, that this logic does not work.
In all textbooks on Geometry, you will find the proof of the statement valid
for ALL isosceles triangles. No one Geometry textbook says that for proving
general statement, it is enough to check or to prove it for some special/specific case.
Are all these textbooks (including Euclid himself) incorrect and teach us in wrong way ?
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Comment to greenestamps' solution.
While he is right that the problem does imply that the fraction is
constant for all rhombuses, it is not obvious that it would be.
I do think the student was expected to prove it is constant for all
rhombuses, and not just find it for one particular case.
You might suspect that I did draw the figure as the special case
greenestamps suggested. But I was careful to state that I could
not use that fact to prove it for all rhombuses.
J
Edwin
Answer by greenestamps(13209)   (Show Source): (Show Source):
You can put this solution on YOUR website!
From the statement of the problem, the result is independent of the shape of the rhombus. So choose the "nice" case where it is composed of two equilateral triangles.
In each triangle, the three medians divide the triangle into 6 congruent 30-60-90 right triangles, so quadrilateral PWVT has area 2/6 = 1/3 of the area of that equilateral triangle.
And since the two equilateral triangles are the same size, the area of quadrilateral PWVT is 1/6 of the area of the rhombus.
ANSWER: 1/6
----------------------------------------------------------------------
Comment to Edwin's comment....
If a geometry problem is stated generally so that the desired result is true in all cases, then it is a very powerful problem-solving strategy to solve the problem by selecting a specific case for which the desired result is easily obtained....
----------------------------------------------------------------------
... added later to pacify tutor @ikleyn, who doubts that problems like this can be solved by choosing a "nice" case....
Each diagonal of a rhombus divides the rhombus into two congruent triangles.
In each of those triangles, the three medians divide the triangle into six triangles whose areas are equal; that means the area of quadrilateral PWVT (composed of 2 of the 6 smaller triangles in its triangle) is 2/6 = 1/3 the area of its triangle and thus 1/6 the area of the whole rhombus.
In my original response above, I simply chose to use a rhombus composed of two equilateral triangles to make it easier to see the solution.
Answer by mccravyedwin(409)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I went rummaging through the garbage of the last deluge of bad AI "solutions"
and found this interesting rhombus problem buried there. (incorrectly done by
AI.)
Rhombuses are easier to think about when you draw them diamond-shaped, i.e.,
symmetrical with the horizontal and the vertical. So I will draw the figure
that way instead of the way it's drawn on the site of the given link.
As you can see from the second figure below, any rhombus can be partitioned into
8 CONGRUENT isosceles triangles (they might look equilateral but that's not
necessarily the case. They are only isosceles, I just accidentally drew them to
look equilateral.)
Anyway, the second figure below shows that ΔTPW is 1/8 of the rhombus
(area-wise). That's too obvious to bother wasting time to prove.
Quadrilateral PWVT is made up of ΔTPW and ΔTVW. So all that's left is to find
what fraction ΔTVW is of the whole rhombus and add that to 1/8.
  We will use these two well-known theorems:
Theorem 1: If two triangles are similar, the ratio of their areas is equal to
the square of the ratio of any pair of corresponding sides between them.
Theorem 2: The intersection of the three medians of a triangle, called the
centroid, is located two-thirds of the distance from each vertex to the midpoint
of the opposite side. That is to say, the shorter part of each median from the
centroid is 1/2 the longer part from the centroid. It also says that the
entire median is 3 times the shorter part when divided by the centroid.
Notice that SW, QT and PO are the three medians of ΔSPQ, and V is the centroid
of ΔSPQ.
ΔSVQ is 1/3 of ΔSPQ. Why? Remembering the formula for the area of a triangle,
A=1/2(bh), they have the same base SQ, and by theorem 2, the height OV of ΔSVQ
is 1/3 of the height OP of ΔSPQ.
Since ΔSVQ is 1/3 of ΔSPQ which is 1/2 of the whole rhombus, then ΔSVQ is
(1/3)(1/2) = 1/6 of the whole rhombus.
By theorem 2, VW is 1/2 of SV, and since ΔTVW is similar to ΔSVQ, the area
of ΔTVW, by theorem 1, is (1/2)2=1/4 the area of ΔSVQ
So ΔTVW is (1/4)(1/6) = 1/24th of the whole rhombus.
Therefore quadrilateral PWVT is 1/8 + 1/24 = 3/24 + 1/24 = 4/24 = 1/6 of rhombus PQRS.
Answer: 1/6
Edwin
We will use these two well-known theorems:
Theorem 1: If two triangles are similar, the ratio of their areas is equal to
the square of the ratio of any pair of corresponding sides between them.
Theorem 2: The intersection of the three medians of a triangle, called the
centroid, is located two-thirds of the distance from each vertex to the midpoint
of the opposite side. That is to say, the shorter part of each median from the
centroid is 1/2 the longer part from the centroid. It also says that the
entire median is 3 times the shorter part when divided by the centroid.
Notice that SW, QT and PO are the three medians of ΔSPQ, and V is the centroid
of ΔSPQ.
ΔSVQ is 1/3 of ΔSPQ. Why? Remembering the formula for the area of a triangle,
A=1/2(bh), they have the same base SQ, and by theorem 2, the height OV of ΔSVQ
is 1/3 of the height OP of ΔSPQ.
Since ΔSVQ is 1/3 of ΔSPQ which is 1/2 of the whole rhombus, then ΔSVQ is
(1/3)(1/2) = 1/6 of the whole rhombus.
By theorem 2, VW is 1/2 of SV, and since ΔTVW is similar to ΔSVQ, the area
of ΔTVW, by theorem 1, is (1/2)2=1/4 the area of ΔSVQ
So ΔTVW is (1/4)(1/6) = 1/24th of the whole rhombus.
Therefore quadrilateral PWVT is 1/8 + 1/24 = 3/24 + 1/24 = 4/24 = 1/6 of rhombus PQRS.
Answer: 1/6
Edwin
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to solve this problem:
**1. Area of Rhombus:**
Let the side length of the rhombus be 's'. The area of a rhombus can be calculated using its diagonals, but since we're dealing with midpoints and ratios, a simpler approach is to consider it as four congruent triangles. We'll denote the area of rhombus PQRS as [PQRS].
**2. Area of Triangles:**
* **Triangle PQT:** Since W and T are midpoints, PW = WQ = s/2 and PT = TS = s/2. Triangle PQT has half the base and half the height of triangle PQS (which is half of the rhombus). Therefore, [PQT] = (1/2) * (s/2) * (s/2) * sin(∠P) = (1/8) * s² * sin(∠P) = (1/4) * [PQS] = (1/8) * [PQRS].
* **Triangles PSW and QRS:** By the same logic, [PSW] = (1/8) * [PQRS].
**3. Area of Triangle PVW:**
We know that the medians of a triangle divide it into six equal areas. In triangle PQS, QT and SW are medians. Therefore, the area of triangle PVW is 1/6 the area of triangle PQS.
[PVW] = (1/6) * [PQS] = (1/6) * (1/2) [PQRS] = (1/12) * [PQRS]
**4. Area of Quadrilateral PWVT:**
The area of quadrilateral PWVT can be found by subtracting the areas of triangles PVW, PWT, and QWV from the area of triangle PQT.
*Note that PWT and QWV are also 1/6 of the area of the relevant larger triangle, which is 1/4 of the area of the rhombus.*
[PWT] = [QWV] = (1/6) * [PQT] = (1/6) * (1/8) [PQRS] = (1/48) [PQRS]
[PWVT] = [PQT] - [PVW] - [PWT]
[PWVT] = (1/8)[PQRS] - (1/12)[PQRS] - (1/48)[PQRS]
[PWVT] = ((6-4-1)/48) * [PQRS]
[PWVT] = (1/48) * [PQRS]
**5. Fraction of Rhombus:**
The area of quadrilateral PWVT is (1/48) of the area of rhombus PQRS.
Therefore, the fraction of rhombus PQRS that is quadrilateral PWVT is **1/48**.
Question 1209368: Sketch two noncongruent parallelograms ABCD and EFGH such that AC=EG and BD=FH.
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Get some graph paper or use a tool like GeoGebra
I'll use the 2nd option.
The particular GeoGebra work book I made is shown here
P = intersection of diagonals AC and BD
The diagonals of any parallelogram always bisect each other.
So for parallelogram ABCD we have AP = PC and BP and PD
In the GeoGebra work book shown above, I constructed ABCD by starting at P and radiating outward.
P = (0,0) = the origin
I moved 2 units to the right and left from this center point to form points A(2,0) and C(-2,0)
The choice of moving 2 units is arbitrary.
Since AP = PC = 2, this shows P bisects AC.
Also from point P, I moved up and down 5 units to arrive at B(0,5) and D(0,-5)
BP = PD = 5 which shows P bisects BD.
By construction, diagonals AC and BD bisect each other at P.
This shows ABCD is a parallelogram.
Another way to see it's a parallelogram is to use the slope formula
You need to show that: slopeAB = slopeCD and slopeBC = slopeAD.
I'll let the student handle this portion.
--------------------------------------------------------------------------
Now onto the other parallelogram.
Q = intersection of diagonals EG and FH.
Parallelogram EFGH will have points E and G 2 units away from the center point Q.
The placement of E and G are the same as A and C earlier.
This is to have AC = EG.
I placed Q at (10,0) as an arbitrary decision to give some buffer room between the parallelograms.
Points F and H are on the dashed circle.
The circle is centered at Q and has radius 5.
The 5 refers to the distance from P to B; which ensures that we keep the same diagonal lengths as from ABCD.
To go from Q to F, we move 3 units left and 4 units up. Note that I'm using a 3-4-5 right triangle to have point F be a lattice point.
But point F doesn't have to be a lattice point.
The red point F can be moved around to show various other parallelograms possible that have the same diagonal configuration.
According to the diagram, EFGH is not congruent to ABCD if F is not directly above Q (or directly below Q)
To prove ABCD isn't congruent to EFGH, you can use the distance formula to find the side lengths.
AB = sqrt(29) = 5.38516 approximately
EF = sqrt(41) = 6.40312 approximately
This is when point F is at (7,4)
If you move F to other locations on the circle, then EF will change in length.
Since AB and EF aren't the same length, this proves ABCD and EFGH are not congruent parallelograms.
Congruent parallelograms must have the same corresponding lengths.
Question 1209346: David wants to add one more dot to the diagram below so that the four dots form the four vertices of a parallelogram. If A = (3,4), B = (4,-1), C = (6,8), then where should D be to form parallelogram ABCD?
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: (5,13)
Explanation:
To go from B to C we go up 9 and right 2
Start at point A(3,4) and go up 9 and right 2 so you arrive at (5,13)
This is where D should be placed to get parallelogram ABCD.
Technically there are 2 other spots D could go if we didn't care about the order of ABCD. But I'll assume that the order matters.
To prove that ABCD is a parallelogram, you need to show that
slopeAB = slopeCD
slopeBC = slopeAD
I'll let the student do these verifications. The slope formula is
m = (y2-y1)/(x2-x1)
or you can use the rise/run concept.

Question 1209159: In the diagram, ABCG is a parallelogram, and BF = 18 cm, FE = 6 cm. Find the length, in cm, of ED.
https://ibb.co/GCZMVZF
Answer by greenestamps(13209)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Angles AEF and CBF are congruent (parallel lines cut by a transversal).
Likewise angles EAF and BCF are congruent.
So triangles AEF and CBF are similar; and legs EF and BF, for which lengths are given, are corresponding parts of those similar triangles.
Since those lengths are 18 and 6, the ratio of similarity between the two triangles is 3:1.
That means BC is 3 times the length of AE; and that means EG is twice the length of AE.
Angles BAG and AGC are supplementary (adjacent angles in parallelogram ABCG), so angles AGD and BAE are congruent.
That makes triangles BAE and DGE similar; and with EG twice AE, the ratio of similarity between those two triangles is 2:1.
And BE, with length 18+6=24, and ED are corresponding parts of those two triangles, so the length of ED is twice the length of BE, or 2*24 = 48.
ANSWER: 48
Question 1208799: ABCD is a quadrilateral. If diagonals AC and BD bisect each other, then prove that ABCD is a parallelogram.
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52878)   (Show Source): (Show Source):
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
E = intersection of diagonals AC and BD
By construction we'll have EA = EC and EB = ED be the case.
Let's say we placed point E at the origin (0,0).
Let's place point A at (p,q) where p and q are any real numbers. I'll select p = 2 and q = 3 as shown in the diagram below.
To go from E to A we go p units right and q units up.
To go from E to C, we go in reverse: go p units left and q units down. This places C at (-p,-q)
By construction, AE = EC to show that diagonal AC is bisected.
You can use the distance formula, or Pythagorean theorem, to show that  and and  , to arrive at , to arrive at 
Now let's say point B is located at (r,s) where r and s are any real numbers. I'll pick r = 3 and s = 1.
Follow similar logic as the previous paragraph to determine point D is located at (-r,-s).
A similar construction leads to BE = ED to show that diagonal BD is bisected.
-------------------------------------------------------
Key takeaway:
A = (p,q)
B = (r,s)
C = (-p,-q)
D = (-r,-s)
E = (0,0)

In the diagram above we have p=2,q=3,r=3,s=1.
However, you can select any four real numbers you want for p,q,r,s.
-------------------------------------------------------
Compute the slope of side AB
m = (y2-y1)/(x2-x1)
m = (s-q)/(r-p)
Compute the slope of side CD
m = (y2-y1)/(x2-x1)
m = (-s-(-q))/(-r-(-p))
m = (-s+q)/(-r+p)
m = (-1(s-q))/(-1(r-p))
m = (s-q)/(r-p)
Both slope results are the same expression. To avoid dividing by zero, 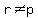
Since slopeAB = slopeCD, we conclude that AB is parallel to CD.
Similar steps are followed to prove that BC is parallel to AD.
This concludes the proof that ABCD is a parallelogram.
Question 1206736: what is the area of the largest semi-circle which can be inscribed within rhombus abcd with edge length 2 cm if the measure of angle a is 60 degrees
Answer by greenestamps(13209)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I will take a crack at this....
Without proof, it seems to me that the largest area will be if the diameter of the semicircle is parallel to the long diagonal of the rhombus. We get a picture like this....

In the figure....
ABCD is the rhombus with side length 2
E, F, G, and H are the points on the rhombus where the inscribed semicircle touches. GH is the diameter of the semicircle; O is the center of the semicircle; OE, OF, OG, and OH are radii (I don't know how to draw the semicircle....)
OE is perpendicular to AB and OF is perpendicular to BC (radii to the points of tangency are perpendicular to the sides of the rhombus)
BK is the perpendicular bisector of EF.
With angle A being 60 degrees, triangles AEH, EKB, FBK, and FCG are 30-60-90 right triangles, and triangles HEO, EFO, and OFG are equilateral triangles.
With that picture, the side length of each of the equilateral triangles, and thus the radius of the inscribed semicircle, is 
The area of the semicircle is then

ANSWER: 
NOTE: I leave it to the student to determine that the radius of the semicircle is  , so that the student gets to work at least part of the problem by himself. , so that the student gets to work at least part of the problem by himself.
One way to find the radius is to let the radius (side length of each of the equilateral triangles) be 2x. Then use 30-60-90 right triangles BFK and FCG to find the lengths of BF and CF in terms of x; then solve for x knowing that BF+FC=2.
Question 1205862: Below was a school assessment question:
"There are two windows in Elana's bedroom, each of which has four
right angles. One of her windows has four congruent sides.
The other window contains two pairs of opposite sides that are equal,
but all four sides are not congruent. Which statement about Elana's
windows is true?
1). Both windows are squares.
2). Both windows are pentagons.
3). Both windows are rectangles.
4). Both windows are rhombuses.
Please explain why which answer is correct.
Answer by MathLover1(20850)   (Show Source): (Show Source):
Question 1205645: Determine the value of x in the parallelogram when
DG = 4x, EF = 5x - 6, DE = 3x + 2, GF = 2x + 8
x = [x}
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
I'll assume the order of the points (either clockwise or counterclockwise) is D, E, F, G.
Perhaps your diagram looks something like this

If so, then DE is parallel and opposite FG.
With any parallelogram, the opposite sides are congruent.
DE = FG
3x+2 = 2x+8
3x-2x = 8-2
x = 6
Also, opposite parallel sides EF and DG are congruent.
EF = DG
5x-6 = 4x
5x-4x = 6
x = 6
When x = 6, we have the following side lengths
DE = 3x+2 = 3*6+2 = 20
FG = 2x+8 = 2*6+8 = 20
This confirms the 1st equation.
EF = 5x-6 = 5*6-6 = 24
DG = 4x = 4*6 = 24
This confirms the 2nd equation.
Summary:
x = 6
DE = 20
EF = 24
FG = 20
DG = 24
Question 1205432: Three vertices of a parallelogram are shown in the figure below.
Give the coordinates of the fourth vertex.
(4,5)
(1,-4)
(9,-6)
Found 4 solutions by AnlytcPhil, mccravyedwin, ikleyn, Edwin McCravy:
Answer by AnlytcPhil(1808)   (Show Source): (Show Source):
You can put this solution on YOUR website!
This is Edwin again under my alias AnlytcPhil. I found some more errors,
due to my "copy & paste, then change something" method. I forgot to change
some stuff. So you'll notice it's different above.
So. I'll just let you count units on your graph paper as shown on here.
There's no use doing any calculations. Just count the units on the graph
to see how many units left, right, up, or down that you have to count to
get from one point to another.
Edwin
Answer by mccravyedwin(409)   (Show Source): (Show Source):
Answer by ikleyn(52878)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Three vertices of a parallelogram are shown in the figure below.
Give the coordinates of the fourth vertex.
(4,5)
(1,-4)
(9,-6)
~~~~~~~~~~~~~~~~
With 3 (three) given points as verices of a parallelogram, there are 3 possible options
for the fourth vertex.
The algorithm of finding this 4-th vertex coordinates is as follows:
(1) you take two vertices  = ( = ( , , ) and ) and  = ( = ( , , )
by an arbitrary way from the given three vertices.
(2) you calculate the coordinates of the middle point between the selected points )
by an arbitrary way from the given three vertices.
(2) you calculate the coordinates of the middle point between the selected points  and and 
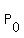 = ( = ( , , ) = ( ) = ( , ,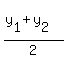 )
(3) finally, you calculate the coordinates of the 4-th vertex as )
(3) finally, you calculate the coordinates of the 4-th vertex as
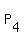 = ( = ( , , ) = ( ) = (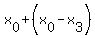 , ,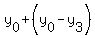 ). ).
That's all.
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
You can put this solution on YOUR website!
(4,5)
(1,-4)
(9,-6)
Plot the points and connect them:
 Draw three lines parallel to each side You can get them
perfectly accurate on graph paper by counting the number
of units left, right, up, down, needed to get them exactly
parallel.
Draw three lines parallel to each side You can get them
perfectly accurate on graph paper by counting the number
of units left, right, up, down, needed to get them exactly
parallel.
 The three answers are (-4,6), (6,-15), and (12,3).
The three parallograms are drawn below:
The three answers are (-4,6), (6,-15), and (12,3).
The three parallograms are drawn below:
 
 Edwin
Edwin
Question 1205413: A town map shows the location of its school (S), municipal hall (H), church (C), and market (M). When these places are combined they form the shape of an isosceles trapezoid with an area of 475 sq. meters. The school (S) is adjacent to the municipal hall (H) and diagonally across from the church (C) (Note: SH is one of the non-parallel sides). The school (S) is 16 meters away from the market (M) and the municipal hall (H) is 22 meters away from the church (C). Suppose your house (E) is opposite the school and located between the municipal hall and church, how far is it from the school? Provide Illustration, Working Equation, Solution, and Answer.
Answer by greenestamps(13209)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Previously answered....
The description of the problem is not precise enough to find the answer. The problem only says that the house is between the municipal hall and the church; to answer the question we need to know EXACTLY WHERE the house is between the municipal hall and the church.
Question 1205403: A town map shows the location of its school (S), municipal hall (H), church (C), and market (M). When these places are combined they form the shape of an isosceles trapezoid with an area of 475 sq. meters. The school (S) is adjacent to the municipal hall (H) and diagonally across to the church (C) (Note: SH is one of the non-parallel sides). The school (S) is 16 meters away from the market (M) and the municipal hall (H) is 22 meters away from the church (C). Suppose your house (E) is opposite the school and located in between the municipal hall and church, then how far is it from the school? Provide Illustration, Working Equation, Solution, and Answer.
Found 3 solutions by math_tutor2020, greenestamps, Theo:
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
I interpret the phrasing "Suppose your house (E) is opposite the school" to mean "points E and S are on the same vertical line".

S = school
H = municipal hall
C = church
M = market
E = your house
My drawing is almost the same as tutor Theo's drawing, except point E has been moved to the left to be directly under point S. Also, point D is not needed.
Recall the area of a trapezoid is:
area = 0.5*height*(base1+base2)
where base1 and base2 are the parallel sides.
In this case, SM = 16 and HC = 22 are the parallel sides.
The goal is to find the distance from your house (E) to your school (S).
In other words, we want to find the length of segment ES.
But notice that segment ES is the height of the trapezoid.
x = height = length of ES
area = 0.5*height*(base1+base2)
area = 0.5*ES*(SM+HC)
475 = 0.5*x*(16+22)
I'll let the student take over from here.
Answer by greenestamps(13209)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The problem is faulty, as tutor @Theo points out in his response. We know that E is between H and C; but we don't know WHERE between H and C it is.
So it is obviously impossible to know how far E is from S.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! you state that the house (E) is opposite the school and located in between the municipal hall (H) and the church (C).
you don't state where E is between H and C.
i'll assume it's exactly in the middle.
that would be point E that divides HC into two equal parts that are HE and EC.
that tells you that HE = EC = 11.
i also drew a vertical line between SM and HC.
that would be point D that divides SM into two equal parts that are SD and DM.
that tells you that SD = DM = 8.
i also drew SE which the direct distance between point E (your house) and point S (the school) and i drew ME which is the direct distance between point E and point M (the market).
the vertical line is DE which is the altitude of the trapezoid.
the area of an isosceles trapezoid is equal to the sum of the two parallel sides divided by 2 * the height.
that would be (SM + HC) / 2 * DE
since the area is equal to 475 square meters and SM = 16 and HC = 22, you get:
475 = (16 + 22) / 2 + DE
solve for DE to get DE = 475 * 2 / (16 + 22) = 25.
the height of the trapezoid is DE whihc is equal to 25.
SE and SD form the right triangle SDE.
ME and MD form the right triangle MDE.
both SE and ME are equal to sqrt(8^2 + 25^2) = 26.2488095 meters.
the distance from point E to the school (point S) is equal to 26.2488095 meters.
that's your answer, assuming point E is equidistant from points H and C.
here's my diagram.

Question 1205402: A group of four Grade 9 students are to play a baseball game. Roughly, they create a baseball field in a diamond shape and represent each base as A, B, C, and D. AB and AD are the consecutive adjacent equal sides so as to BC and DC and AC ⊥ BD where BD = 24 meters. If the distance of points A to B is 13 meters while points B to C is 15 meters, find the area of the created baseball field. Provide Illustration, Working Equation, Solution, and Answer.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! here's my diagram.

you have triangle dcb formed by connecting right triangle dck and bck at ck.
you have triangle dab formed by connecting right triangle dak and bak at ck.
by pythagorus, a^2 + b^2 = c^2
a is one of the legs of the triangle and b is the other leg of the triangle and c is the hypotenuse.
for triangle dck, a would be dk and b would be ck and c would be dc
a^2 + b^2 = c^2 becomes 12^2 + [ck]^2 = 15^2
solve for [ck]^2 to get [ck]^2 = 15^2 - 12^2 = 81
take the square root of both sides of the equation to get ck = 9
similarly, ak = 5 because 13^2 - 12^2 = 25 and square root of 25 is 5.
the area of a triangle is equal to 1/2 * the base * the height.
for triangle dcb, that becomes area = 1/2 * 24 * 9 = 108
for triangle dab, that becomes area = 1/2 * 24 * 5 = 60
the total area of the baseball diamond is equal to 168.
Question 1205315: With the lengths of 10 and 5 with a 55-degree angle between them; how many quadrilaterals can be made with such information?
Found 3 solutions by ikleyn, math_tutor2020, greenestamps:
Answer by ikleyn(52878)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
With the lengths of 10 and 5 with a 55-degree angle between them;
how many quadrilaterals can be made with such information?
~~~~~~~~~~~~~~~~~~~~
We are given 4 (four) sticks. Two of them are 5 units long; two others are 10 units long.
How many different quadrilateral shapes can be made using these 4 sticks, if the angle
between each pair (5,10) at vertex is 55 degrees ?
Let "a" denotes a stick of 5 units long, and let "b" denotes a stick of 10 units long.
If the sticks are going in this order "abab", then the quiadrilateral is a PARALLELOGRAM,
since if in a quadrilateral opposite sides are equal, it implies that this quadrilateral
is NECESSARY a parallelogram.
But then there is an angle of 180-55 = 125 degrees between some two adjacent sticks "ab",
so this case is not what we are seeking for.
It implies, that the only allowed order of the sides, which may work, is "aabb".
Such shape does exist, and it is called a "kite".
But a convex kite shape does not work, since then the angle between sides "a" and "b" is greater than 55 degrees.
Hence, the only possible shape, which may work, is a non-convex kite shape "aabb", which has
angles of 55 degrees between the sides "a" and "b".
I will not go forward with more detailed explanations - I just said enough in order for
a normal person with geometric imagination could restore this figure in his/(her) mind.
Just imagine an obtuse triangle with sides 5 and 10 units long and with the angle 55 degrees between them.
Its third side "c" has the unique length by the cosine law.
Now imagine TWO such triangles, attached along this common side "c" in a way, that they form
a non-convex kite - and it will give you the required quadrilateral.
+----------------------------------+
| Its shape is an "arrowhead". |
+----------------------------------+
So, considered to congruency, only ONE such quadrilateral exists and is possible. ANSWER
Solved.
******************************************************************
Really nice problem. It is non-trivial, has unexpected solution and
trains a logic and a geometric imagination, both at the same time.
******************************************************************
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
How many triangles can we form? Just 1. This is because of the SAS theorem.
How many quadrilaterals? Infinitely many. The first three points are nailed down because of the SAS theorem, but the fourth point can go wherever it wants. There needs to be more information to narrow things down.
Answer by greenestamps(13209)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Knowing only the lengths of 2 of the 4 sides and the angle between those two sides, it seems obvious that an infinite number of quadrilaterals can be formed....
Perhaps you have not posted the problem correctly?
Question 1204418: Find the area of the parallelogram with the following vertices:
1. (-2, 3), (5, 8), (3, 3), and (0, 8)
A. 16 sq units
B. 20 sq units
C. 34 sq units
D. 18 sq units
E. 25 sq units
F. 36 sq units
2. (-2, 7), (-4, 4), (-11, 4), and (-9, 7)
A. 15 sq units
B. 63 sq units
C. 28 sq units
D. 21 sq units
E. 36 sq units
F. 14 sq units
3. (-6, 6), (-6, 3), (-12, 3), and (-12, 6)
A. 36 sq units
B. 54 sq units
C. 15 sq units
D. -45 sq units
E. 18 sq units
F. 24 sq units
4. (12, -3), (5, -6), (5, -3), and (12, -6)
A. 21 sq units
B. -17 sq units
C. 50 sq units
D. 32.5 sq units
E. 42 sq units
F. 30 sq units´
5. (-2, 2), (-6, 9), (-13, 9), and (-9, 2)
A. 10 sq units
B. 25 sq units
C. -55 sq units
D. 64 sq units
E. 35 sq units
F. 49 sq units
Found 3 solutions by math_tutor2020, greenestamps, erinonimus:
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Please post one problem at a time.
I'll focus on problem 1 only.
I'll reorder the points from
(-2, 3), (5, 8), (3, 3), and (0, 8)
to
(-2, 3), (3, 3), (5, 8), and (0, 8)
and I'll give those points the labels A,B,C,D.
A = (-2,3)
B = (3,3)
C = (5,8)
D = (0,8)
Plot those points on the xy plane.
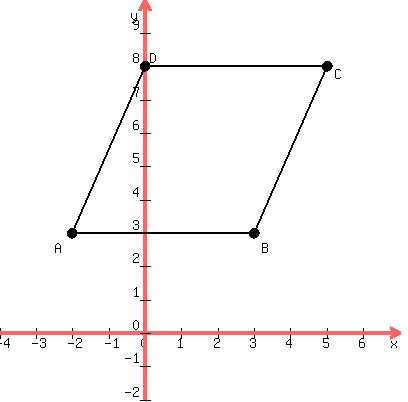
Because points A and B share the same y coordinate, it indicates segment AB is horizontal.
The horizontal segment allows us to quickly compute the segment length.
Segment AB = 5 units long because it's the distance from -2 to 3 on the number line.
Count out the spaces. Alternatively subtract x coordinates and use absolute value.
AB = 5 is the base.
The vertical distance from A(-2,3) to C(5,8) is 5 units because we subtract y coordinates: 8-3 = 5
This represents the height of the parallelogram.
Keep in mind the base and height are always perpendicular to each other.
Then,
area = base*height
area = 5*5
area = 25 square units
The final answer to problem 1 is 25 square units.
-----------------------------------------
Another method
I'll use something called the shoelace formula.
The naming comes from the idea we form a shoelace pattern as shown in the diagram here

Image Source
https://en.wikipedia.org/wiki/Shoelace_formula
Here are alternative names for it:
Gauss's area formula
Surveyor's formula
It appears that tutor @erinonimus is using some variation of this formula.
To set things up, place the coordinates of A through D in four rows like this
A = (-2,3)
B = (3,3)
C = (5,8)
D = (0,8)
Let's delete the labels
(-2,3)
(3,3)
(5,8)
(0,8)
Afterward, we make a copy of the first point (-2,3) and place it at the bottom of the list
(-2,3)
(3,3)
(5,8)
(0,8)
(-2,3)
This will help the list form a loop.
Let's space out the x and y coordinates

After that is set up, draw the diagonals shown here

We multiply along the red diagonal pairs and add up those products
-2*3+3*8+5*8+0*3 = -6+24+40+0 = 58
Do the same for the blue diagonal pairs as well
-2*8+0*8+5*3+3*3 = -16+0+15+9 = 8
Subtract the results
58 - 8 = 50
If this result was negative, then we'd take the absolute value of it to ensure it's positive.
Lastly, take half of this to get the area = (1/2)*50 = 25
The final answer to problem 1 is 25 square units.
A word of caution:
If you swap the positions of B and C, then the shoelace formula will yield an area of 0.
It's a strangely fascinating situation where one half of the area cancels out with the other half (it forms a bow-tie shaped figure).

vs

-----------------------------------------
Some more practice
https://www.algebra.com/algebra/homework/Points-lines-and-rays/Points-lines-and-rays.faq.question.1197252.html
Answer by greenestamps(13209)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The response from the other tutor says to use a magical formula for the area of a parallelogram in terms of the coordinates of the vertices.
That is a good method if all you want to do is to get the answers without learning anything.
In every one of these examples, one pair of sides is either horizontal or vertical, so you can find the area in each case using the basic formula,
Area = base * height
I will get you started on a couple of your examples.
2. (-2, 7), (-4, 4), (-11, 4), and (-9, 7)
(-2,7) and (-9,7) determine a horizontal segment of length 7; (-4,4) and (-11,4) determine another horizontal segment of length 7. The vertical distance between those two horizontal segments is the difference between 4 and 7, which is 3. So the area is 7*3 = 21.
3. (-6, 6), (-6, 3), (-12, 3), and (-12, 6)
(-6,6) and (-6,3) determine a vertical segment of length 3; (-12,3) and (-12,6) determine another vertical segment of length 3. The horizontal distance between those two vertical segments is the difference between -6 and -12, which is -6. So the area is 3*6 = 18. Note that this parallelogram is in fact a rectangle.
Work the other examples by the same process.
Answer by erinonimus(2)  (Show Source): (Show Source):
You can put this solution on YOUR website! 1. (-2, 3), (5, 8), (3, 3), and (0, 8)
Let
A (-2,3)
B (5,8)
C (3,3)
D (0,8)
Area of parallelogram = (b1−a1)(d2−a2)−(b2−a2)(d1−a1)
Therefore,
=(5-(-2))(8-3)-(8-3)(0-(-2))
=(5+2)(8-3)-(8-3)(0+2)
=(7)(5)-(5)(2)
=35-10
=25 sq. units
E. 25 sq units
Apply the same formula to the rest of the questions
Question 1203601: There are two windows in Elana's bedroom, each of which has four
right angles. One of her windows has four congruent sides. The other
window contains two pairs of opposite sides that are equal, but all
four sides are not congruent. Which statement about Elana's
windows is true?
A. Both windows are squares
B. Both windows are pentagons
C. Both windows are rectangles
D. Both windows are rhombuses.
Found 3 solutions by math_tutor2020, ikleyn, MathLover1:
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Window A:- 4 right angles
- 4 congruent sides
Window A is a square.
Any square is also a rectangle (but not the other way around).
A square is a specific type of rectangle where all sides are the same length.
Window B:- 4 right angles
- 2 pairs of opposite sides congruent, but all 4 sides are not congruent
Therefore, window B is a non-square rectangle (i.e. it is wider than it is tall, or it is taller than it is wide). Example: a 4 by 5 rectangle
Answer: Both windows are rectangles
Answer by ikleyn(52878)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Reasoning in the post by @MathLover1 is long, but incorrect.
Her answer is incorrect, too.
The correct answer is "C. Both windows are rectangles".
It is so clear, that I hesitate to spend your time explaining.
It is the same as to explain why 2 x 2 is 4, but not 73.
Answer by MathLover1(20850)   (Show Source): (Show Source):
Question 1203482: the three vertices of a parallelogram are (1,3);(0,0);(4,0) Find the three possible locations of the fourth vortex
Found 2 solutions by ikleyn, MathLover1:
Answer by ikleyn(52878)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
the three vertices of a parallelogram are (1,3);(0,0);(4,0) Find the three possible locations of the fourth  vertex. vertex.
~~~~~~~~~~~~~~~~~~~~~~
Surely, in this problem the major step and the major part
is to guess dispositions of these three parallelograms
and represent them. It is done in Figures 1, 2 and 3 below.
The 4th vertex is shown by red circle in each Figure, together with its coordinates.
As soon as the parallelograms are shown and presented, finding
the coordinates of the added 4th vertex is just a boring routine elementary procedure.
 Figure 1. Fourth vertex is (5,3)
Figure 1. Fourth vertex is (5,3)
 Figure 2. Fourth vertex is (-3,3)
Figure 2. Fourth vertex is (-3,3)
 Figure 3. Fourth vertex is (3,-3)
Figure 3. Fourth vertex is (3,-3)
Solved and answered in full, with illustrations.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! the three vertices of a parallelogram are
( , , ) )
( , , ) )
( , , ) )
Find the three possible locations of the fourth vortex
a parallelogram is a figure with opposite sides parallel
the fourth vortex is ( , ,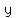 ) )
line that passes through (  , , ) and ( ) and (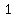 , , ) is parallel to line that passes through ( ) is parallel to line that passes through ( , , ) and ( ) and ( , , ) )
so, find a slope of the line that passes through ( , , ) and ( ) and (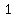 , , ) : ) :

parallel lines have same slope, so line that passes through (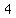 ) and ( ) and (  , ,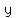 ) will be ) will be
 ..use point ( ..use point ( , , ) )


now, we know that point ( , , ) will be intersection of tis line and a line that passes through ( ) will be intersection of tis line and a line that passes through ( , , ) and is parallel to x-axis, or a line ) and is parallel to x-axis, or a line 




and


( , , ) = ( ) = ( , , ) )

Question 1202080: Given: m < OHE = 4q
m < HER = 2q
Find: a) value of q
b) m < OHE
c) m < HER
Found 3 solutions by greenestamps, ikleyn, mananth:
Answer by greenestamps(13209)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Although the presentation of the problem is poor, with the chosen title of "parallelograms" for the post, it is clear that angles OHE and HER are adjacent angles in a parallelogram.
Then, since adjacent angles in a parallelogram are supplementary...
4q+2q = 180
6q = 180
q = 30
ANSWERS:
a) q = 30
b) OHE = 4q = 120
c) HER = 2q = 60
Answer by ikleyn(52878)   (Show Source): (Show Source):
Answer by mananth(16946)   (Show Source): (Show Source):
Question 1201452: Give the genus of the object: A strainer
Found 2 solutions by ikleyn, josgarithmetic:
Answer by ikleyn(52878)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
From this source: https://en.wikipedia.org/wiki/Genus_(mathematics)
In mathematics, genus (plural genera) has a few different, but closely related, meanings.
Intuitively, the genus is the number of "holes" of a surface. A sphere has genus 0, while a torus has genus 1.
If your question has different meaning, then take a labor to decipher it . . .
Answer by josgarithmetic(39630)  (Show Source): (Show Source):
Question 1201451: The shape of a barbeque pit is like a parallelogram with the height of 54 in and a base of 60 in. It cost $0.20 per ft2 to fill the pit with charcoals. How is the total cost
Answer by ikleyn(52878)   (Show Source): (Show Source):
Question 1201336: find the measure of the four angles of parrallelogram next if m
Answer by greenestamps(13209)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Angles N and T are adjacent angles in the parallelogram, so the sum of their measures is 180 degrees.
(3x-10)+(2x+20) = 180
Solve using basic algebra....
Question 1200930: Two consecutive angles of a parallelogram are in the ratio 43:47. How many degrees are there in each angle of the parallelogram?
Answer by ikleyn(52878)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
So the angles are 43x and 47x, giving the sum of 43x + 47x = 90x,
where x is some, now unknown, common measure of the angles.
The sum of two consecutive angles in any parallelogram is 180 degrees, so
90x = 180, giving x = 180/90 = 2 degrees.
Thus the angles are 2*43 = 86 degrees and 2*47 = 94 degrees. ANSWER
Solved.
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160
|






