Question 651362: how to multiple, divide, add and subtract numbers with different signs
Answer by MathLover1(20850)   (Show Source):
You can put this solution on YOUR website!
there are 4 possibilities:
+ +
Nothing new here, just add as usual.
+ -
You are going to the right and then to the left, so they are fighting with each other, and you don't get very far. Ignore the signs and subtract the bigger one minus the smaller one. The bigger one wins out as far as which direction you are going, so it determines the sign of your answer.
- +
You are going to the left and then to the right, so again they are fighting, so just like in the last case, you ignore the signs and subtract the bigger one minus the smaller one and the bigger one wins and determines the sign of your answer.
- -
Now you are going to the left and then going to the left again, so to determine how far you are going you ignore the signs and add, and since you will end up to the left of  , the sign of your answer will be negative.
or, simple:
Like Signs - Add and the sign is the common sign.
Different Signs - Subtract and use the sign of the bigger one.
Our original subtraction of positive numbers like 7-5 can be take care of by adding a negative, since 7+-5 give the same answer as 7-5, so we can generalize this to a definition for subtracting any two signed numbers. So to subtract two signed numbers you change it into an addition problem by changing the second number to its opposite.
To subtract, change the sign of the second number and add. And that's really all there is to it. You just have to remember to do it, and that takes practice.
combinations of plus and minus for multiplication of signed numbers:
+ +
No negative numbers here, so nothing new.
+ -
Multiplying by positive numbers means repeated addition, so the same thing should be true when you multiply it by a negative number. The repeated addition of a negative number gives a negative number and the absolute value, that is the size without the minus sign, is simply the product of the two absolute values. This means when you multiply a positive number times a negative number, you multiply the two numbers ignoring the signs, and the sign of the answer is negative.
- +
We want multiplication to be commutative, so this should be done the same way as +-.
- -
This one is slightly trickier to understand, and I've never seen a convincing physical interpretation of it. Mainly you have to accept this on the basis that it is the only mathematically consistent way to define it given the other definitions. There are a number of ways to think about it. If -+ is - then -- somehow has to be something different, so it must be +. Or you can think of it as, since -+ is - then multiplying by a minus must change the sign, so in a minus times a minus the first minus must change the sign of the second one to plus. An interesting more formal way of seeing it is to use the distributive property. Take an example with numbers to make it friendlier.
 ,
but also by the distributive property
So whatever 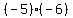 is, when you add it to  you have to get , and the only thing you can add to and get is  . Anyway, however you see it, it seems that the only possible thing for the product of two negatives to be is a positive.
Again just like with addition we can make this easier to remember by collapsing it down to just two cases, and here it is really much simpler that with addition, because with multiplication you always multiply, so all you have to worry about is what the sign of the answer will be.
Always multiply
Like signs, sign is +
Different signs, sign is
The same rules about signs hold for division as for multiplication. Also if you have a problem that is all multiplication and division, you can just ignore the signs and then figure out what the sign of the answer is by counting up the minuses and if it is even the answer is plus and if it is odd the answer is minus. But be careful, you can only do this if the problem is all multiplication and division.
|
|
|
