Question 485329: prove that, square root of 2 is not a rational number.
Found 2 solutions by richard1234, MathLover1:
Answer by richard1234(7193)   (Show Source): (Show Source):
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The proof that  is is 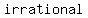 : :
Let's 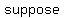  were a were a  number. Then we can write it number. Then we can write it  where where  , ,  are are  numbers, numbers,   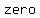 . .
We additionally make it so that this  is simplified to the lowest terms, since that can obviously be done with any fraction. is simplified to the lowest terms, since that can obviously be done with any fraction.
It follows that  , or , or  . So the square of . So the square of  is an is an   since it is since it is  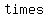 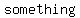 . .
From this we can know that  itself is also an itself is also an  number. Why? Because it can't be number. Why? Because it can't be  ; if ; if  itself was itself was  , then , then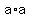 would be would be  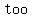 . Odd number times odd number is always odd. . Odd number times odd number is always odd.
-if  itself is an itself is an  number, then number, then  is is  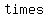 some other whole number, or some other whole number, or  where where  is this other number. We don't need to know exactly what is this other number. We don't need to know exactly what  is; it won't matter. Soon is coming the is; it won't matter. Soon is coming the 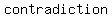 : :
If we substitute  into the original equation into the original equation  , this is what we get: , this is what we get:




This means  is is  , from which follows again that , from which follows again that  itself is an itself is an  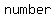 ! !
WHY is that a 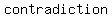 ? Because we started the whole process saying that ? Because we started the whole process saying that  is simplified to the lowest terms, and now it turns out that is simplified to the lowest terms, and now it turns out that  and and  would would 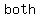 be be  . So . So  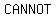 be be  . .
conclusion:  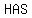 to be to be 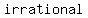 . .
|
|
|