Question 1183754: The sum of two whole number is 45 and their difference is less than 10. what is the number of possible pair
Found 3 solutions by josgarithmetic, ikleyn, greenestamps:
Answer by josgarithmetic(39620)   (Show Source):
Answer by ikleyn(52806)  (Show Source):
You can put this solution on YOUR website! .
The sum of two whole number is 45 and their difference is less than 10. what is the number of possible pair
~~~~~~~~~~~~~~~~~~~~
You are given a system, consisting of one equation and one inequality
x + y = 45 (1)
x - y < 10 (2)
where x and y are whole numbers.
Let solve the problem graphically to make the solution visible.
The figure below shows the line x + y = 45 (red line) and line y = x - 10 (green line).
The solution set for the system (1), (2) is the set of integer points on the red line, that are ABOVE the green line.
Plot x + y = 45 (red), y = x -10 (green)
You can count these points manually.
Their number is (a) 28, if the zero is admitted for x as a whole number,
or (b) 27, if the zero is NOT admitted for x as a whole number.
The set of solutions is (0,45), (1,44), (2,43), (3,42), . . . , (27,18) in case (a) (28 pairs)
or (1,44), (2,43), (3,42), . . . , (27,18) in case (b) (27 pairs)
Solved.
-------------
I do not agree with the @greenestamps comment regarding my solution,
as well as I do not agree with his solution.
@greenestamps actually solved another problem, which says
The sum of two whole number is 45 and their distance on the number line is less than 10.
What is the number of possible pair ?
In my post, I solved the problem CORRECTLY and exactly as it was formulated/worded in the post.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
Both of the solutions in this thread are deficient.
In one of them, the equation and inequality are shown, and nothing is said about how to solve the pair to get the answer to the problem. And following their suggestion can get you into trouble if you aren't careful.
So that response is of little help to the student.
In the other response, the statement that x-y<10 means x is the larger of the two whole numbers, which makes most of the pairs she shows in her response invalid.
So that response ends up with the wrong answer.
The question itself is easily solved informally.
(1) Start with the two whole numbers with a sum of 45 whose difference is as small as possible: 23 and 22.
(2) Then add 1 to one of the numbers and subtract 1 from the other to get another pair; then continue until the difference between the two numbers is greater 10 or greater. You end up with
(23,22) (24,21) (25,20) (26,19) (27,18)
That's 5 pairs.
ANSWER: 5 pairs
Note the statement of the problem does not make it clear whether or not the "pairs" are ordered. If the pairs are ordered, then of course the answer is 10 pairs instead of 5.
A formal solution to the problem might go like this.
Let the two whole numbers be x and 45-x.
The difference between the two numbers is less than 10:
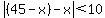
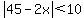
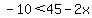 and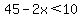 
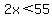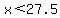 and 
 and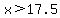 
Given that the two numbers are whole numbers, the solution set is 
That gives 10 (ordered) pairs, or 5 different unordered pairs.
|
|
|
