Question 943508: How many 3- digit even numbers are there that have 24 as the sum of their digits?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! THE SECOND GRADER ANSWER (we do not even need a fifth grader here):
If the sum is 24, no digit can be zero,
because the sum of the other two digits can be at most 9+9=18<24.
In fact, no digit could even be less than 5,
because that would make the sum less than 5+9+9=23.
If the number is even, the last digit must be even,
and adding the requirement of being more than 5,
it has to be 6 or 8.
IF the last digit is 6,
the other two digits must be 9,
because 6+x+y=24 means that x+y=24-6, which means x+y=18.
So the only choice is 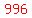 . .
IF the last digit is 8,
the other two digits must add up to 24-8=16.
The choices are
8+8=16, which would give us the number  , and , and
7+9=16, which gives us 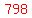 and and 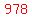 . .
How many number could we make?
Let me count them.
We made  numbers that numbers that
had 3 digits,
were even, and
their digits added to 24.
|
|
|