Question 938084: Divide 46 into two parts such that the sum of the quotients obtained by dividing one part by 7 and the other part by 3may be equal to 10.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let  and and  be the two parts of be the two parts of 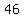 . .

The quotients (if there is no remainder) would be
 and and  such that such that
 ---> ---> 
So, we have the system of linear equations
 --> --> --> --> --> --> --> --> --> --> --> --> --> --> --> --> --> -->
NOTE: If the divisions have a quotient and a remainder,
the problem gets complicated.
We would have positive integer quotients  and and 
and positive integer remainders  and and  . .
The two parts of 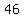 would be would be
 with with  , so , so  = 1, or 2, or 3, or 4, or 5, or 6, and = 1, or 2, or 3, or 4, or 5, or 6, and
 with with  , so , so  = 1, or 2. = 1, or 2.
Then  and and  ---> ---> . .
We would solve  to get to get
 . .
For {{a}} and  to be integers, with to be integers, with  , ,
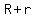 must be a multiple of must be a multiple of 
If  it must be it must be
 ---> --->  ---> ---> 
If  it could be it could be
 ---> --->  ---> --->  , or , or
 ---> --->  ---> ---> 
|
|
|