Question 714806: Find a natural number for which if we move the first digit to the last place, the number that will emerge will be half of the original.
ex 321 goes to 213 but no a sollution
Found 2 solutions by Edwin McCravy, KMST:
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Two solutions shown here. I believe there is an infinite number, but I don't know how to prove it yet.
105,263,157,894,736,842 turns into 052,631,578,947,368,421 when you move the first digit to the end.
(No one said that the second digit could not be zero).
210,526,315,789,473,684 turns into 105,263,157,894,736,842
HOW I FOUND SOLUTIONS:
Let  be the first digit be the first digit
The number will be 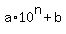 where where  is another natural number is another natural number
Moving the first digit to the end yields the number 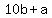
 --> -->  --> -->  --> -->  --> --> 
Obviously,  cannot be a multiple of 19, cannot be a multiple of 19,
so 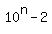 must be a multiple of 19. must be a multiple of 19.
 where where  is another natural number is another natural number
 --> --> 
Computer and calculator did not help, so I took paper and pencil.
I started dividing 1 divided by 19.
I knew it would be a repeating decimal, and I only needed to get to the 18th digit.
I was looking for a remainder of 2.
I got to
 and the remainder digit was 2. and the remainder digit was 2.
Multiplying it all by 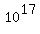 we get we get
 with a remainder of 2, with a remainder of 2,
which means 
So I found my 
 substituted into substituted into  means means
 --> --> 
The solutions shown above come from  and and  . .
|
|
|