Take a number, x. If it adds to some other number to equal 150, then 150-x is that other number.
We have x and 150-x, and their product must be as large as possible.
Graph it, or remember that it will be a parabola opening down.
Thus, when its derivative equals 0 
the function has its maximum.
Subtract 150 from both sides.
Divide both sides by -2
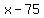
The product of the numbers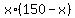 
has its maximum value when x=75. And when x=75 then 150-x = 150-75 = 75.
The two numbers are 75.
You could also solve this by looking at a much smaller number, like 6.
What two real numbers whose sum is 6 have the maximum product?
Compare 3 and 3 with 1 and 5 with 4 and 2 with 6 and 0. The largest product is 3*3.
Look at 5. The largest product comes from 2.5 * 2.5
For 8 the largest product comes from 4*4.
By observation you can see that when the sum is a positive number, then the largest product comes from the number divided by 2.
150/2=75.
If you need help understanding math so you can solve these problems yourself, then one on one online tutoring is the answer ($30/hr). If you need faster solutions with guaranteed detailed answers, then go with personal problem solving ($3.50-$5.50 per problem). Contact me at fcabanski@hotmail.com
(