Does "3^3^3" or  mean
mean  or
or 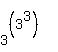 ?
I will assume it's
?
I will assume it's 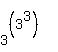 ; otherwise we'd just do it with the calculator
; otherwise we'd just do it with the calculator
 and the answer would obviously be 3.
So I assume you mean:
and the answer would obviously be 3.
So I assume you mean:
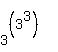 30 = 1
31 = 3
32 = 9
33 = 27
34 = 81
35 = 243
36 = 729
37 = 2187
We can see that the last digits repeat in cycles of 4: 1,3,5,7,1,3,5,7,...
So the last digit of
30 = 1
31 = 3
32 = 9
33 = 27
34 = 81
35 = 243
36 = 729
37 = 2187
We can see that the last digits repeat in cycles of 4: 1,3,5,7,1,3,5,7,...
So the last digit of 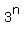 is the same as the last digit of n mod 4.
Therefore since
is the same as the last digit of n mod 4.
Therefore since 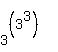 is the same as
is the same as 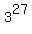 , and since 27 mod 4 = 3,
the last digit of it is the same as the last digit of
, and since 27 mod 4 = 3,
the last digit of it is the same as the last digit of  , so the answer is 7.
Edwin
, so the answer is 7.
Edwin