Question 1012016: The sum of 6 consecutive odd numbers is 132. What is the sum of all the tens digits of these numbers?
Found 2 solutions by ikleyn, KMST:
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let x be the smallest of these numbers.
Then the numbers are x, x+2, x+4, x+6, x+8 and x+10.
Their sum is 6x + 30.
Hence,
6x + 30 = 132,
6x = 132-30 = 102.
x = 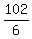 = 17. = 17.
The numbers are 17, 19, 21, 23, 25, 27.
The rest is on you.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Six consecutive odd numbers (or six consecutive even numbers)
could be represented by
 , ,  , , 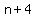 , , 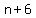 , , 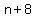 , and , and 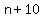 . .
The sum would be

In this case,
 --> --> --> --> --> --> --> --> . .
So the numbers are 17, 19, 21, 23, 25, and 27.
The sum of all the tens digits is
 . .
Another way:
If the sum is  , the average is , the average is  . .
Consecutive odd integers form an arithmetic sequence,
and in an arithmetic sequence, the average (or mean) is also the median.
That means that  of the 6 consecutive odd numbers are more than of the 6 consecutive odd numbers are more than  , with a , with a  for a tens digit, for a tens digit,
and the other  are less than are less than  , including , including   and and  . .
So  of the six odd numbers have a of the six odd numbers have a  as a tens digit, and the other as a tens digit, and the other  have a have a  as the tens digit. as the tens digit.
So the sum of the tens digits is
 . .
|
|
|