Tutors Answer Your Questions about Numbers Word Problems (FREE)
Question 1210416: The water park is a popular field trip destination. This year the senior class at High School A and
the senior class at High School B both planned trips there. The senior class at High School A
rented and filled 10 vans and 8 buses with 394 students. High School B rented and filled 5 vans
and 10 buses with 365 students. Every van had the same number of students in it as did the
buses. Find the number of students in each van and in each bus.
Answer by ikleyn(52878)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The water park is a popular field trip destination. This year the senior class at High School A and
the senior class at High School B both planned trips there. The senior class at High School A
rented and filled 10 vans and 8 buses with 394 students. High School B rented and filled 5 vans
and 10 buses with 365 students. Every van had the same number of students in it as did the
buses. Find the number of students in each van and in each bus.
~~~~~~~~~~~~~~~~~~~~~~~~~~
Let x be the number of students per van, and
let y be the number of students per bus.
Write equations as you read the problem
10x + 8y = 394, (1)
5x + 10y = 365. (2)
Solve the system by the Elimination method.
For it, multiply equation (2) by 2 (both sides). Keep equation (1) as is
10x + 8y = 394, (1')
10x + 20y = 730. (2')
From equation (2') subtract equation (1'). You will get
20y - 8y = 730 - 394,
12y = 336
y = 436/12 = 28.
Now from equation (1) find x, substituting x = 28 there
10x + 8*28 = 394,
10x = 394 - 8*28 = 170,
x = 170/10 = 17.
ANSWER. 17 students in each van and 28 students in each bus.
Solved.
Question 1210350: What plus -1 equals -20
Found 2 solutions by ikleyn, AnlytcPhil:
Answer by ikleyn(52878)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Informally, when you add -1 to a number, you shift the number one unit to the left on the number line.
So, if your shifted number is -20 after adding -1, it means that your original number was -19.
Thus, -19 is your answer in this problem.
Answer by AnlytcPhil(1808)   (Show Source): (Show Source):
You can put this solution on YOUR website!
What plus -1 equals -20?
Let the answer be x:
x + (-1) = -20
Add (+1) to both sides of the equation):
x + (-1) + (+1) = -20 + (+1)
x = -20 + 1
x = -19
The answer is -19.
Edwin
Question 1210340: What numbers add to make 10 and times to make -16
Found 2 solutions by josgarithmetic, greenestamps:
Answer by josgarithmetic(39630)  (Show Source): (Show Source):
Answer by greenestamps(13209)   (Show Source): (Show Source):
Question 1180063: In the last two times around the game board, Wendell thought he was a goner. First, he had to pay ½ of his money in rent to somebody. He then had to pay $25 because of a “Chance” card. After that, he landed on another property where he had to pay 3/5 of his remaining money in rent. Fortunately, on his next turn he passed “Go” and collected $200. However, he landed on a property that wacked him for ½ of his money. Next, he got a “Chance” card and landed in jail. After he paid $50 to get out, the poor guy only had $70 cash left - no property, no nothing. How much money did he have at the beginning of this narrative?
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to solve this problem by working backward:
1. **Jail:** Before paying $50 to get out of jail, Wendell had $70 + $50 = $120.
2. **Half Money Rent:** Before losing half his money to rent, he had $120 * 2 = $240.
3. **Passed Go:** Before collecting $200, he had $240 - $200 = $40.
4. **3/5 Rent:** Before paying 3/5 of his money in rent, he had $40 / (1 - 3/5) = $40 / (2/5) = $100.
5. **Chance Card:** Before paying $25, he had $100 + $25 = $125.
6. **Half Money Rent:** Before losing half his money to rent, he had $125 * 2 = $250.
**Answer:** Wendell had $250 at the beginning of the narrative.
Question 1186061: At the Yellow Golf Tournament, the leaderboard shows Anna's score as 11 on the front nine and 81 on the back nine. What was Anna's total score for the rounds?
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Anna's total score is the sum of her front nine and back nine scores:
11 + 81 = 92
Anna's total score for the round was $\boxed{92}$.
Question 1209434: A, B and C are distinct digits and 4 * AB = CA. Find the sum A+B+C
Found 3 solutions by greenestamps, MathTherapy, ikleyn:
Answer by greenestamps(13209)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A, B, and C are distinct digits and 4* AB = CA.
The given multiplication puts two restrictions on the choice for digit A:
(1) 4 * AB gives a result with units digit A. 4 times any integer yields an even product, so A must be even.
(2) 4 * AB gives a result that is a 2-digit integer. That means A must be no greater than 2.
Those two conditions together mean A must be 2.
Now 4 * AB yields a product with units digit 2, so be can only be either 3 or 8.
But 4 * 28 yields a product of 3 digits, so B must be 3.
So we have that the indicated multiplication must be 4 * 23 = 92.
So A = 2, B = 3, and C = 9.
ANSWER: A+B+C = 2+3+9 = 14
Answer by MathTherapy(10556)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A, B and C are distinct digits and 4 * AB = CA. Find the sum A+B+C
4AB = CA
Obviously, AB and CA are 2-digit numbers
As such. AB = 10A + B, and CA = 10C + A. So, 4AB = CA becomes:
4(10A + B) = 10C + A
40A + 4B = 10C + A
4B = 10C + A - 40A
4B = 10C - 39A
B = 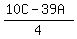 Now, we can see that C - 39A is a MULTIPLE of 4, so A CANNOT be an ODD DIGIT. Furthermore, the digit A MUST be less than 3,
as ANY digit greater than 3 would yield a negative (< 0) numerator. And, neither can digit A be 0 because, while the units
digit in CA can be 0, the tens digit in AB CANNOT.
Having said that, digit A being less than 3, not ODD, and NOT 0 makes it 2
B =
Now, we can see that C - 39A is a MULTIPLE of 4, so A CANNOT be an ODD DIGIT. Furthermore, the digit A MUST be less than 3,
as ANY digit greater than 3 would yield a negative (< 0) numerator. And, neither can digit A be 0 because, while the units
digit in CA can be 0, the tens digit in AB CANNOT.
Having said that, digit A being less than 3, not ODD, and NOT 0 makes it 2
B = 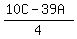 B =
B = 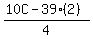 ----- Substituting 2 for A
B = ----- Substituting 2 for A
B =  At this point, 10C MUST be greater than 78, which means that C can be 8 or 9. But, if C = 8, then numerator becomes 2, and 2 is
NOT a MULTIPLE of 4. So, C MUST be 9
B =
At this point, 10C MUST be greater than 78, which means that C can be 8 or 9. But, if C = 8, then numerator becomes 2, and 2 is
NOT a MULTIPLE of 4. So, C MUST be 9
B = 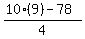 ------ Substituting 9 for C
B = ------ Substituting 9 for C
B = 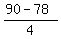 B =
B =  B = 3
Therefore, (A, B, C) = (2, 3, 9), and A + B + C = 2 + 3 + 9 = 14
You can do the CHECK!!
B = 3
Therefore, (A, B, C) = (2, 3, 9), and A + B + C = 2 + 3 + 9 = 14
You can do the CHECK!!
Answer by ikleyn(52878)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A, B and C are distinct digits and 4 * AB = CA. Find the sum A+B+C
~~~~~~~~~~~~~~~~~~~~~
Since 4 * AB = CA, CA must be a two-digit number >= 40. (*)
Since 4 * AB = CA, we conclude that AB is a two-digit number between 10 and 24, inclusive.
So, A is either 1 or 2. But from 4 * AB = CA, digit A must be even - so,
we conclude that A = 2.
Thus, CA is a two digit number multiple of 4 and with the last digit 2.
Such numbers CA can be only 12, 32, 52, 72, 92.
Condition (*) prohibits 12 and 32, so the remaining opportunities for CA are 52, 72, 92.
Divide CA by 4, and you will get the values 13, 18, 23 for AB.
But, as we established above, the digit A is 2; therefore, AB can only be 23.
Thus, A = 2; B = 3; C = 9. All these digits are different.
The sum A + B + C is 2 + 3 + 9 = 14. ANSWER
Solved.
Question 1209092: The difference of two positive numbers is 9. What is the minimum sum of their squares?
Absolute extrema/optimization
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52878)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The difference of two positive numbers is 9. What is the minimum sum of their squares?
Absolute extrema/optimization
~~~~~~~~~~~~~~~~~~~~~
Let x be a greater of these two real numbers; y be a smaller of these two real numbers.
Then x - y = 9, or x = y+9.
They want you find the minimum of  , which is , which is
 = = 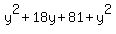 = = 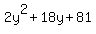 .
So, actually, we want to find the minimum of this quadratic function
f(y) = .
So, actually, we want to find the minimum of this quadratic function
f(y) = 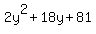 on the set of positive real numbers y > 0.
The global minimum of a quadratic function of the general form f(y) = ay^2 + by + c with positive
leading coefficient "a" is achieved at on the set of positive real numbers y > 0.
The global minimum of a quadratic function of the general form f(y) = ay^2 + by + c with positive
leading coefficient "a" is achieved at 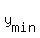 = =  . In this case . In this case
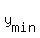 = = 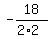 = -4.5,
which is negative value out of the scope of our consideration.
In the area y > 0, we have the ascending branch of the parabola on the right from its minimum in negative
number. Had we consider the scope of non-negative real numbers y >= 0, then the minimum of the parabola
f(y) = = -4.5,
which is negative value out of the scope of our consideration.
In the area y > 0, we have the ascending branch of the parabola on the right from its minimum in negative
number. Had we consider the scope of non-negative real numbers y >= 0, then the minimum of the parabola
f(y) = 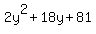 would be at y = 0 with the value f(0) = 81.
But, according to the problem, our scope is the set of positive numbers y > 0, and in this domain,
quadratic function f(y) = would be at y = 0 with the value f(0) = 81.
But, according to the problem, our scope is the set of positive numbers y > 0, and in this domain,
quadratic function f(y) = 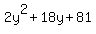 does not have the minimum, at all.
ANSWER. In the set of positive numbers, the function does not have the minimum, at all.
ANSWER. In the set of positive numbers, the function  with the restriction x-y = 9 has no minimum. with the restriction x-y = 9 has no minimum.
Solved.
---------------------
Above, I told you the whole story with all details.
I could explain everything in more short terms, simply noticing that
the parabola f(y) = 2y^2 + 18y + 81 has two positive terms 2y^2 and 18y
in the domain y > 0.
So, the values of f(y) go up as "y" goes to the right from zero,
which means that function f(y) raises there.
In opposite, function f(y) goes down as "y" approaches 0 from the right side.
But "y" never gets 0 in the positive domain - so we never get the minimum of f(y)
in the positive domain y > 0.
With these two explanations, you have now a complete picture and a complete vision to the problem.
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Let m and n be the mystery numbers where m > n.
Both are positive.
There's a 9 unit gap between them to indicate m-n = 9 which can be rearranged to m = n+9.
p = m^2+n^2 = summing their squares
The goal is to make p as small as possible.
To do so, we need to make n as small as possible.
If n = 0, then m = n+9 = 0+9 = 9 and m^2+n^2 = 0^2+9^2 = 81
But n = 0 isn't allowed since n > 0.
If n approaches 0 from above, then m^2+n^2 approaches 81 from above.
Therefore, m^2+n^2 doesn't have a minimum.
We have asymptotic behavior going on.
A similar situation is to think of the graph y = 1/x
As x gets bigger, y approaches 0 but never actually gets there.
--------------------------------------------------------------------------
Summary: There is no minimum sum of the squares.
The sum of squares gets closer to 81 from above, but never actually arrives at this sum itself.
Question 1208831: Evan thinks of two numbers. If he adds 2 to the first number and then multiplies the sum by three, the result is the second number. if he subtracts 3 times the first number from the second number, the result is 8, what are the numbers?
Found 3 solutions by greenestamps, MathTherapy, josgarithmetic:
Answer by greenestamps(13209)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Let the first number be x and the second be y.
If he adds 2 to the first number and then multiplies the sum by three, the result is the second number: y=3(x+2)=3x+6
If he subtracts 3 times the first number from the second number, the result is 8: y-3x=8 --> y=3x+8
We now have two expressions for y in terms of x, so those two expressions must be equal: 3x+6 = 3x+8
That equation clearly has no solutions.
ANSWER: no solution
Answer by MathTherapy(10556)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Evan thinks of two numbers. If he adds 2 to the first number and then multiplies the sum by three, the result is the second number. if he subtracts 3 times the first number from the second number, the result is 8, what are the numbers?
No such numbers!
Let 1st number be F, and 2nd, S
Then we get: 3(F + 2) = S____3F + 6 = S ------ eq (i)
Also, S - 3F = 8 ----- eq (ii)
3F + 6 - 3F = 8 ----- Substituting 3F + 6 for S in eq (ii)
3F - 3F = 2
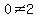 , and therefore, there are NO SOLUTIONS!! , and therefore, there are NO SOLUTIONS!!
Answer by josgarithmetic(39630)  (Show Source): (Show Source):
Question 1208708: The pages in a book are numbered from 1 to 2710. How many times was the digit 7 printed?
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
You can put this solution on YOUR website!
We will count the 7s among the thousands place digits,
then the hundreds place digits, then the tens place digits,
and finally the one-place digits.
There are no 7's among the thousands place digits.
Among the hundreds place digits,
700-799 account for 100 hundreds place 7s,
1700-1799 account for 100 hundreds place 7s,
2700-2710 account for 11 hundreds place 7s
That's 211 7s among the hundredths place digits.
70-79 account for 10 tens place 7s
170-79 account for 10 tens place 7s
...
2670-2679 account for 10 tens place 7s
That's 27x10=270 7s among the tens place digits.
[Note: from 2680 through 2710 there are no 7s in tens places.]
The 7s in ones digits occur in 7,17,27,37,...2697,2707
That's an arithmetic sequence with a1=7, an=2707, d=10
We find the number of terms:




 Sum total= 211+270+271=752
There are 752 7s in all the page numbers.
Edwin
Sum total= 211+270+271=752
There are 752 7s in all the page numbers.
Edwin
Question 1208442: Four times a certain number is equal to the number substracted from 40. Find the number
Found 2 solutions by MathTherapy, josgarithmetic:
Answer by MathTherapy(10556)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Four times a certain number is equal to the number substracted from 40. Find the number
Is this dude really SERIOUS? Why does the problem refer to a certain number throughout, yet he
decides to assign 2 DIFFERENT variables (p and n) to that VERY SAME number? That is truly one of the
mist RIDICULOUS things I've ever seen. Plus, as a supposed "tutor," why would he spell forty as FOURTY?
Do these people need spellcheck for every single word they type? And, what's the sense in spelling/misspelling
40 when you can just write "40?"
I really feel sorry for the person who asked for help. How is he/she going to be able to find that certain number
with the following equation: 4p = 40 - n, or 4p = FOURTY - n?
p, the certain number
4p, four times a certain number
4p=, four times a certain number is equal to....
40-n, the certain number subtracted from fourty
Answer by josgarithmetic(39630)  (Show Source): (Show Source):
You can put this solution on YOUR website! p, the certain number
4p, four times a certain number
4p=, four times a certain number is equal to....
40-p, the certain number subtracted from fourty
Question 1208616: Find the two-digit consecutive prime numbers that have the greatest difference between them.
Answer by ikleyn(52878)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
It was solved and answered at this forum many years ago. See the link
https://www.algebra.com/algebra/homework/divisibility/Divisibility_and_Prime_Numbers.faq.question.1146803.html
Question 1208603: 14 is added to 2\3 of a number. The result is 1 whole number 1\4 times the original number.find the numbers.
Found 3 solutions by Edwin McCravy, josgarithmetic, ikleyn:
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
You can put this solution on YOUR website! 14 is added to 2\3 of a number. The result is 1 whole number 1\4 times the
original number.find the numbers.
That is not grammatical. Something is wrong or missing.
Tutor Ikleyn assumed "1 whole number 1\4" meant "1 PLUS 1/4" or 5/4.
IOW, she interpreted it to mean this:
14 is added to 2/3 of a number. The result is 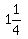 times the original number. Find the number.
With her interpretation, she obtained the answer as 24.
Notice that the student wrote "find the numbers" (plural) but she
only found only one number, and changed "numbers" to "number".
============================
Tutor josgarithmetic(39489) interpreted it as though the "1\4 times" was
reversed and should be "times 1/4". He interpreted it as:
14 is added to 2/3 of a number. The result is 1 whole number times 1/4 the
original number. Find the numbers.
He gave an example where the original number is -84 and the whole number is 2.
There are 6 solutions in all for his interpretation:
(-84,2), (-21,0), (6,12), (24,5), (42,4), (168,3)
============================
I will assume that the student inadvertently omitted the word PLUS.
So I'll do it with this interpretation:
14 is added to 2/3 of a number. The result is 1 whole number PLUS 1/4 times
the original number. Find the numbers.
Let x be the original number and let y be the 1 whole number. times the original number. Find the number.
With her interpretation, she obtained the answer as 24.
Notice that the student wrote "find the numbers" (plural) but she
only found only one number, and changed "numbers" to "number".
============================
Tutor josgarithmetic(39489) interpreted it as though the "1\4 times" was
reversed and should be "times 1/4". He interpreted it as:
14 is added to 2/3 of a number. The result is 1 whole number times 1/4 the
original number. Find the numbers.
He gave an example where the original number is -84 and the whole number is 2.
There are 6 solutions in all for his interpretation:
(-84,2), (-21,0), (6,12), (24,5), (42,4), (168,3)
============================
I will assume that the student inadvertently omitted the word PLUS.
So I'll do it with this interpretation:
14 is added to 2/3 of a number. The result is 1 whole number PLUS 1/4 times
the original number. Find the numbers.
Let x be the original number and let y be the 1 whole number.
 Solve for y, which must be a whole number:
Solve for y, which must be a whole number:



 Since y must be a whole number, x must be a multiple of 12
to cancel the denominator in the first term.
Let x = 12k
Since y must be a whole number, x must be a multiple of 12
to cancel the denominator in the first term.
Let x = 12k

 Whole numbers are non-negative integers, so
Whole numbers are non-negative integers, so


 k is an integer, so
k is an integer, so  So the infinite set of solutions is
{ (12k, 5k+14) | k > -2 }.
Some examples of solutions are:
(-24,4), (-12,9), (0,14), (12,19), (24,24), (36,29), (48,34), ...
Edwin
So the infinite set of solutions is
{ (12k, 5k+14) | k > -2 }.
Some examples of solutions are:
(-24,4), (-12,9), (0,14), (12,19), (24,24), (36,29), (48,34), ...
Edwin
Answer by josgarithmetic(39630)  (Show Source): (Show Source):
Answer by ikleyn(52878)   (Show Source): (Show Source):
Question 1208429: Find the last two digits of the number 3^123 + 7^123 + 9^123.
Found 3 solutions by ikleyn, math_tutor2020, greenestamps:
Answer by ikleyn(52878)   (Show Source): (Show Source):
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Greenestamps has a great solution. I'll provide another route.
Use the process described on this page to evaluate the following
3^123 = 27 (mod 100)
7^123 = 43 (mod 100)
9^123 = 29 (mod 100)
Each item can be verified with technology. Some examples are WolframAlpha, GeoGebra, spreadsheet, etc.
The results we got were 27, 43, and 29.
They are the last two digits of 3^123, 7^123, and 9^123 in that exact order.
Therefore, 27+43+29 = 99 are the last two digits of 3^123 + 7^123 + 9^123.
Verification with WolframAlpha
https://www.wolframalpha.com/input?i=%283%5E123+%2B+7%5E123+%2B+9%5E123%29+mod+100
Answer by greenestamps(13209)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Look for the repeating pattern of the last two digits of 3, 7, and 9 to increasing powers.
3: 03, 09, 27, 81, 43, 29, 87, 61, 83, 49, 47, 41, 23, 69, 07, 21, 63, 89, 67, 01, 03...
That pattern repeats with a cycle length of 20. 123 mod 20 = 3, so the last two digits of 3^123 is the 3rd number in the pattern: 27
7: 07, 49, 43, 01, 07...
That pattern repeats with a cycle length of 4. 123 mod 4 = 3, so the last two digits of 7^123 is the 3rd number in the pattern: 43
9: 09, 81, 29, 61, 49, 41, 69, 21, 89, 01, 09 ...
That pattern repeats with a cycle length of 10. 123 mod 10 = 3, so the last two digits of 9^123 is the 3rd number in the pattern: 29
27+43+29 = 99
ANSWER: 99
Question 1208490: 1/3 of a number is added to 5 the result is one and half times the original number find the number
Answer by ikleyn(52878)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let the unknown number be x.
Write an equation
 + 5 = 1.5x,
which is the direct translation of English to Math.
To solve, multiply both sides by 2*3 = 6
2x + 5*6 = 1.5*6*x
2x + 30 = 9x
30 = 9x - 2x
30 = 7x
x = 30/7 = 4 + 5 = 1.5x,
which is the direct translation of English to Math.
To solve, multiply both sides by 2*3 = 6
2x + 5*6 = 1.5*6*x
2x + 30 = 9x
30 = 9x - 2x
30 = 7x
x = 30/7 = 4 . ANSWER . ANSWER
Solved.
Question 1208418: 2+1
Found 2 solutions by mccravyedwin, ikleyn:
Answer by mccravyedwin(409)   (Show Source): (Show Source):
Answer by ikleyn(52878)   (Show Source): (Show Source):
Question 1208332: The car's speed decreased linearly as a function of time. The speed was 60 kph at t=1s and 40 kph at t = 5 s. Create a function that describes speed as a function of time. At what time did the car's speed equal 0?
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13209)   (Show Source): (Show Source):
You can put this solution on YOUR website!
We are told that the speed as a function of time is linear, so let's use the standard notation for a linear function: y = mx+b where the dependent variable y is the car's speed and the independent variable x is the time in seconds.
In the standard form y=mx+b, m is the slope, or rate of change. In this problem, the speed decreased from 60kph to 40kph, a change of -20kph, in 4 seconds, between t=1 and t=5. So the slope m is -20/4 = -5.
So the linear function can now be written as y=-5x+b.
Use either of the two given data points to determine the value of b. The speed is 60 at t=1:
60 = -5(1)+b
60 = -5+b
b = 65
And now we have the full linear equation: y = -5x+65
Or, in formal function notation showing speed as a function of time...
ANSWER: s(t)=-5t+65
To find when the car's speed is 0, set s(t)=0 and solve.
-5t+65 = 0
5t = 65
t = 13
ANSWER: at 13 seconds
Answer by ikleyn(52878)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The car's speed decreased linearly as a function of time.
The speed was 60 kph at t=1s and 40 kph at t = 5 s.
Create a function that describes speed as a function of time. At what time did the car's speed equal 0?
~~~~~~~~~~~~~~~~~~~~~~~~
The function is
f(t) = V - at, (1)
where V is the initial speed at t= 0, "a" is the rate of the speed decreasing, t is the time (in seconds).
We don't know V at t= 0 (it is not given), but we can easily find "a".
"a" is the ratio of the change of the speed to the elapsed time
a = 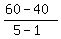 = =  = 5 kilometer per hour per second.
Now from equation (1) we will find V
V - 5*1 = 60 ,
V = 60 + 5 = 65.
Thus the function is f(t) = 65 - 5t kilometers per hour. ANSWER
To find the stop time, write this equation
V = 65 - 5t = 0.
From the equation, t = 65/5 = 13 seconds from the beginning. ANSWER = 5 kilometer per hour per second.
Now from equation (1) we will find V
V - 5*1 = 60 ,
V = 60 + 5 = 65.
Thus the function is f(t) = 65 - 5t kilometers per hour. ANSWER
To find the stop time, write this equation
V = 65 - 5t = 0.
From the equation, t = 65/5 = 13 seconds from the beginning. ANSWER
Solved, with all necessary explanations.
Question 1208334: For Problems 5-7, use f(x) = x³-3 and g(x) = 2x
5. Find (f+g)(x).
6. Evaluate f(4) and g(4).
7. Evaluate (f+g)(4).
Found 2 solutions by math_tutor2020, josgarithmetic:
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
Answer by josgarithmetic(39630)  (Show Source): (Show Source):
Question 1208333: For Problems 5-7, use f(x) = x ^ 3 - 3 and g(x) = 2 ^ x
5. Find (f+g)(x). 6
6. Evaluate f(4) and g(4).
7. Evaluate (f + g)(4)
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Problem 5
(f+g)(x) = f(x) + g(x)
(f+g)(x) = x^3-3 + 2^x
(f+g)(x) = 2^x + x^3 - 3
There's not much to do here in terms of simplification.
---------------------------------------------------------------------
Problem 6
f(x) = x^3-3
f(4) = 4^3-3
f(4) = 64-3
f(4) = 61
g(x) = 2^x
g(4) = 2^4
g(4) = 16
---------------------------------------------------------------------
Problem 7
(f+g)(x) = 2^x + x^3 - 3
(f+g)(4) = 2^4 + 4^3 - 3
(f+g)(4) = 16 + 64 - 3
(f+g)(4) = 77
Another approach.
(f+g)(x) = f(x) + g(x)
(f+g)(4) = f(4) + g(4)
(f+g)(4) = 61 + 16
(f+g)(4) = 77
Question 1208335: The dynamic pressure (P) on the wall increased with the square of the speed (s). Initially, P =s = 0. At a speed of 30, the pressure was 13.5. Which of the following functions represents pressure as a function of airspeed? A) P(s)=√6s B) P(s) = 0.015s2 C) P(s) = 1.15 D) P(s) = 0.45s
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52878)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The dynamic pressure (P) on the wall increased with the square of the speed (s).
Initially, P =s = 0. At a speed of 30, the pressure was 13.5.
Which of the following functions represents pressure as a function of airspeed?
A) P(s)=√6s B) P(s) = 0.015s2 C) P(s) = 1.15 D) P(s) = 0.45s
~~~~~~~~~~~~~~~~~~~~~~
Of the four given optional functions (A), (B), (C) and (D), only function (B)
increases with the square of the speed.
We only should to check, if this function has the assigned values
P(0) = 0 and P(30) = 13.5.
So, we substtute s= 0 into function (B), and we get P(0) = 0.015*0^2 = 0,
which corresponds to the given value.
Next, we substtute s= 30 into function (B), and we get P(30) = 0.015*30^2 = 13.5,
which corresponds to the given value, too.
Thus function (B) satisfies all imposed conditions.
So, (B) is the ANSWER.
Solved.
--------------------
The thing which embarrasses me in this problem is the fact that in the "given" part
they talk about "speed", while the question asks about "airspeed".
In true Math problem, all used conceptions must be consistent and do not to raise questions.
Therefore, in this problem, I would replace the term "speed" by the "air speed",
and the term "airspeed" by the term "air speed", too, in order for everything
be clear and do not to confuse the reader.
By the way, the term "airspeed" is not what you think.
-----------------------
By the definition, "airspeed" is "the speed of an aircraft relative to the air through which it is moving."
It is not "air speed", as you may think.
The term "airspeed" has one and only one meaning, totally different from the meaning of "air speed".
One goal of Math problems (the major goal) is to teach young students to think
and to solve Math problems correctly.
The other, auxiliary goal, is to teach young students to new conceptions and to new terminology
by introducing new conceptions carefully and using relevant terminology adequately.
So, the auxiliary goal is to teach students to speak correctly, in addition to think correctly.
As this problem is worded and printed in the post, it failed this auxiliary goal TOTALLY.
As the problem is worded in the post, it makes clear, that the composer/writer
does not know the subject and does not know terminology.
It is sad to see it.
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
Question 1208133: a digital timer counts down from 3 min to zero, one second at a time. for how many seconds does atleast one of these digits show a 5?
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13209)   (Show Source): (Show Source):
You can put this solution on YOUR website!
It appears that tutor @ikleyn solved the problem for a timer which counts down from 180 seconds to 0 seconds.
My guess is that the timer counts down from 3:00 to 0:00. In that case....
The digit for the minutes is never 5.
As the timer counts down, the digits representing the numbers of seconds repeat the same sequence in each minute, so we can count the number of times that a 5 appears as either of those digits in one minute and multiply our answer by 3 (for minutes digit 2, 1, or 0).
In each minute, the digits representing the seconds contain at least one 5 for the following numbers of seconds:
59 through 50 (10 occurrences)
45, 35, 25, 15, and 05 (5 occurrences)
Total number of times in each minute that at least one of the digits is 5: 10+5 = 15.
Number of times in 3 minutes that at least one of the digits is 5: 15*3 = 45.
ANSWER: 45
Answer by ikleyn(52878)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
a digital timer counts down from 3 min to zero, one second at a time.
for how many seconds does at least one of these digits show a 5?
~~~~~~~~~~~~~~~~~~~~~~~
(a) First (leftmost) digit is never 5.
(b) Consider the set of numbers XY5 from 1 to 180 inclusive with the last
(rightmost) digit of 5 and the middle digit Y =/=5.
These numbers are
005, 015, 025, 035, 045,  , 065, 075, 0.85, 0.95,
105, 115, 125, 135, 145, , 065, 075, 0.85, 0.95,
105, 115, 125, 135, 145,  , 165, 175.
The crossed numbers are those with 5 in the middle position.
The amount of such "survived" numbers is 9 + 7 = 16.
The counter counts/adds 1 as each such a number appears.
(c) To it, we should add appearances X5Z.
There are exactly 10 + 10 = 20 such appearances
050, 051, 052, 053, 054, 055, 056, 057, 058, 059,
150, 151, 152, 153, 154, 155, 156, 157, 158, 159.
The counter adds 1 as each such a number appears.
(d) Thus the total (the last) number on the counter at the end is the sum 16 + 20 = 36. ANSWER , 165, 175.
The crossed numbers are those with 5 in the middle position.
The amount of such "survived" numbers is 9 + 7 = 16.
The counter counts/adds 1 as each such a number appears.
(c) To it, we should add appearances X5Z.
There are exactly 10 + 10 = 20 such appearances
050, 051, 052, 053, 054, 055, 056, 057, 058, 059,
150, 151, 152, 153, 154, 155, 156, 157, 158, 159.
The counter adds 1 as each such a number appears.
(d) Thus the total (the last) number on the counter at the end is the sum 16 + 20 = 36. ANSWER
Solved.
-----------------------
What I did to solve the problem is THIS:
I separated the set of numbers, containing at least one digit "5",
in two disjoint subsets (b) and (c) in a way that the counter adds 1
at every appearance of a number from each of the two subsets.
Question 1208072: the mass of a bag of red star sugar is 20% greater than the mass of a bag of blue star sugar. However, a bag of red star sugar costs 50% more than a bag of blue star sugar. for the same mass, red star sugar costs how much percent more than blue star sugar?
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13209)   (Show Source): (Show Source):
You can put this solution on YOUR website!
"The mass of a bag of red star sugar is 20% greater than the mass of a bag of blue star sugar."
Arbitrarily, suppose the bag of red star sugar is 6kg and the bag of blue star sugar is 5kg.
"However, a bag of red star sugar costs 50% more than a bag of blue star sugar."
Arbitrarily, suppose the bag of red star sugar costs $3 and the bag of blue star sugar costs $2.
"For the same mass, red star sugar costs how much percent more than blue star sugar?"
The cost per kg of the red star sugar is $3/6kg = $0.50; the cost per kg of the blue star sugar is $2/5kg = $0.40.
The ratio of the costs per kg of the red and blue sugars is $0.50/$0.40 = 5/4 = 1.25 = 125%; so for the same mass the red star sugar costs 25% more then the blue star sugar.
Answer by ikleyn(52878)   (Show Source): (Show Source):
Question 1208029: A certain number is subtracted 4 times from twice from square of the number and the result is 70. Find the number
Answer by ikleyn(52878)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A certain number is subtracted 4 times from twice from square of the number
and the result is 70. Find the number.
~~~~~~~~~~~~~~~~~~
I edited your post in order for to make sense from nonsense.
The edited problem is THIS:
+-----------------------------------------------------------------+
| A certain number is subtracted 4 times from twice the square |
| of the number and the result is 70. Find the number. |
+-----------------------------------------------------------------+
Solution
Let n be the (or "a") number under the problem's question.
Then, according to the condition, we have this equation
2n^2 - 4n = 70,
n^2 - 2n - 35 = 0,
(n-7)*(n+5) = 0.
So, there are two roots and two possible answers: the number is either -5 or 7.
Solved.
Question 1208021: On dart board, a player can only score 2, 6 or 9 points for a throw. What is the smallest number of throws needed to get a total score of exactly 82 points?
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
x = number of 2 pointers
y = number of 6 pointers
z = number of 9 pointers
Each variable is some nonnegative whole number {0,1,2,3,...}
2x+6y+9z = total number of points
2x+6y+9z = 82
x+y+z = number of throws
The goal is to minimize x+y+z
Since z is attached to the largest coefficient, we'll make z as large as possible to find the minimum of x+y+z.
If we made x as large as possible, then we'd be at the other end of the spectrum.
82/9 = 9.111 approximately
This rounds down to 9.
If z = 9, then 9z = 9*9 = 81
That leaves 82-81 = 1 point left, but of course there's no way to score 1 point with 2 pointers and/or 6 pointers.
So there's no way to get exactly 82 points with z = 9.
We'll decrease z by 1.
If z = 8, then 9z = 9*8 = 72
There would be 82-72 = 10 points left, and now it appears to be possible to achieve a score of 10 with 2 pointers and/or 6 pointers.
The subproblem is now 2x+6y = 10
This turns into x+3y = 5 after dividing everything by 2.
Use a bit of trial-and-error, or you can use the Extended Euclidean Algorithm, to find one solution is (x,y) = (2,1)
Sure enough 2x+6y = 2*2+6*1 = 4+6 = 10
What are some other integer solutions on x+3y = 5?
Solve for y to get y = (-1/3)x+5/3.
It has slope -1/3 which means to go from one point to another we move down 1 and right 3.
Starting at (2,1) follow the "down 1, right 3" movement pattern to arrive at (5,0)
Go back to (2,1). Follow the reverse of that movement pattern to go up 1, left 3, and you'll arrive at (-1,2)
However, recall that x cannot be negative.
The only practical nonnegative integer solutions to x+3y = 5 are (2,1) and (5,0)
In the first case we have x+y+z = 2+1+8 = 11 shots
In the second case we have x+y+z = 5+0+8 = 13 shots
The first case is the winner in terms of fewest number of throws.
Answer: 11
Answer by ikleyn(52878)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The idea of solution is to use "9 points" throws as many times as possible
in order for to gain the rest scores using "2 points" and "6 points" throws.
As soon as you get this idea, you will find the answer in one minute (or faster):
eight "9 points" throws (that will give you 72 scores), and
one "6 points" and two "2 points" throws (to get the rest 10 scores).
In all, you need 8 + 1 + 2 = 11 throws. ANSWER
-------------------
Solved.
//////////////////
In the United States, most public school students learn multiplication table in second or third grade.
(This info is from the Internet).
This problem is good to give it to the students of the 2nd or 3rd grade,
immediately after they learned the multiplication table.
It is a right way to develop their minds in a timely manner.
Question 1207757: a. A trapezium PQRS is such that PQ//RS and the perpendicular from P to RS is
40cm. If |𝑃𝑄| = 20𝑐𝑚, |𝑆𝑃| = 50𝑐𝑚 and |𝑆𝑅| = 60𝑐𝑚, calculate, correct to 2
significant figures, the
i. area of the trapezium
ii. angle QRS
Answer by Alan3354(69443)   (Show Source): (Show Source):
Question 1207257: How many integers satisfy |x+1|<4
Found 2 solutions by MathTherapy, Edwin McCravy:
Answer by MathTherapy(10556)   (Show Source): (Show Source):
You can put this solution on YOUR website!
How many integers satisfy |x+1|<4
|x + 1| < 4 denotes: x + 1 < 4 or x + 1 > - 4
When combined, we get: - 4 < x + 1 < 4
- 4 - 1 < x + 1 - 1 < 4 - 1 ----- Subtracting 1
- 5 < x < 3
The number of INTEGERS from - 5 to 3, INCLUSIVE, is: 3 - - 5 + 1 = 3 + 5 + 1 = 9. However,
these 9 INTEGERS include the 2 endpoints, - 5 and 3, which should be EXCLUDED. Therefore,
number of INTEGERS between - 5 and 3, that satisfies |x + 1| < 4 is: 9 - 2 = 7.
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
You can put this solution on YOUR website!
|x + 1| < 4
|x + 1| = 0, 1, 2, 3
x + 1 = -3,-2,-1, 0, 1, 2, 3
So exactly 7 integers will satisfy the given inequality.
They are:
x = -4,-3,-2,-1, 0, 1, 2
Edwin
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085, 5086..5130, 5131..5175, 5176..5220, 5221..5265, 5266..5310, 5311..5355, 5356..5400, 5401..5445, 5446..5490, 5491..5535, 5536..5580, 5581..5625, 5626..5670, 5671..5715, 5716..5760, 5761..5805, 5806..5850, 5851..5895, 5896..5940, 5941..5985, 5986..6030, 6031..6075, 6076..6120, 6121..6165, 6166..6210, 6211..6255, 6256..6300, 6301..6345, 6346..6390, 6391..6435, 6436..6480, 6481..6525, 6526..6570, 6571..6615, 6616..6660, 6661..6705, 6706..6750, 6751..6795, 6796..6840, 6841..6885, 6886..6930, 6931..6975, 6976..7020, 7021..7065, 7066..7110, 7111..7155, 7156..7200, 7201..7245, 7246..7290, 7291..7335, 7336..7380, 7381..7425, 7426..7470, 7471..7515, 7516..7560, 7561..7605, 7606..7650, 7651..7695, 7696..7740, 7741..7785, 7786..7830, 7831..7875, 7876..7920, 7921..7965, 7966..8010, 8011..8055, 8056..8100, 8101..8145, 8146..8190, 8191..8235, 8236..8280, 8281..8325, 8326..8370, 8371..8415, 8416..8460, 8461..8505, 8506..8550, 8551..8595, 8596..8640, 8641..8685, 8686..8730, 8731..8775, 8776..8820, 8821..8865, 8866..8910, 8911..8955, 8956..9000, 9001..9045, 9046..9090, 9091..9135, 9136..9180, 9181..9225, 9226..9270, 9271..9315, 9316..9360, 9361..9405, 9406..9450, 9451..9495, 9496..9540, 9541..9585, 9586..9630, 9631..9675, 9676..9720, 9721..9765, 9766..9810, 9811..9855, 9856..9900, 9901..9945, 9946..9990, 9991..10035, 10036..10080, 10081..10125, 10126..10170, 10171..10215, 10216..10260, 10261..10305, 10306..10350, 10351..10395, 10396..10440, 10441..10485, 10486..10530, 10531..10575, 10576..10620, 10621..10665, 10666..10710, 10711..10755, 10756..10800, 10801..10845, 10846..10890, 10891..10935, 10936..10980, 10981..11025, 11026..11070, 11071..11115, 11116..11160, 11161..11205, 11206..11250, 11251..11295, 11296..11340, 11341..11385, 11386..11430, 11431..11475, 11476..11520, 11521..11565, 11566..11610, 11611..11655, 11656..11700, 11701..11745, 11746..11790, 11791..11835, 11836..11880, 11881..11925, 11926..11970, 11971..12015, 12016..12060, 12061..12105, 12106..12150, 12151..12195, 12196..12240, 12241..12285, 12286..12330, 12331..12375, 12376..12420, 12421..12465, 12466..12510, 12511..12555, 12556..12600, 12601..12645, 12646..12690, 12691..12735, 12736..12780, 12781..12825, 12826..12870, 12871..12915, 12916..12960, 12961..13005, 13006..13050, 13051..13095, 13096..13140, 13141..13185, 13186..13230, 13231..13275, 13276..13320, 13321..13365, 13366..13410, 13411..13455, 13456..13500, 13501..13545, 13546..13590, 13591..13635, 13636..13680, 13681..13725, 13726..13770, 13771..13815, 13816..13860, 13861..13905, 13906..13950, 13951..13995, 13996..14040, 14041..14085, 14086..14130, 14131..14175, 14176..14220, 14221..14265, 14266..14310, 14311..14355, 14356..14400, 14401..14445, 14446..14490, 14491..14535, 14536..14580, 14581..14625, 14626..14670, 14671..14715, 14716..14760, 14761..14805, 14806..14850, 14851..14895, 14896..14940, 14941..14985, 14986..15030, 15031..15075, 15076..15120, 15121..15165, 15166..15210, 15211..15255, 15256..15300, 15301..15345, 15346..15390, 15391..15435, 15436..15480, 15481..15525, 15526..15570, 15571..15615, 15616..15660, 15661..15705, 15706..15750, 15751..15795, 15796..15840, 15841..15885, 15886..15930, 15931..15975, 15976..16020, 16021..16065, 16066..16110, 16111..16155, 16156..16200, 16201..16245, 16246..16290, 16291..16335, 16336..16380, 16381..16425, 16426..16470, 16471..16515, 16516..16560, 16561..16605, 16606..16650, 16651..16695, 16696..16740, 16741..16785, 16786..16830, 16831..16875, 16876..16920, 16921..16965, 16966..17010, 17011..17055, 17056..17100, 17101..17145, 17146..17190, 17191..17235, 17236..17280, 17281..17325, 17326..17370, 17371..17415, 17416..17460, 17461..17505, 17506..17550, 17551..17595, 17596..17640, 17641..17685, 17686..17730, 17731..17775, 17776..17820, 17821..17865, 17866..17910, 17911..17955, 17956..18000, 18001..18045, 18046..18090, 18091..18135, 18136..18180, 18181..18225, 18226..18270, 18271..18315, 18316..18360, 18361..18405, 18406..18450, 18451..18495, 18496..18540, 18541..18585, 18586..18630, 18631..18675, 18676..18720, 18721..18765, 18766..18810, 18811..18855, 18856..18900, 18901..18945, 18946..18990, 18991..19035, 19036..19080, 19081..19125, 19126..19170, 19171..19215, 19216..19260, 19261..19305, 19306..19350, 19351..19395, 19396..19440, 19441..19485, 19486..19530, 19531..19575, 19576..19620, 19621..19665, 19666..19710, 19711..19755
|



