Question 1208311: How many intergers between 31 and 131 are divisible by 7 but not divisible by 6?
Found 4 solutions by math_tutor2020, ikleyn, MathTherapy, greenestamps:
Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website! 31/7 = 4.4286
7*4 = 28 is too small but 7*5 = 35 fits
131/7 = 18.7143
7*18 = 126 also fits
7*19 = 133 is too large.
The multiples of 7 between 31 and 131 are: {35, 42, 49, ..., 126}
They can be written as {7*5, 7*6, 7*7, ..., 7*12, ..., 7*18}
Cross off 7*6, 7*12 and 7*18 since they involve 6 as a factor.
There are 14 items in the set {5,6,7,...,18} because 18-5+1 = 14. Or you can count out the items.
That must mean there are also 14 items in the set {7*5,7*6,...,7*18} = {35,42,...,126}
We crossed off 3 items {7*6,7*12,7*18} so we have 14-3 = 11 multiples of 7 between 31 and 131 such that 6 isn't a factor.
Answer: 11
Answer by ikleyn(52786)  (Show Source):
You can put this solution on YOUR website! .
How many integers between 31 and 131 are divisible by 7 but not divisible by 6?
~~~~~~~~~~~~~~~~~~~~~~
In the interval between 31 and 131, first integer number divisible by 7 is 35,
and they go with the step of 7 to the last integer divisible by 7, which is 126.
From 35 to 126, there are 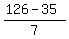 +  = 14 integer numbers divisible by 7.
From this number 14, we should subtract the number of those integers
that are divisible by both 6 and 7 simultaneously.
These integers are divisible by 42, too, and their number is 3,
because there are 3 (three) such integer numbers
42, 84 and 126.
So, we subtract 3 from 14, and we get the
ANSWER. Between 31 and 131, there are 14-3 = 11 integers that are divisible by 7 but not divisible by 6.
Solved.
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website!
How many intergers between 31 and 131 are divisible by 7 but not divisible by 6?
We start with 
Since 28 is SMALLER than 31, we ADD 7 to 28 to get 28 + 7 = 35, the SMALLEST INTEGER
between 31 and 131, that is DIVISIBLE by/is a MULTIPLE of 7.
We then continue with 
Since 126 is SMALLER than 131, we get 126 as the LARGEST INTEGER between 31 and 131, that is
DIVISIBLE by/is a MULTIPLE of 7.
So, ALL INTEGERS between 31 and 131, that are DIVISIBLE by/are MULTIPLES of 7, begin at 35 and end at 126.
So, the TOTAL number of INTEGERS, between 31 and 131, that are DIVISIBLE by/are
MULTIPLES of 7, is 
INTEGERS between 31 and 131, that are DIVISIBLE by both 7 and 6, start at 7(6) = 42.
We then continue with 
Since 126 is SMALLER than 131, we get 126 as the LARGEST INTEGER between 31 and 131, that is
DIVISIBLE by/is a MULTIPLE of 42.
So, the TOTAL number of INTEGERS between 31 and 131, that are DIVISIBLE by/are
MULTIPLES of 7 and 6, or 42, is 
TOTAL number of INTEGERS between 31 and 131, that are DIVISIBLE by/are MULTIPLES
of 7, but are NOT DIVISIBLE by/are NOT MULTIPLES of 6 (or 42) = 14 - 3 = 11
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
The range is 100, from 31 to 131; and neither 31 nor 131 is divisible by 7. So the number of integers divisible by 7 in the given range is 100/7 = 14 (and a fraction that we don't care about).
The numbers in the given range that are divisible by both 7 and 6 are the multiples of 7*6 = 42. In the given range, there are 3 such numbers: 42, 84, and 126.
So the number of integers in the given range that are divisible by 7 but not by 6 is 14-3 = 11.
ANSWER: 11
|
|
|
