Question 1132291: How many pairs of positive integers m,n satisfy 1/m + 4/n=1/12, where m is an odd integer less than 60?
Found 2 solutions by MathLover1, greenestamps:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! We are given that  such that such that  is odd and is odd and  . .
Let us try and find out the value of  in terms of in terms of 
=> 
=> 
=>
=>
=>
So, we can say that 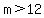
Possible odd values of such that such that 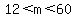 are are
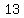 | |  | |  | |  | |  | | 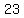 | | 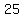 | | | |  | | 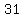 | | | | | | | | | | | |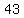 | | | | | |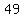 | | | | | | | |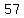 | |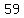 | ( | ( integers) integers)
check possible pairs:
 , , 
 , , 
 , , (irreducible)=> not an integer (irreducible)=> not an integer
same is if  =>irreducible =>irreducible
 , , 
 , , =>irreducible =>irreducible
 , ,  (irreducible) (irreducible)
 , ,  (irreducible) (irreducible)
 , , (irreducible) (irreducible)
 , ,  (irreducible) (irreducible)
 , ,  (irreducible) (irreducible)
 , ,  (irreducible) (irreducible)
and rest are irreducible
so, you have 3 pairs that satisfy given condition
 , , => => , ,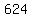
 , , => => , ,
 , ,  => => , ,
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Tutor @MathLover1 has the right answers.
Here is a way to find them without trying all the odd integers less than 60.
In her solution, she shows algebraically that

Perform the division indicated by that expression:

In this form, 48 is an integer, and n has to be an integer; that means 576/(m-12) has to be an integer.
The problem requires m to be an odd integer; that means m-12 is an odd integer.
The prime factorization of 576 is (2^6)(3^2).
Therefore, for 576/(m-12) to be an integer, with m-12 odd, m-12 has to be a factor of 3^2.
So the only possible values of m-12 are 1, 3, and 9; that makes the possible values of m 13, 15, and 21.
m = 13 --> n = 48+576/1 = 48+576 = 624
m = 15 --> n = 48+576/3 = 48+192 = 240
m = 21 --> n = 48+576/9 = 48+64 = 112
|
|
|