|
Question 258806: A charter bus company has determined that the cost of providing x people a tour is
C(x) = 180.00 + 2.50 x.
A full tour is 60 people. The cost of a ticket is $15.00 plus $0.25 for each unsold ticket. Determine (a) the revenue function, (b) the profit function, (c) the company’s maximum profit, and (d) the number of ticket sales that yields the maximum profit.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A charter bus company has determined that the cost of providing x people a tour is
C(x) = 180.00 + 2.50x.
A full tour is 60 people. The cost of a ticket is $15.00 plus $0.25 for each unsold ticket.
Determine
(a) the revenue function,
r = x(.25(60-x)+15)
r = x(15 -.25x + 15)
r = x(30-.25x)
r = -.25x^2 + 30x
:
(b) the profit function,
p = r - c
p = -.25x^2 + 30x - (180+2.5x)
p = -.25x^2 + 30x - 180 - 2.5x
p = -.25x^2 + 27.5x - 180
:
(c) the company’s maximum profit,
Find the axis of symmetry on the above equation, x = -b/(2a); a=-.25, b=27.5
x = 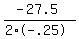
x = 55 passengers for max profit
Find actual profit, replace x with 55
p = -.25(55^2) + 27.5(55) - 180
p = -.25(3025) + 1512.5 - 180
p = -756.25 + 1512.5 - 180
p = $576.25 profit at 55 passengers
:
(d) the number of ticket sales that yields the maximum profit.
We did that when we determined the profit; x = 55 passengers
:
It may be interesting to see this graphically

where
x = no. of passengers
y = $$
Profit is green, revenue is purple. the difference between them represents the cost
:
Note that graph is not valid past x=60
|
|
|
| |