Question 662795: An average score of 80 to 90 in a math class receives a B grade. A student has scores of 92, 66, 72 and 88 of four tests. Find the range of scores on the fifth test that will give the student a B for the course.
Found 2 solutions by lynnlo, KMST:
Answer by lynnlo(4176)   (Show Source):
Answer by KMST(5328)  (Show Source):
You can put this solution on YOUR website! I interpret the wording as meaning that 80 and 90 are both a B.
I'll solve based on that.
WITH ROUNDING:
If we are going to be realistic, we have to consider rounding.
I expect that an average of 79.5 would be rounded up to 80, and would be enough for a B.
I expect that an average of 90.5 would be rounded up to 91, and that would be enough for an A,
but any average of less than 90.5 (even a 90.4) would be a B.
So I am starting from
I am assuming they calculate the average as the sum of all tests grades divided by the number of tests.
If the score in the last test is  , the average will be
Now my equation is
Multiplying all sides of the signs times 5, we get an equivalent inequality
 --> 
Subtracting 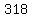 from all sides of the signs, we an the equivalent inequality
-->  --> 
So there is no possibility of getting an A, and a score of  in the fifth test is needed to get an A as the final grade.
WITH ROUNDING:
If the average has to be exactly 80.0 for a B,
then  -->  -->  , and an  in the fifth test is needed for a B.
|
|
|
