Question 484159: How many 3 1/3' feet pieces of wire can you cut from a 68' foot long
Found 4 solutions by jorel1380, Theo, ikleyn, greenestamps:
Answer by jorel1380(3719)   (Show Source): (Show Source):
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! you need to divide 68 by (3 and 1/3)
3 and 1/3 is equivalent to 10/3
you need to divide 68 by 10/3.
this is equivalent to multiplying 68 by 3/10.
your answer becomes (68*3)/10 which is equal to 204/10 which is equal to 20.4
the integer portion of 20.4 is the number of (3 and 1/3) feet pieces of wire you can cut from the 68 foot long wire.
the fractional portion is what's left over.
the integer part comes out to be a total of 20 * (3 and 1/3) = (60 + 20/3) which is equal to (66 + 2/3) feet.
the fractional part comes out to be a total of .4 * (3 and 1/3) = 4/10 * (3 and 1/3) = (4/10 * 3) + (4/10 * 1/3) = (12/10 + 4/30)
you have the 20 * (3 and 1/3) feet length that come up to a total of (66 and 2/3 feet).
you have the .4 * (3 and 1/3) feet length that comes up to a total of (12/10 + 4/30 feet). this is equivalent to (36/30 + 4/30) = 40/30 = 4/3 = (1 and 1/3).
add (66 and 2/3) to (1 and 1/3) and you get (67 and 3/3) which comes up to be 68.
the calculations are correct.
your answer is that you can get 20 pieces of (3 and 1/3) foot lengths of wire from the 68 foot length wire with one remaining length of (1 and 1/3) feet.
Answer by ikleyn(52866)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
How many 3 1/3' feet pieces of wire can you cut from a 68' foot long
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
3  = =  = =  . .
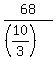 = = 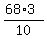 - - 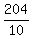 = 20 = 20  = 20 = 20  .
So, you may have 20 whole pieces of the required length and the 21-th piece of the shorter length.
ANSWER. You can cut 20 pieces of the length 3 1/3' long. .
So, you may have 20 whole pieces of the required length and the 21-th piece of the shorter length.
ANSWER. You can cut 20 pieces of the length 3 1/3' long.
Solved.
This is all what you need to do. This is all your teacher wants from you.
---------------------------------
This problem is specially created for beginner students to teach them to work freely
with improper fractions and to convert freely mixed fractions to improper fractions.
So, the way as I solved the problem for you, is the way how this problem is designed to teach you,
in precise accordance with your school curriculum.
If you will avoid manipulating with fractions, you will never master this technique
and always will fill yourself as a person who missed something important in your school mathematical education.
So, absorb everything from my post - - - use every opportunity.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
As this problem is posed, worded and presented in the post, it is clear
that this request is to provide a standard method/methodology/solution
in the frame of a typical school curriculum for a beginner student,
who first time touches fractions and makes his/her first steps.
Therefore, if the visitor is not a person of caliber Archimedes/Galileo/Newton/Euler/Einstein,
(which is, obviously, not a case), the first way for him is to learn a technique as presented in my post,
without being distracted. Any sidestep for such a visitor is a road to nowhere.
Once the standard methodology is mastered, this student can expand their knowledge in any other way
they find most suitable - for example, solving by the way as proposed by the tutor @greenestamps.
As I see from the posts of other tutors, related to this problem, I am not alone in this my position.
Other tutors provided similar solutions to mine, sharing my point that this kind of technique must be studied first,
because it establishes a basis.
Some people propose to build a house starting from the roof,
but I prefer to build it starting from the ground.
A house of knowledge in the mind of students - it is what I mean.
Answer by greenestamps(13206)   (Show Source): (Show Source):
You can put this solution on YOUR website!
You can solve this mentally, without having to deal with dividing by improper fractions, by seeing that 3 1/3 feet is exactly one-third of 10 feet.
So you can get 3 pieces of length 3 1/3 feet from each 10 feet of wire, which means 3*6 = 18 pieces from 10*6 = 60 feet of wire. Then from the remaining 8 feet of wire you can get another 2 pieces of length 3 1/3 feet, for a total of 18+2 = 20 pieces.
ANSwER: 20
|
|
|