Question 1170726: A player throws a ball straight up toward the roof of a gym. The height hin feet of the ball after tseconds can be modeled by the function h(t)=-16t^2+55t+4
a. The height of the gym roof is 53 feet. Will the ball hit the ceiling?
b. How long will it take for the ball to reach a height of 29 feet?
c. How high will the ball be 3 seconds after it’s thrown?
d. How high will be ball be 6.5 seconds after it’s thrown?
e. What is the maximum height the ball will reach?
f. How long will it take to reach that height?
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A player throws a ball straight up toward the roof of a gym. The height hin feet of the ball after t seconds
can be modeled by the function h(t)=-16t^2+55t+4
a. The height of the gym roof is 53 feet. Will the ball hit the ceiling?
b. How long will it take for the ball to reach a height of 29 feet?
c. How high will the ball be 3 seconds after it’s thrown?
d. How high will be ball be 6.5 seconds after it’s thrown?
e. What is the maximum height the ball will reach?
f. How long will it take to reach that height?
~~~~~~~~~~~~
I will place the questions and the answers in other, more natural order f), e), a), b), c) and d).
f. How long will it take to reach the maximum height?
It is about finding the maximum of the quadratic function
h(t) = -16t^2 + 55t + 4. (1)
Use the formula 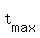 = =  , where "a" is the coefficient at the quadratic term
and "b" is the coefficient at the linear term.
e. What is the maximum height the ball will reach?
Substitute the value of , where "a" is the coefficient at the quadratic term
and "b" is the coefficient at the linear term.
e. What is the maximum height the ball will reach?
Substitute the value of 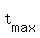 , found in part f), into the formula (1).
In this way, you will find the value of , found in part f), into the formula (1).
In this way, you will find the value of  .
a. The height of the gym roof is 53 feet. Will the ball hit the ceiling?
Compare the value of .
a. The height of the gym roof is 53 feet. Will the ball hit the ceiling?
Compare the value of  , found in part e) above with the height of the celling of 53 ft.
b. How long will it take for the ball to reach a height of 29 feet?
To answer this question, solve the equation -16t^2 + 55t + 4 = 29.
c. How high will the ball be 3 seconds after it’s thrown?
To answer this question, substitute the value of t= 3 seconds into the formula (1).
d. How high will be ball be 6.5 seconds after it’s thrown?
To answer this question, substitute the value of t= 6.5 seconds into the formula (1)
If the result is greater than zero, then it is real height.
If the result is negative, then the answer is h(t) = 0, which means "the ball just reached the floor". , found in part e) above with the height of the celling of 53 ft.
b. How long will it take for the ball to reach a height of 29 feet?
To answer this question, solve the equation -16t^2 + 55t + 4 = 29.
c. How high will the ball be 3 seconds after it’s thrown?
To answer this question, substitute the value of t= 3 seconds into the formula (1).
d. How high will be ball be 6.5 seconds after it’s thrown?
To answer this question, substitute the value of t= 6.5 seconds into the formula (1)
If the result is greater than zero, then it is real height.
If the result is negative, then the answer is h(t) = 0, which means "the ball just reached the floor".
You are fully instructed now.
If you want to see other similar problems solved, look into the lessons
- Problem on an arrow shot vertically upward
- Problem on a ball thrown vertically up from the top of a tower
Consider these lessons as your textbook, handbook, tutorials, TEMPLATES, and/or (free of charge) home teacher.
Read them attentively and learn how to solve this type of problems once and for all.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the topic "Projectiles launched/thrown and moving vertically up and dawn".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
|
|
|