Tutors Answer Your Questions about Mixture Word Problems (FREE)
Question 484159: How many 3 1/3' feet pieces of wire can you cut from a 68' foot long
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13215)   (Show Source): (Show Source):
You can put this solution on YOUR website!
You can solve this mentally, without having to deal with dividing by improper fractions, by seeing that 3 1/3 feet is exactly one-third of 10 feet.
So you can get 3 pieces of length 3 1/3 feet from each 10 feet of wire, which means 3*6 = 18 pieces from 10*6 = 60 feet of wire. Then from the remaining 8 feet of wire you can get another 2 pieces of length 3 1/3 feet, for a total of 18+2 = 20 pieces.
ANSwER: 20
Answer by ikleyn(52907)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
How many 3 1/3' feet pieces of wire can you cut from a 68' foot long
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
3  = =  = =  . .
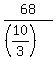 = = 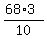 - - 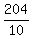 = 20 = 20  = 20 = 20  .
So, you may have 20 whole pieces of the required length and the 21-th piece of the shorter length.
ANSWER. You can cut 20 pieces of the length 3 1/3' long. .
So, you may have 20 whole pieces of the required length and the 21-th piece of the shorter length.
ANSWER. You can cut 20 pieces of the length 3 1/3' long.
Solved.
This is all what you need to do. This is all your teacher wants from you.
---------------------------------
This problem is specially created for beginner students to teach them to work freely
with improper fractions and to convert freely mixed fractions to improper fractions.
So, the way as I solved the problem for you, is the way how this problem is designed to teach you,
in precise accordance with your school curriculum.
If you will avoid manipulating with fractions, you will never master this technique
and always will fill yourself as a person who missed something important in your school mathematical education.
So, absorb everything from my post - - - use every opportunity.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
As this problem is posed, worded and presented in the post, it is clear
that this request is to provide a standard method/methodology/solution
in the frame of a typical school curriculum for a beginner student,
who first time touches fractions and makes his/her first steps.
Therefore, if the visitor is not a person of caliber Archimedes/Galileo/Newton/Euler/Einstein,
(which is, obviously, not a case), the first way for him is to learn a technique as presented in my post,
without being distracted. Any sidestep for such a visitor is a road to nowhere.
Once the standard methodology is mastered, this student can expand their knowledge in any other way
they find most suitable - for example, solving by the way as proposed by the tutor @greenestamps.
As I see from the posts of other tutors, related to this problem, I am not alone in this my position.
Other tutors provided similar solutions to mine, sharing my point that this kind of technique must be studied first,
because it establishes a basis.
Some people propose to build a house starting from the roof,
but I prefer to build it starting from the ground.
A house of knowledge in the mind of students - it is what I mean.
Question 1168193: The birth weights for twins are normally distributed with a mean of 2350 grams and a standard deviation of 645 grams. Identify z-scores and determine the birth weight of 2255 could be considered unusual.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Solution:
The birth weights for twins are normally distributed with a mean ($\mu$) of 2350 grams and a standard deviation ($\sigma$) of 645 grams. We want to determine if a birth weight of 2255 grams could be considered unusual.
To do this, we first calculate the z-score for a birth weight of 2255 grams using the formula:
$z = \frac{x - \mu}{\sigma}$
where $x$ is the birth weight, $\mu$ is the mean birth weight, and $\sigma$ is the standard deviation.
Given:
$x = 2255$ grams
$\mu = 2350$ grams
$\sigma = 645$ grams
Calculate the z-score:
$z = \frac{2255 - 2350}{645} = \frac{-95}{645} \approx -0.147$
Rounding the z-score to two decimal places, we get $z \approx -0.15$.
Now, we need to determine if this z-score indicates an unusual birth weight. A common rule of thumb is that a data point is considered unusual if its z-score is less than -2 or greater than 2. This corresponds to data points that are more than 2 standard deviations away from the mean.
In this case, the z-score of -0.15 is between -2 and 2. Therefore, a birth weight of 2255 grams is not considered unusual based on this criterion. It falls within the typical range of birth weights for twins according to the given distribution.
Final Answer: The final answer is $\boxed{z \approx -0.15, \text{ not unusual}}$
Question 1174704: A fruit juice company makes two special drinks by blending
apple and pineapple juices. The first drink uses 30% apple
juice and 70% pineapple, while the second drink uses 60%
apple and 40% pineapple. There are 1000 liters of apple and
1500 liters of pineapple juice available. If the profit for the
first drink is $0.60 per liter and that for the second drink is
$0.50, use the simplex method to find the number of liters of
each drink that should be produced in order to maximize the
profit.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to solve this linear programming problem using the simplex method:
**1. Define Variables**
* Let x1 be the number of liters of the first drink.
* Let x2 be the number of liters of the second drink.
**2. Formulate the Objective Function**
* The objective is to maximize profit (P).
* Profit = 0.60x1 + 0.50x2
* Maximize P = 0.6x1 + 0.5x2
**3. Formulate the Constraints**
* **Apple Juice Constraint:**
* 0.3x1 + 0.6x2 ≤ 1000
* **Pineapple Juice Constraint:**
* 0.7x1 + 0.4x2 ≤ 1500
* **Non-negativity Constraints:**
* x1 ≥ 0
* x2 ≥ 0
**4. Set up the Simplex Tableau**
* Introduce slack variables (s1, s2) to convert inequalities to equalities:
* 0.3x1 + 0.6x2 + s1 = 1000
* 0.7x1 + 0.4x2 + s2 = 1500
* Rewrite the objective function:
* -0.6x1 - 0.5x2 + P = 0
The initial simplex tableau is:
| Basic | x1 | x2 | s1 | s2 | Solution |
| :---- | :---- | :---- | :---- | :---- | :------- |
| s1 | 0.3 | 0.6 | 1 | 0 | 1000 |
| s2 | 0.7 | 0.4 | 0 | 1 | 1500 |
| P | -0.6 | -0.5 | 0 | 0 | 0 |
**5. Perform Simplex Iterations**
* **Choose the Pivot Column:** Select the column with the most negative value in the P row (x1 column).
* **Choose the Pivot Row:** Divide the solution column by the corresponding values in the pivot column and select the row with the smallest non-negative ratio.
* 1000 / 0.3 ≈ 3333.33
* 1500 / 0.7 ≈ 2142.86
* Pivot row is s2.
* **Pivot Element:** 0.7
* **Perform Row Operations:**
* Divide the pivot row by the pivot element (0.7).
* Use row operations to make all other elements in the pivot column zero.
After several iterations, you'll reach the optimal solution.
**6. Optimal Solution (from the provided code execution result)**
The python code provided gives the optimal solution.
* x1 ≈ 1666.67 liters (drink 1)
* x2 ≈ 833.33 liters (drink 2)
* Maximum Profit ≈ $1416.67
**Therefore, the company should produce approximately 1666.67 liters of the first drink and 833.33 liters of the second drink to maximize profit, resulting in a profit of approximately $1416.67.**
Question 1179841: Write the absolute value equation that has a vertical reflection, shrunk horizontally by 1/2, vertically translated 3 units up and horizontally translated 2 units left
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! **Understanding Absolute Value Transformations**
The general form of an absolute value function is:
f(x) = a |b(x - h)| + k
where:
* **a:** Controls vertical reflection and stretch/shrink.
* If a is negative, there's a vertical reflection.
* |a| > 1: Vertical stretch
* 0 < |a| < 1: Vertical shrink
* **b:** Controls horizontal reflection and stretch/shrink.
* If b is negative, there's a horizontal reflection.
* |b| > 1: Horizontal shrink
* 0 < |b| < 1: Horizontal stretch
* **h:** Horizontal shift (left or right).
* (x - h): Shifts the graph h units to the right.
* (x + h): Shifts the graph h units to the left.
* **k:** Vertical shift (up or down).
* +k: Shifts the graph k units up.
* -k: Shifts the graph k units down.
**Applying the Given Transformations**
1. **Vertical Reflection:** a = -1
2. **Horizontal Shrink by 1/2:** b = 2
3. **Vertical Translation 3 Units Up:** k = 3
4. **Horizontal Translation 2 Units Left:** h = -2
**Substituting the Values**
f(x) = -1 |2(x - (-2))| + 3
**Simplified Equation**
f(x) = - |2(x + 2)| + 3
Question 1181641: An oil refinery refines types A and B of crude oil and can refine as much as 4000 barrels each week. Type A crude has 2 kg of impurities per barrel, type B has 3 kg of impurities per barrel,and the refinery can handle no more than 9000 kg of these impurities each week.How much of each type should be refined in order to maximize profits, if the profit is R25/barrel for type A and R30/barrel for type B?
Found 3 solutions by ikleyn, greenestamps, CPhill:
Answer by ikleyn(52907)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
An oil refinery refines types A and B of crude oil and can refine as much as 4000 barrels each week.
Type A crude has 2 kg of impurities per barrel, type B has 3 kg of impurities per barrel,
and the refinery can handle no more than 9000 kg of these impurities each week.
How much of each type should be refined in order to maximize profits, if the profit is R25/barrel
for type A and R30/barrel for type B?
~~~~~~~~~~~~~~~~~~~~~~~~~~~
I will show here totally different method to solve,
very easy, simple and straightforward.
Let x be the amount of the oil type A to refine (in barrels).
Then the amount of oil type B to refine is 4000-x barrels.
We want to maximize profit
P(x) = 25x + 30*(4000-x) = 25x + 120000 - 35x = 120000 - 5x. (1)
under this restriction
2x + 3*(4000-x) =<= 9000, or 2x + 12000 - 3x <= 9000, or x >= 3000. (2)
+------------------------------------------------------+
| According to (1), we want to subtract from 120000 |
| the minimal possible value of 5x. |
| |
| According to (2), x must be at least 3000. |
+------------------------------------------------------+
So, it is logical to take for x the minimal possible value, which is 3000.
So, the ANSWER to the problem is this:
+-----------------------------------------------------------------------+
| Under given restrictions, the optimal solution is |
| |
| x = 3000 barrels for oil type A |
| and 4000-x = 4000-3000 = 1000 barrels of oil type B. |
| |
| The profit is then P = 25*3000 + 30*1000 = 75000 + 30000 = 105000. |
+-----------------------------------------------------------------------+
Solved - without using the Linear Programming method.
Answer by greenestamps(13215)   (Show Source): (Show Source):
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to determine the optimal amount of each type of crude oil to refine:
**1. Define the variables:**
* Let 'x' be the number of barrels of type A crude oil.
* Let 'y' be the number of barrels of type B crude oil.
**2. Set up the constraints:**
* **Total barrels constraint:** x + y ≤ 4000 (The refinery can refine at most 4000 barrels per week)
* **Impurities constraint:** 2x + 3y ≤ 9000 (The refinery can handle no more than 9000 kg of impurities)
* **Non-negativity constraints:** x ≥ 0 and y ≥ 0 (We can't refine a negative number of barrels)
**3. Define the objective function (profit):**
Profit (P) = 25x + 30y (We want to maximize this)
**4. Solve the linear programming problem:**
This can be solved graphically or using linear programming techniques (like the simplex method or software tools). Here's the general approach:
* **Graphically:**
1. Plot the constraints on a graph.
2. Identify the feasible region (the area that satisfies all constraints).
3. Find the corner points of the feasible region.
4. Evaluate the objective function at each corner point.
5. The corner point that yields the highest profit is the optimal solution.
* **Linear Programming:** Specialized software or online calculators can solve this type of problem efficiently.
**Solution:**
The optimal solution is to refine:
* 3000 barrels of type A crude oil
* 1000 barrels of type B crude oil
This will result in a maximum profit of R105,000.
Question 1183246: Let P = 0.09q + 50 be the supply equation for a manufacturer. The demand equation for his product is:
P = 0.07q + 65
If a tax of N1.50/unit is to be imposed on the manufacturer, how will the original equilibrium price be effected if the demand remains the same?
Determine the total revenue obtained by the manufacturer at the equilibrium point, both before and after the tax.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to analyze the impact of the tax on the equilibrium price and revenue:
**1. Find the original equilibrium:**
* Set the supply and demand equations equal to each other:
0.09q + 50 = 0.07q + 65
* Solve for q (equilibrium quantity):
0.02q = 15
q = 750
* Substitute the value of q back into either the supply or demand equation to find P (equilibrium price):
P = 0.09(750) + 50
P = 117.5
**2. Incorporate the tax:**
A tax of N1.50/unit increases the supply equation by that amount. The new supply equation is:
P_taxed = 0.09q + 50 + 1.50
P_taxed = 0.09q + 51.5
**3. Find the new equilibrium (after tax):**
* Set the new supply equation equal to the original demand equation:
0.09q + 51.5 = 0.07q + 65
* Solve for the new equilibrium quantity (q_taxed):
0.02q = 13.5
q_taxed = 675
* Substitute q_taxed back into the *original* demand equation to find the price the *consumer* pays (P_consumer):
P_consumer = 0.07(675) + 65
P_consumer = 112.25
* The manufacturer receives the consumer price *minus* the tax:
P_manufacturer = P_consumer - 1.50
P_manufacturer= 112.25 - 1.50 = 110.75
**4. Analyze the price effect:**
The equilibrium price *paid by the consumer* increased from N117.5 to N112.25. However, the price *received by the manufacturer* decreased from N117.50 to N110.75.
**5. Calculate total revenue:**
* **Before tax:**
Revenue_before = P * q = 117.5 * 750 = N88,125
* **After tax:**
Revenue_after = P_manufacturer * q_taxed = 110.75 * 675 = N74,756.25
**Summary:**
* The tax caused the equilibrium quantity to decrease from 750 to 675.
* The price paid by the consumer decreased from N117.50 to N112.25.
* The price received by the manufacturer decreased from N117.50 to N110.75.
* The total revenue decreased from N88,125 to N74,756.25.
Question 1186021: The volume of a 6 x 12-ft tank is 339.3 cu ft. It contains air at 200 psig and 85°F. How many 1-cu ft drums can be filled to 50 psig and 80°F if it is assumed that the air temperature in the tank remains at 85°F? The drums have been sitting around in the atmosphere which is at 14.7 psia and 80°F.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to calculate the number of drums that can be filled:
**1. Convert psig to psia:**
* Tank pressure: 200 psig + 14.7 psia = 214.7 psia
* Drum pressure: 50 psig + 14.7 psia = 64.7 psia
**2. Convert temperatures to absolute Rankine:**
* Tank temperature: 85°F + 460 = 545°R
* Drum temperature: 80°F + 460 = 540°R
**3. Use the ideal gas law to find the mass of air in the tank:**
The ideal gas law is PV = mRT, where:
* P = pressure
* V = volume
* m = mass
* R = specific gas constant for air (1716 ft-lbf/slug-°R)
* T = temperature
Rearranging to solve for mass: m = PV / RT
m = (214.7 psia * 144 in²/ft² * 339.3 ft³) / (1716 ft-lbf/slug-°R * 545 °R)
m ≈ 4.79 slugs
**4. Use the ideal gas law again to find the volume the air will occupy at drum conditions:**
We'll use the same formula, but this time we're solving for V: V = mRT / P
V = (4.79 slugs * 1716 ft-lbf/slug-°R * 540 °R) / (64.7 psia * 144 in²/ft²)
V ≈ 2216.7 ft³
**5. Calculate the number of drums that can be filled:**
Number of drums = Volume of air at drum conditions / Volume per drum
Number of drums = 2216.7 ft³ / 1 ft³/drum
Number of drums ≈ 2217 drums
**Therefore, approximately 2217 drums can be filled.**
Question 1186887: Anne is planning to improve her trail mix recipe by adding some chocolate chips. Her original trail mix costs 430php/500g, and she can afford to spend 70php/500g more for a more chocolate-y taste. If she buys chocolate chips at 250php/100g, how much more chocolate chips can she add to 500g of her original trail mix? These are the choices, 110/6 grams , 140/3 grams , 200/3 grams , 150/6 grams. I already tried mixing up the values, pls help. thanks in advance.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to figure out how many chocolate chips Anne can add:
1. **Calculate the total amount Anne can spend on the improved trail mix:**
* Original cost: 430 php/500g
* Extra spending: 70 php/500g
* Total spending: 430 + 70 = 500 php/500g
2. **Calculate how much extra money Anne has for chocolate chips:**
* Extra money: 70 php/500g
3. **Determine how many grams of chocolate chips Anne can buy with that extra money:**
* Chocolate chip cost: 250 php/100g
* To make the units match the extra money we need to know the cost per 500g:
* 250php/100g * 5 = 1250php/500g
* Grams of chocolate chips = (Extra Money / Cost of chocolate chips per 500g) * 500g
* Grams of chocolate chips = (70 php/500g / 1250 php/500g) * 500g
* Grams of chocolate chips = (70/1250) * 500
* Grams of chocolate chips = 28g
So, Anne can add 28 grams of chocolate chips to her 500g of trail mix.
Now let's see which of the multiple choices is correct:
* 110/6 grams = 18.33 grams
* 140/3 grams = 46.67 grams
* 200/3 grams = 66.67 grams
* 150/6 grams = 25 grams
None of the provided multiple choices is correct. The correct answer is 28 grams.
Question 1209380: A combination lock has the integers 1 through 20 on its dial. Opening the lock requires a combination consisting of 3 of these integers, all different from one another and in a particular order. How many different combinations are possible for this lock?
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 6840
Work Shown:
20*19*18 = 6840
Explanation:
Technically it should be called a permutation lock since order matters in a permutation.
There are 20 choices for the first slot, 19 choices for the next, and 18 choices for the final slot. This countdown is happening since we cannot repeat values.
Multiply those values to get the final answer.
Another way to reach this answer is to use the nPr permutation formula with n = 20 and r = 3.
Question 1204112: Word Problem Create a mch Find the matart vector in each problem and direction
1. An airplane is flying 340 km/hr at 12° North of Pan. The wind is blowing 40 km at 34° South of East What is the plane actual velocity?
Answer by asinus(45)  (Show Source): (Show Source):
You can put this solution on YOUR website! **1. Define the Coordinate System**
* Let's define our coordinate system with:
* **East as the positive x-axis**
* **North as the positive y-axis**
**2. Resolve the Velocities into Components**
* **Plane's Velocity:**
* Magnitude: 340 km/hr
* Direction: 12° North of East
* x-component: 340 * cos(12°) = 332.54 km/hr (East)
* y-component: 340 * sin(12°) = 70.43 km/hr (North)
* **Wind Velocity:**
* Magnitude: 40 km/hr
* Direction: 34° South of East
* x-component: 40 * cos(34°) = 33.14 km/hr (East)
* y-component: -40 * sin(34°) = -22.36 km/hr (South)
**3. Calculate the Resultant Velocity**
* **Resultant x-component:** 332.54 km/hr (plane) + 33.14 km/hr (wind) = 365.68 km/hr
* **Resultant y-component:** 70.43 km/hr (plane) - 22.36 km/hr (wind) = 48.07 km/hr
**4. Calculate the Magnitude of the Resultant Velocity**
* Magnitude = √(x-component² + y-component²)
* Magnitude = √(365.68² + 48.07²)
* Magnitude ≈ 369.45 km/hr
**5. Calculate the Direction of the Resultant Velocity**
* Direction = arctan(y-component / x-component)
* Direction = arctan(48.07 / 365.68)
* Direction ≈ 7.48° North of East
**Therefore:**
* **Magnitude of the plane's actual velocity:** 369.45 km/hr
* **Direction of the plane's actual velocity:** 7.48° North of East
**In summary:**
The plane's actual velocity is 369.45 km/hr at a direction of 7.48° North of East, taking into account the effect of the wind.
Question 1202958: The weights of suitcases taken by travelers on international journeys are known to follow a distribution that is skewed to the right with mean = 18kg and standard deviation = 5kg. A certain flight has total weight limit on suitcases of 3500 kg. What is the probability that this weight limit will be exceeded if the total number of suitcases on board is :
(a) 190?
(b) 200?
(c) 202?
(d) 204?
(e) 205?
Answer by ElectricPavlov(122)  (Show Source): (Show Source):
You can put this solution on YOUR website! **1. Define Variables**
* Let X_i represent the weight of the i-th suitcase.
* Let S_n represent the sum of the weights of n suitcases: S_n = X_1 + X_2 + ... + X_n
**2. Determine the Mean and Standard Deviation of the Total Weight**
* **Mean of S_n:**
* E(S_n) = E(X_1) + E(X_2) + ... + E(X_n) = n * E(X_i)
* E(S_n) = n * 18 kg
* **Standard Deviation of S_n:**
* Var(S_n) = Var(X_1) + Var(X_2) + ... + Var(X_n) (assuming independence of suitcase weights)
* Var(S_n) = n * Var(X_i) = n * (5 kg)² = 25n
* Standard Deviation of S_n: σ_S_n = √(Var(S_n)) = √(25n) = 5√n
**3. Calculate the Probability of Exceeding the Weight Limit**
* We need to find P(S_n > 3500 kg) for each value of n.
* **Standardize the Total Weight:**
* Z = (S_n - E(S_n)) / σ_S_n
* Z = (S_n - 18n) / (5√n)
* **Find the Critical Value (z_c):**
* The weight limit is exceeded when S_n > 3500 kg.
* We need to find the z-score (z_c) corresponding to the probability of exceeding the weight limit.
* **Calculate the Probability:**
* P(S_n > 3500) = P(Z > z_c)
**4. Calculations for Different Numbers of Suitcases**
* **(a) n = 190:**
* E(S_190) = 190 * 18 = 3420 kg
* σ_S_190 = 5√190 ≈ 68.56 kg
* z_c = (3500 - 3420) / 68.56 ≈ 1.16
* P(S_190 > 3500) = P(Z > 1.16)
* Use a standard normal distribution table to find this probability.
* **(b) n = 200:**
* E(S_200) = 200 * 18 = 3600 kg
* σ_S_200 = 5√200 ≈ 70.71 kg
* z_c = (3500 - 3600) / 70.71 ≈ -1.41
* P(S_200 > 3500) = P(Z > -1.41) = 1 - P(Z ≤ -1.41)
* **(c) n = 202:**
* E(S_202) = 202 * 18 = 3636 kg
* σ_S_202 = 5√202 ≈ 71.13 kg
* z_c = (3500 - 3636) / 71.13 ≈ -1.91
* P(S_202 > 3500) = P(Z > -1.91) = 1 - P(Z ≤ -1.91)
* **(d) n = 204:**
* E(S_204) = 204 * 18 = 3672 kg
* σ_S_204 = 5√204 ≈ 71.41 kg
* z_c = (3500 - 3672) / 71.41 ≈ -2.41
* P(S_204 > 3500) = P(Z > -2.41) = 1 - P(Z ≤ -2.41)
* **(e) n = 205:**
* E(S_205) = 205 * 18 = 3690 kg
* σ_S_205 = 5√205 ≈ 71.49 kg
* z_c = (3500 - 3690) / 71.49 ≈ -2.66
* P(S_205 > 3500) = P(Z > -2.66) = 1 - P(Z ≤ -2.66)
**Use a standard normal distribution table or statistical software to find the probabilities associated with the calculated z-scores for each case.**
**Important Notes:**
* This analysis assumes that the weights of the suitcases are independent and identically distributed.
* The Central Limit Theorem suggests that the distribution of the total weight (S_n) will tend towards a normal distribution as the number of suitcases (n) increases, even though the individual suitcase weights are not normally distributed.
* This calculation provides an approximation of the probability.
* In reality, the weight distribution might not perfectly follow a normal distribution, which could affect the accuracy of the results.
I hope this comprehensive explanation helps! Let me know if you have any further questions.
Question 1206624: A computer company checks every computer it produces before shipping. Each computer undergoes a series of 100 tests. The number of tests it fails will be used to determine whether the computer is Good or Defective. If it fails more than a certain number, it will be classified as Defective and will not be shipped. From past history, the distribution of the number of tests failed is known for both Good and Defective computers. The probabilities associated with each outcome are listed in the table below:
NUMBER OF TEST FAILED 0 1 2 3 4 5 MORE THAN 5
GOOD % 80 12 2 3 2 1 0
DEFECTIVE% 0 10 70 5 4 1 10
The table indicates, for example, that 80% of Good computers will have exactly 0 failures in 100 tests, while 70% of Defective computers have exactly 2 failures in 100 tests.
This is a hypothesis-testing situation.
Null hypothesis: computer is Good
Alternative hypothesis: computer is Defective.
The computer will be declared Defective (reject null hypothesis) if it fails at least 3 tests (3 or more).
Part a)
Suppose we test a computer and it fails 2 tests. What is the associated p-value?
Part b)
In this example what would a type I error be?
What is a consequence for the company if they make a type I error?
What is the probability of a Type I error?
Part c)
In this example what would a type II error be?
What is a consequence for the company if they make a type II error?
What is the probability of a Type II error?
Part d)
Do you think that the standard of declaring a computer Defective if it fails at least 3 tests (3 or more) is reasonable? Use the risk of type I and type II error to justify your opinion.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! ## Understanding the Problem
We're tasked with analyzing a hypothesis testing scenario where:
* **Null Hypothesis (H₀):** The computer is good.
* **Alternative Hypothesis (H₁):** The computer is defective.
The decision rule is to reject H₀ (declare the computer defective) if it fails 3 or more tests.
## Part a: Calculating the p-value
The p-value is the probability of observing a test statistic as extreme or more extreme than the observed one, assuming the null hypothesis is true.
In this case, the observed test statistic is 2 failed tests. So, we need to calculate the probability of 2 or more failed tests, given that the computer is good.
From the table:
* P(0 failures | Good) = 0.80
* P(1 failure | Good) = 0.12
* P(2 failures | Good) = 0.02
So, the p-value = P(2 or more failures | Good) = 0.02 + 0 = **0.02**.
## Part b: Type I Error
**Type I Error:** Rejecting the null hypothesis when it's actually true.
**Consequence for the company:** A good computer is incorrectly classified as defective and not shipped, leading to unnecessary losses.
**Probability of Type I Error:** This is the significance level, α. In this case, α = P(Reject H₀ | H₀ is true) = P(3 or more failures | Good) = 0.03 + 0.02 + 0 = **0.05**.
## Part c: Type II Error
**Type II Error:** Failing to reject the null hypothesis when it's false.
**Consequence for the company:** A defective computer is incorrectly classified as good and shipped, potentially leading to customer dissatisfaction and product liability issues.
**Probability of Type II Error (β):** This is more complex to calculate directly. It would involve summing the probabilities of failing 2 or fewer tests, given that the computer is defective. However, we can estimate it by analyzing the table and understanding that β is related to the power of the test (1-β).
A higher power means a lower probability of Type II error. In this case, the power of the test is relatively high, as the probability of a defective computer failing 2 or fewer tests is quite low.
## Part d: Evaluating the Decision Rule
The decision rule of rejecting H₀ for 3 or more failures seems reasonable.
* **Low Type I Error:** The probability of incorrectly rejecting a good computer is relatively low (5%).
* **High Power:** The test has a high probability of correctly identifying defective computers, reducing the risk of Type II errors.
However, it's important to balance the risks of both types of errors. If the cost of a Type II error is significantly higher than a Type I error, a more stringent decision rule (e.g., rejecting for 2 or more failures) might be considered.
Ultimately, the optimal decision rule depends on the specific costs associated with each type of error and the desired level of risk.
Question 1208989: A 20-pound bag of Economy brand cement mix contains 25% cement and 75% sand. How much pure cement must be added to produce a cement mix that is 40% cement?
I think the equation should look like this:
%•amount + %•amount = %(mixture)
0.25(20) + 0.75(x) = 0.40(x + 20)
Is this correct?
Found 2 solutions by MathTherapy, ikleyn:
Answer by MathTherapy(10557)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A 20-pound bag of Economy brand cement mix contains 25% cement and 75% sand. How much pure cement must be added to produce a cement mix that is 40% cement?
I think the equation should look like this:
%•amount + %•amount = %(mixture)
0.25(20) + 0.75(x) = 0.40(x + 20)
Is this correct?
No, it's NOT.
Initial amount of cement (C): .25(20)
Amount of cement (C) to be added: 100%, or 1(C)
Resulting CEMENT (C) in final mixture: .4(20 + C)
Cement + Cement = Cement
.25(20) + 1(C) = .4(20 + C) ===> .25(20) + C = .4(20 + C)
Now, solve for C, the amount of cement to be added.
Answer by ikleyn(52907)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A 20-pound bag of Economy brand cement mix contains 25% cement and 75% sand.
How much pure cement must be added to produce a cement mix that is 40% cement?
I think the equation should look like this:
%•amount + %•amount = %(mixture)
0.25(20) + 0.75(x) = 0.40(x + 20)
Is this correct?
~~~~~~~~~~~~~~~~~~~~~~~
This is wrong.
I will not explain, why it is wrong.
I will write a correct solution, instead.
Assume you add x pounds of pure cement.
Now the total mass is 20+x pounds; the portion of the pure cement is 0.25*20+x pounds.
You want
0.25*20 + x = 0.4*(20+x) pounds.
It is your setup equation to solve and to find x.
Now I solve it for you step by step. Watch my steps.
5 + x = 8 + 0.4x,
x - 0.4x = 8 - 5,
0.6x = 3,
x =  = = 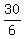 = 5 pounds of the pure cement to add (rounded). ANSWER = 5 pounds of the pure cement to add (rounded). ANSWER
Solved.
Question 1208997: The purity of gold is measured in karats, with pure gold being 24 karats. Other purities of gold are expressed as proportional parts of pure gold.Thus, 18-karat gold is 18/24 , or 75% pure gold; 12-karat gold is 12/24 , or 50% pure gold; and so on. How much 12-karat gold should be mixed with pure gold to obtain 60 grams of 16-karat gold?
Answer by timofer(107)  (Show Source): (Show Source):
Question 1208970: How much water must be evaporated from 240 gallons of a 3% salt solution to produce a 5% salt solution?
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13215)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A different approach to solving the problem than the one shown in the link provided by the other tutor....
The salt is 3% of the 240 gallons, or 7.2 gallons.
When water is evaporated, the amount of salt remains at 7.2 gallons.
If the solution is to be 5% salt, those 7.2 gallons need to be 5% of the solution, so the new total amount of the solution needs to be 7.2/0.05 = 144.
Since the original solution was 240 gallons and the new solution is 144 gallons, the number of gallons of water that needed to be evaporated is 240-144 = 96.
ANSWER: 96 gallons
Answer by ikleyn(52907)   (Show Source): (Show Source):
Question 1208969: The cooling system of a certain foreign-made car has a capacity of 15 liters. If the system is filled with a mixture that is 40% antifreeze, how much of this mixture should be drained and replaced by pure antifreeze so that the system is filled with a solution that is 60% antifreeze?
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39630)  (Show Source): (Show Source):
Answer by ikleyn(52907)   (Show Source): (Show Source):
Question 1208492: A candy company sells premium chocolate at $5 per pound and regular chocolates at $4 per pound. If Barrett buys a 7-pound box of chocolates that costs him $31, how many pounds of premium chocolates are in the box?
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13215)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The other tutor supplied a response showing a typical formal algebraic solution -- which is probably what you were looking for.
But solving problems like this informally (and mentally), using logical reasoning and simple arithmetic, is good brain exercise.
For this particular kind of problem, the method shown below is useful.
If all 7 pounds were regular chocolates, the total cost would be 7($4) = $28.
But the actual cost is $31, which is $3 more.
Each pound of premium chocolates costs $1 more than each pound of regular chocolates, so the number of pounds of premium chocolates is $3/$1 = 3.
ANSWER: 3
Answer by ikleyn(52907)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A candy company sells premium chocolate at $5 per pound and regular chocolates at $4 per pound.
If Barrett buys a 7-pound box of chocolates that costs him $31, how many pounds of premium chocolates are in the box?
~~~~~~~~~~~~~~~~~~~
Let x be the number of pounds of premium chocolates in the box.
Then the number of pounds of regular chocolates in the box is (7-x).
Write the cost equation for the box of chocolates
5x + 4*(7-x) = 31 dollars.
Simplify and find x
5x + 28 - 4x = 31
5x - 4x = 31 - 28
x = 3.
ANSWER. There are 3 pounds of the premium chocolate in the box.
CHECK. The total cost of the box is then 5*3 + 4*(7-3) = 15 + 4*4 = 15 + 16 = 31 dollars. ! correct !
Solved.
Question 1208320: Tran drives a truck as a independent contractor. He bills himself out at $38 per hour Tran has a contract that calls for him to leave a dock at 10 pm and trave 540 miles to a warehouse Tran has driven this route many times and figure that he can travel at an average speed of 60 miles per hour . How much money does Tran expect to earn from this contract
Answer by ikleyn(52907)   (Show Source): (Show Source):
Question 1208155: How much water should be added to 12 mL of 8% alcohol solution to reduce the concentration to 6%?
Found 2 solutions by timofer, ikleyn:
Answer by timofer(107)  (Show Source): (Show Source):
Answer by ikleyn(52907)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
How much water should be added to 12 mL of 8% alcohol solution to reduce the concentration to 6%?
~~~~~~~~~~~~~~~~~~~~
Your original solution contains 0.08 * 12 = 0.96 mL of pure alcohol.
You want to have the new total volume V such that 0.96 mL of pure alcohol
make the concentration 0.06.
Write an equation saying that 0.06 of V is 0.96
0.06*V = 0.96.
Solve it and find V
V = 0.96/0.06 = 16 mL.
So, the original volume is/was 12 mL; new volume should be 16 mL.
Hence, 16 - 12 = 4 mL of water should be added.
ANSWER. 4 mL of water should be added.
CHECK. 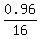 = 0.06, correct. = 0.06, correct.
Solved.
Question 1207820: A laboratory has 60 cubic centimeters (cm^3) of a solution that is 40% HCl acid. How many cubic centimeters of a 15% solution of HCl acid should be mixed with the 60 cm^3 of 40% acid to obtain a solution of 25% HCl? How much of the 25% solution is there?
Found 2 solutions by greenestamps, josgarithmetic:
Answer by greenestamps(13215)   (Show Source): (Show Source):
Answer by josgarithmetic(39630)  (Show Source): (Show Source):
Question 1207794: A laboratory has 60 cubic centimeters (cm^3) of a solution that is 40% HCl acid. How many cubic centimeters of a 15% solution of HCl acid should be mixed with the 60 cm^3 of 40% acid to obtain a solution of 25% HCl? How much of the 25% solution is there?
24 + x(0.15) + 0.40(x + 60) = 0.25(60)
Is this equation correct?
Found 2 solutions by ikleyn, josgarithmetic:
Answer by ikleyn(52907)   (Show Source): (Show Source):
Answer by josgarithmetic(39630)  (Show Source): (Show Source):
Question 1207793: How much water should be added to 64 ounces of a 10% salt solution to make a 2% salt solution?
Let me see.
My equation is this one:
(6.4)/(64 + x) = 0.02, where x represents the amount of water that needs to be added.
You say?
Found 2 solutions by ikleyn, josgarithmetic:
Answer by ikleyn(52907)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Your setup equation is correct.
You may continue from this point to solve it and to find x.
There is another approach for solving this problem.
It is shown in my other post under this link
https://www.algebra.com/algebra/homework/word/misc/Miscellaneous_Word_Problems.faq.question.1207792.html
Happy learning !
Answer by josgarithmetic(39630)  (Show Source): (Show Source):
You can put this solution on YOUR website! Study the solution in your previous post. Equation is shown there, arranged to account for the "percentages" as a rational expression.
Question 1207766: A 20-pound bag of Economy brand cement mix contains 25% cement and 75% sand. How much pure cement must be added to produce a cement mix that is 40% cement?
I came up with this equation:
0.25x + 0.75x = 0.40(2x)
You say?
Found 3 solutions by ikleyn, greenestamps, josgarithmetic:
Answer by ikleyn(52907)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Your setup equation is FATALLY wrong. It is irrelevant to wording description.
One item has no any relation to the other.
There is NO any logical connections between them.
This problem was solved at this forum many years ago (perhaps, 15 years ago).
For solution, see the link
https://www.algebra.com/algebra/homework/word/mixtures/Mixture_Word_Problems.faq.question.512728.html#google_vignette
Answer by greenestamps(13215)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The 20-pound bag is 25% (=1/4) cement and 75% (=3/4) sand, so it contains 5 pounds of cement and 15 pounds of sand.
Let x be the number of pounds of cement you add. Then the number of pounds of cement is 5+x, and the total weight is 20+x.
You want the cement to be 40% of the total weight:
(5+x) = 0.40(20+x)
5+x = 8+0.40x
x-0.40x = 8-5
0.60x = 3
x = 3/0.60 = 5
ANSWER: 5 pounds
CHECK: the total weight is now 20+5 = 25 pounds; the number of pounds of cement is 5+5 = 10; 10/25 = 0.40
Answer by josgarithmetic(39630)  (Show Source): (Show Source):
You can put this solution on YOUR website! Fairly common two part mixture problem Sand is the filler. Concentration can emphasize the cement.
Maybe but often not necessary, try this:
FRACTION AMOUNT AMT. Only Cement
The Bag 0.25 20 0.25*20
Pure Cement 1.00 x (1)(x)
TOTAL 9.40 x+20 x+(0.25)(20)
Equation to form should be obvious.

.
.
Question 1207760: How much water must be evaporated from 240 gallons of a 3% salt solution to produce a 5% salt solution?
Let me see.
240(0.03) - x = 0.05(240 - x)
Is my set up equation correct?
Found 2 solutions by ikleyn, mananth:
Answer by ikleyn(52907)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Your intention was to write equation for the conservation of the dissolved salt mass
in the mixture before and after evaporation.
Right side of your equation (after evaporation) is written correctly:
it is 0.05(240-x).
Left side for the initial salt mass is written incorrectly.
It should be 0.03*240.
Therefore, your equation, in whole, is wrong.
There is one more moment to discuss. It is about units for salt mass.
In this problem, the mass equation for salt is assumed to be written in kilograms.
But for it, the volume of water should be in liters.
So, the conversion factor gallons --> liters should be introduced.
But after introducing this factor, it will present, as a factor, in both sides
of the equation, and, therefore, can be reduced and omitted.
Then the final answer for the volume of water will be in gallons.
You should keep it in your mind, in order for the entire logical line
of the solution be correct in your head.
-----------------
On similar problems, see the lesson
- How much water must be evaporated
in this site.
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let water removed be x gallons
Initial quantity = 240 gallons , 3%
240*0.03 = (240-x)*0.05
7.2= 12-0,05x
4.8 = 0.05x
x =96
96 gallons of water must be evaporated to produce a 5% salt solution.
Question 1207753: The cooling system of a certain foreign-made car has a capacity of 15 liters. If the system is filled with a mixture that is 40% antifreeze, how much of this mixture should be drained and replaced by pure antifreeze so that the system is filled with a solution that is 60% antifreeze?
Let me see.
Mixture 1 + mixture 2 = total mixture
15(0.40) + x = 0.60(x + 15)
Is this the correct set up?
Found 3 solutions by greenestamps, ikleyn, josgarithmetic:
Answer by greenestamps(13215)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Your setup is NOT correct.
Your setup says you are mixing 15 liters of 40% antifreeze with an unknown amount of pure (100%) antifreeze to get (15+x) liters of 60% antifreeze.
The capacity of the cooling system is 15 liters, so that can't be right.
The x liters of pure antifreeze can only be put into the cooling system after x liters of the 40% antifreeze is drained out. So you are mixing (15-x) liters of the 40% antifreeze with x liters of pure antifreeze to get 15 liters of 60% antifreeze:
(15-x)(.40)+x(1.00)=15(.60)
Solve as shown in the response from the other tutor.
If formal algebra is not required, here is a solution using a quick and easy informal method that can be used to solve any 2-part mixture problem like this.
You are mixing 40% antifreeze with 100% antifreeze to get 60% antifreeze.
Look at the three percentages (on a number line, if it helps) and observe that 60% is 1/3 of the way from 40% to 100%.
That means 1/3 of the mixture needs to be the higher percentage antifreeze.
1/3 of 15 liters is 5 liters, so the mixture needs to use 5 liters of pure antifreeze. That of course means 5 liters of the 40% antifreeze must be drained to make room for the pure antifreeze.
ANSWER: 5 liters
Answer by ikleyn(52907)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The cooling system of a certain foreign-made car has a capacity of 15 liters.
If the system is filled with a mixture that is 40% antifreeze, how much of this mixture should be drained
and replaced by pure antifreeze so that the system is filled with a solution that is 60% antifreeze?
Let me see.
Mixture 1 + mixture 2 = total mixture
15(0.40) + x = 0.60(x + 15)
Is this the correct set up?
~~~~~~~~~~~~~~~~~~~~~~
Your setup equation is INCORRECT.
This problem is a standard and typical mixture problem.
To see many similar problems solved with detailed explanations, look into the lessons
- Word problems on mixtures for antifreeze solutions
in this site. Learn the subject from there.
/\/\/\/\/\/\/\/\/\/\/\/
Here I will show you very uncommon method of solution,
which allows to solve the problem practically MENTALLY.
The amount of the pure antifreeze in 15 liters of the 40% mixture
is 0.4*15 = 6 liters.
The amount of the pure antifreeze in 15 liters of the 60% mixture
is 0.6*15 = 9 liters.
So, the original mixture contained 6 liters of the pure antifreeze;
the final mixture contains 9 liters of the pure antifreeze.
Now, Let V be the volume of the mixture to replace.
When we drain V liters of the 40% mixture, 0.4*V liters of the pure antifreeze go out.
We replace it with V liters of the pure antifreeze.
So, V should be 3 liters more than 0.4V, which means
V - 0.4V = 3, or 0.6V = 3, hence V =  = 5 liters.
At this point, the solution is complete, and we get the
ANSWER. 5 liters of the of the original 40% mixture should be drained
and replaced by 5 liters of pure antifreeze. = 5 liters.
At this point, the solution is complete, and we get the
ANSWER. 5 liters of the of the original 40% mixture should be drained
and replaced by 5 liters of pure antifreeze.
Solved in full and explained completely.
------------------
Re-phrasing O'Henry, the famous American writer,
The blind begin to walk and the dumb begin to see
when they receive such beautiful solutions to their problems.
There is nothing here except a mind game.
Answer by josgarithmetic(39630)  (Show Source): (Show Source):
Question 1207745: A candy store sells boxes of candy containing caramels and cremes.Each box sells for $12.50 and holds 30 pieces of candy (all pieces are the same size).If the caramels cost $0.25 to produce and the cremes cost $0.45 to produce,how many of each should be in a box to make a profit of $3?
Found 3 solutions by mccravyedwin, greenestamps, mananth:
Answer by mccravyedwin(409)   (Show Source): (Show Source):
Answer by greenestamps(13215)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Here is a solution by an informal method that can be used to solve any 2-part "mixture" problem like this (if formal algebra is not required).
To make a profit of $3 on each box if the selling price is $12.50, the cost of production needs to be $12.50-$3 = $9.50.
The cost of producing 30 caramels would be 30($0.25) = $7.50; the cost of producing 30 cremes would be 30($0.45) = $13.50.
Use mental arithmetic to see that $9.50 is 1/3 of the way from $7.50 to $13.50.
That means 1/3 of the candies should be the more expensive cremes.
1/3 of 30 is 10.
ANSWER: 10 cremes and 20 caramels
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let number of caramelsbe x
and number of cremes in the box be y
Candies in each box = 30
x+y=30
The caramels cost $0.25 to produce and the cremes cost $0.45
One box sold for $12.50
Profit goal $3.00
Cost should be $9.50
Cost of candies equation
0.25x+0.45y=9.50
Multiply equation by 4
x+1.80y =38
x+y=30
Subtract the equations
0.80y =8
y=10
x=20
each box should contain:
20 caramels
10 cremes
Question 1207744: A coffee manufacturer wants to market a new blend of coffee that sells for $3.90 per pound by mixing two coffees that sell for $2.75 and $5 per pound,respectively.What amounts of each coffee should be blended to obtain the desired mixture?
[Hint:Assume that the total weight of the desired blend is 100 pounds.]
Let me see.
Let x = one type of coffee
Let y = another type of coffee
Here is my set up:
a + b = 100
2.75a + 5.00b = 100(3.90)
Is this correct?
Answer by ikleyn(52907)   (Show Source): (Show Source):
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085, 5086..5130, 5131..5175, 5176..5220, 5221..5265, 5266..5310, 5311..5355, 5356..5400, 5401..5445, 5446..5490, 5491..5535, 5536..5580, 5581..5625, 5626..5670, 5671..5715, 5716..5760, 5761..5805, 5806..5850, 5851..5895, 5896..5940, 5941..5985, 5986..6030, 6031..6075, 6076..6120, 6121..6165, 6166..6210, 6211..6255, 6256..6300, 6301..6345, 6346..6390, 6391..6435, 6436..6480, 6481..6525, 6526..6570, 6571..6615, 6616..6660, 6661..6705, 6706..6750, 6751..6795, 6796..6840, 6841..6885, 6886..6930, 6931..6975, 6976..7020, 7021..7065, 7066..7110, 7111..7155, 7156..7200, 7201..7245, 7246..7290, 7291..7335, 7336..7380, 7381..7425, 7426..7470, 7471..7515, 7516..7560, 7561..7605, 7606..7650, 7651..7695, 7696..7740, 7741..7785, 7786..7830, 7831..7875, 7876..7920, 7921..7965, 7966..8010, 8011..8055, 8056..8100, 8101..8145, 8146..8190, 8191..8235, 8236..8280, 8281..8325, 8326..8370, 8371..8415, 8416..8460, 8461..8505, 8506..8550, 8551..8595, 8596..8640, 8641..8685, 8686..8730, 8731..8775, 8776..8820, 8821..8865, 8866..8910, 8911..8955, 8956..9000, 9001..9045, 9046..9090, 9091..9135, 9136..9180, 9181..9225, 9226..9270, 9271..9315, 9316..9360, 9361..9405, 9406..9450, 9451..9495, 9496..9540, 9541..9585, 9586..9630, 9631..9675, 9676..9720, 9721..9765, 9766..9810, 9811..9855, 9856..9900, 9901..9945, 9946..9990, 9991..10035, 10036..10080, 10081..10125, 10126..10170, 10171..10215, 10216..10260, 10261..10305, 10306..10350, 10351..10395, 10396..10440, 10441..10485, 10486..10530, 10531..10575, 10576..10620, 10621..10665, 10666..10710, 10711..10755, 10756..10800, 10801..10845, 10846..10890, 10891..10935, 10936..10980, 10981..11025, 11026..11070, 11071..11115, 11116..11160, 11161..11205, 11206..11250, 11251..11295, 11296..11340, 11341..11385, 11386..11430, 11431..11475, 11476..11520, 11521..11565, 11566..11610, 11611..11655, 11656..11700, 11701..11745, 11746..11790, 11791..11835, 11836..11880, 11881..11925, 11926..11970, 11971..12015, 12016..12060, 12061..12105, 12106..12150, 12151..12195, 12196..12240, 12241..12285, 12286..12330, 12331..12375, 12376..12420, 12421..12465, 12466..12510, 12511..12555, 12556..12600, 12601..12645, 12646..12690, 12691..12735, 12736..12780, 12781..12825, 12826..12870, 12871..12915, 12916..12960, 12961..13005, 13006..13050, 13051..13095, 13096..13140, 13141..13185, 13186..13230, 13231..13275, 13276..13320, 13321..13365, 13366..13410, 13411..13455, 13456..13500, 13501..13545, 13546..13590, 13591..13635, 13636..13680, 13681..13725, 13726..13770, 13771..13815, 13816..13860, 13861..13905, 13906..13950, 13951..13995, 13996..14040, 14041..14085, 14086..14130, 14131..14175, 14176..14220, 14221..14265, 14266..14310, 14311..14355, 14356..14400, 14401..14445, 14446..14490, 14491..14535, 14536..14580, 14581..14625, 14626..14670, 14671..14715, 14716..14760, 14761..14805, 14806..14850, 14851..14895, 14896..14940, 14941..14985, 14986..15030, 15031..15075, 15076..15120, 15121..15165, 15166..15210, 15211..15255, 15256..15300, 15301..15345, 15346..15390, 15391..15435, 15436..15480, 15481..15525, 15526..15570, 15571..15615, 15616..15660, 15661..15705, 15706..15750, 15751..15795, 15796..15840, 15841..15885, 15886..15930, 15931..15975, 15976..16020, 16021..16065, 16066..16110, 16111..16155, 16156..16200, 16201..16245
|





