Question 988199: Two cyclists, 168 mi apart, start riding towards each other at the same time. One cycles twice as fast as the other. If they meet 4 hr later, at what average speed is each cyclist traveling?
Found 3 solutions by solver91311, macston, ikleyn:
Answer by solver91311(24713)   (Show Source): (Show Source):
Answer by macston(5194)   (Show Source): (Show Source):
You can put this solution on YOUR website! They traveled 168 miles in 4 hours, so the sum of their speeds was:
168 miles/4 hours=42 miles an hour
.
S=Slower cycler's speed; F=faster cycler's speed=2S
.
S+F=42mph
S+2S=42mph
3S=42mph
S=14mph
ANSWER 1: The slower cyclist's speed was 14 mph.
.
F=2S=2(14mph)=28 mph
ANSWER 2: The faster cyclist's speed was 28 mph.
.
CHECK:
4(S)+4(F)=168 miles
4hrs(14mph)+4hrs(28mph)=168 miles
56 miles + 112 miles=168 miles
168 miles=168 miles
Answer by ikleyn(52802)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let x be the average speed of the slower cyclist, in mph (miles per hour).
Then the average speed of the other cyclist is 2x mph, according to the condition.
Since the two cyclists are riding towards each other, their relative rate is
x + 2x = 3x mph.
So, the distance between the cyclists decreases in 3x miles each hour. Since they met 4 hours later, the distance they both covered was 4*3x = 12x miles.
It is exactly the distance between their starting points, i.e. 168 mi. So, you have an equation
12x = 168,
which gives x = 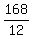 = 14 mph. = 14 mph.
Hence, the average speed of the slower cyclist is 14 mph, and that of the other cyclist is 2*14 = 28 mph.
The problem is solved.
|
|
|