Question 971976: find the area of the largest trapezoid that can be inscribed a semicircle of diameter "d" in terms of "d"?. what is the length of the bottom base "x" of the same trapezoid ??
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! In the American definition, a trapezoid has two parallel sides  . .
I am assuming that the drawing above shows what was meant: a trapezoid inscribed in a semicircle.
Intuitively, we could assume that the largest polygon that can be inscribed in a circle is the regular polygon of its kind,
so that the largest inscribed triangle would be an equilateral triangle,
the largest quadrilateral would be a square,
the largest pentagon a regular pentagon,
the largest hexagon a regular hexagon, and so on.
If that is so, the largest trapezoid inscribed in a semicircle may be half of a hexagon.
That trapezoid would have base angles measuring  , ,
and could be thought of as made of three equilateral triangles:  . .
In a semicircle of radius  ,the area of that trapezoid is ,the area of that trapezoid is
 . .
There may be a very simple proof supporting that maximum area value,
but I was taught a lot of math past the fifth grade, and that spoiled me forever,
so I can only offer a complicated proof or two.
I just cannot think of a proof that does not involve calculus.
 . .
Using  : :







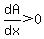 between both roots of between both roots of  <---> <--->
Solving that quadratic equation we realize that the solutions are
 (which, making (which, making  does not make sense, and does not make sense, and
 , which makes sense and makes , which makes sense and makes  , ,
marking the maximum for  . .
So, that maximum is







Using 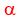 : :
The trapezoid is made of three isosceles triangles.
They have legs of length  , ,
and vertex angles measuring 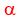 , , 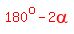 , and , and 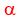 . .
The area of the trapezoid is the sum of the triangles' areas, so it is









 for for 
and  between both roots, between both roots,
so 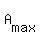 happens for the greatest root of happens for the greatest root of  . .
Making  for short, the equation is for short, the equation is
 and the roots are and the roots are


The roots are  , ,
so  increases with increases with  , ,
between  <--> <--> , and , and
 <--> <--> , ,
and the maximum is at  <--> <--> , where , where





 , ,

|
|
|