Question 66598: a man put a pair of youngster rabbits(January 1st) in aplace surrounded by a wall. This pair of rabbits will have to wait one month to become adults before having their litter of baby rabbits. the litter of rabbits will have to wait one month before being youngster and an additional month before they are adults and have their own litter of rabbits. Assume that each new litter consists of a male and famale pair, and the rabbits never die. How many pairs of rabbits can be produced from the original pair in ayear if it is supposed that every month each pair has a new pair which from the second month on becomes productive? your results should be presented in a format that can be easily read, followed, amd understood. Explain your results.
Answer by Nate(3500)   (Show Source): (Show Source):
You can put this solution on YOUR website! I will not do your assignment paper persay ... but I will tell you some interesting facts.
y = youngster .... a = adults
Pairs are counted as Adult Pairs:
initial time: 1y ~> 0 (a) pairs
1 month: 1a ~> 1 (a)pair (give birth to 1y)
2 months: 1a1y ~> 1 (a)pair
3 months: 2a1y ~> 2 (a)pairs
4 months: 3a2y ~> 3 (a)pairs
5 months: 5a3y ~> 5 (a)pairs
6 months: 8a5y ~> 8 (a)pairs
7 months: 13a8y ~> 13 (a)pairs
8 months: 21a13y ~> 21 (a)pairs
9 months: 34a21y ~> 34 (a)pairs
10 months: 55a34y ~> 55 (a)pairs
11 months: 89a55y ~> 89 (a)pairs
12 months: 144a89y ~> 144 (a)pairs
0,1,1,2,3,5,8,13,21,34,55,89,144....
See a pattern or do you already know the series? It is the Fibonacci Series where the sum of the two previous numbers is the equivalent to the third. This series gives birth to a number that is thought as sacred or golden (a.k.a. the golden number.)
Define as one of the Fib. numbers as 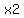 and the previous number to be and the previous number to be 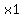 . .
As 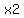 approaches infinity: approaches infinity: 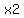 / /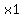 = Golden Number = 1.618033.... = Golden Number = 1.618033....
 = = 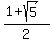 = 1.618033.... = 1.618033....
|
|
|