Question 661971: PLEASE HELP!!!ASAP!! When mixed, a 12 ounce can of concentrate makes 64 ounces of orange juice. If each serving is 8 ounces, explain & find the number of cans of concentrate needed to make 240 servings.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! One can makes 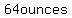 , which amounts to , which amounts to
 servings servings
(We are dividing those 64 ounces into 8 ounce servings and get 8 servings).
Since one can produces 8 servings, 240 servings will require
 cans cans
(We are dividing the 240 servings 8 servings amounts, which we know is what comes out of one can).
I am hoping that is considered enough of an explanation.
If I had been in your class, I could guess what your teacher expects.
If more explanation is needed, I have 2 ideas:
Multiplications are easy to use and understand.
It is easy to see that ounces per serving.
multiplied times number of servings,
gives total amount in ounces.
It is harder to figure out that when you know the product of that multiplication
(the total amount in ounces),
and one of the factors (ounces per serving or number of servings),
you need to divide by the known factor to find the other factor.
Division is the inverse operation of multiplication,
and since it takes two numbers/factors to get a multiplication,
it is associated with two divisions.
If you consider number of cans, servings per can, and total number of servings,
having two of those three pieces of information, we should be able to find the third one.
To find how many servings we can get if we use  cans and each can makes cans and each can makes  servings, we multiply. servings, we multiply.
If you get  servings per can, and use servings per can, and use  cans, cans,
you will make  servings. servings.
The divisions associated with that multiplication answer the two questions below.
How many servings can we get from each can if  cans produce cans produce  servings? servings?
 servings. servings.
How many cans do we need for  servings, if each can produces servings, if each can produces  servings? servings?
 servings. servings.
Maybe your teacher expects something like this:

where the "units" (servings, and ounces) appear in numerator and denominator, and seem to "cancel out", so the only "unit" left is "cans."
Sometimes teachers do that stuff (it's used a lot in chemistry), and they may even call it "dimensional analysis" or something like that.
|
|
|