SOLUTION: A shirt shop has 112 orders for t-shirt designs. Three designers can make 12 shirts in 2 hours. How many designers are needed to complete the orders in 8 hours? I am not a math

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: A shirt shop has 112 orders for t-shirt designs. Three designers can make 12 shirts in 2 hours. How many designers are needed to complete the orders in 8 hours? I am not a math      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 639081: A shirt shop has 112 orders for t-shirt designs. Three designers can make 12 shirts in 2 hours. How many designers are needed to complete the orders in 8 hours?
I am not a math person, at all. I would be very much obliged if whoever can solve this problem would explain it to me in a VERY simple way. :)
Found 2 solutions by Edwin McCravy, MathTherapy:
Answer by Edwin McCravy(20055) About Me  (Show Source):
You can put this solution on YOUR website!
A shirt shop has 112 orders for t-shirt designs. Three designers can make 12 shirts in 2 hours. How many designers are needed to complete the orders in 8 hours?
First way:

3 designers can make 12 shirts in 2 hours

therefore since 8=4*2 and 4*12=48  

3 designers can make 48 shirts in 8 hours

therefore since 3÷3=1 and 48÷3=16

1 designer can make 16 shirts in 8 hours

therefore since 112=16*7 and 1*7=7

7 designers can make 112 shirts in 8 hours


Second way:

Use the worker-time-job formula, which is:

%28W%5B1%5DT%5B1%5D%29%2FJ%5B1%5D%22%22=%22%22%28W%5B2%5DT%5B2%5D%29%2FJ%5B2%5D

where

W1 = the number of workers in the first situation.
T1 = the number of time units (hours in this case) in the first situation.
J1 = the number of jobs in the first situation.

W2 = the number of workers in the second situation.
T2 = the number of time units (hours in this case) in the second situation.
J2 = the number of jobs in the second situation.

W1 =  3             W2 = the unknown quantity     
T1 =  2             T2 = 8 
J1 = 12             J2 = 112

%28W%5B1%5DT%5B1%5D%29%2FJ%5B1%5D%22%22=%22%22%28W%5B2%5DT%5B2%5D%29%2FJ%5B2%5D

%283%2A2%29%2F12%22%22=%22%22%28W%5B2%5D%2A8%29%2F112

6%2F12%22%22=%22%22%288W%5B2%5D%29%2F112

6%2F12 reduces to 1%2F2 and 8%2F112 reduces to 1%2F14

1%2F2%22%22=%22%22%28W%5B2%5D%29%2F14

Cross-multiply

2W2 = 14

Divide both sides by 2

 W2 = 7

Answer: 7 workers.

Edwin

Answer by MathTherapy(10552) About Me  (Show Source):
You can put this solution on YOUR website!

A shirt shop has 112 orders for t-shirt designs. Three designers can make 12 shirts in 2 hours. How many designers are needed to complete the orders in 8 hours?

The amount of designers vary DIRECTLY with the amount of work to be done, but vary INDIRECTLY, or INVERSELY to the amount of time needed. In other words, the more work to be done the more designers are required, hence the DIRECT variation. On the other hand, the greater amount of designers used to design the t-shirts, the less time it'll take to complete the job.

Having said that, we use the formula combining DIRECT and INDIRECT variations, as follows:

d = k(j)/T, with:
d being the amount of designers
k being the constant of variation
j being the units of the job
T being time

Applying the fact that 3 designers are needed to complete 12 t-shirts in 2 hours, we can determine k, the constant of variation.

d+=+k%28j%29%2FT

3+=+k%2812%29%2F2

3+=+12k%2F2

12k = 6 ------ Cross-multiplying

k = 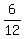6%2F12, or 1%2F2

With d+=+%281%2F2%29j%2FT, and with k = 1%2F2; j (jobs) = 112; and T (time) = 8, we get:
d+=+%281%2F2%29%28112%29%2F8

d+=+56%2F8

d, or amount of designers needed to complete 112 t-shirts in 8 hours = highlight_green%287%29

Send comments and “thank-yous” to “D” at MathMadEzy@aol.com