Question 135094: An arrow is shot vertically upward with an initial velocity of 250 feet per second from an initial height of 10 feet. The height of the arrow as a function of the time t in seconds, is given by the function s(t)=-16t^2+150t+10. Solve each of the following analytically.
a. what is the height of the arrow after 2 seconds
b. What is the maximum height reached by the arrow
c. After how many seconds will the arrow return to the ground
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! The first thing is that either the initial velocity you have given is incorrect, or the function is incorrectly written. The coefficient on the t term must be equal to the initial velocity. Unfortunately, both 250 fps and 150 fps are within a resonable range for modern archery equipment. So, I'm going to chose to believe that the function is correct. If it is the other way around, you will have to modify things to fit.
a. The height after 2 seconds: Evaluate 
b. The maximum height:
Two ways to do this.
The algebra way: This is a parabola with a vertex at (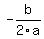 , ,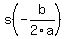 ). ).  , so evaluate , so evaluate  to find the maximum height. to find the maximum height.
The calculus way: Take the first derivative of the function:
 , set the first derivative equal to zero and solve: , set the first derivative equal to zero and solve:


Again, evaluate:  to find the maximum height. to find the maximum height.
c. The arrow will be on the ground when s(t) = 0. So solve  for t. You will get two roots, one of which will be negative (that's because the arrow started out 10 feet up, and it would be negative time when it was on the ground prior to getting up to 10 ft). Discard the negative root and the positive root is the answer. for t. You will get two roots, one of which will be negative (that's because the arrow started out 10 feet up, and it would be negative time when it was on the ground prior to getting up to 10 ft). Discard the negative root and the positive root is the answer.
|
|
|