Question 1201551: The radioactive isotope of potassium-42, which is a vital in the diagnosis of brain tumors, has a half life of 12.36 hours.
Determine the exponential decay model that represents the mass of potassium-42?
Found 3 solutions by josgarithmetic, mananth, ikleyn:
Answer by josgarithmetic(39617)   (Show Source):
Answer by mananth(16946)  (Show Source):
You can put this solution on YOUR website!
We use the formula of exponential decay.
P = P0 e-^(kt)
P0 = initial amount of Potassium
half-life of Potassium is 12.36 hours.
P = P0 / 2 = Half of the amount of K-42 when t = 12.36.
Substitute all these values in the formula of exponential decay
P0 / 2 =P0 e-^ k (12.36) P0 cancels off
0.5 = e- k (12.36)
Taking "ln" on both sides,
ln 0.5 = -12.36k
k = ln 0.5 / (-12.36) ≈ 0.056
P = P0* e- 0.056t
Plug the values
P=500*e^(-0.056*48)
P =34.008 mg
Other simple method
half life = 12.36
Time = 48
There are 48/12.36 half lives in 48 hours = 3.88
Amount remaining = 500/2^3.88
= 33.96 mg
Answer by ikleyn(52781)  (Show Source):
You can put this solution on YOUR website! .
The radioactive isotope of potassium-42, which is a vital in the diagnosis of brain tumors,
has a half life of 12.36 hours.
Determine the exponential decay model that represents the mass of potassium-42?
~~~~~~~~~~~~~~~~~~~~~~
As soon as the half-life time period is given as numerical value of T,
the standard exponential decay formula is
m(t) =  ,
where m(0) is the starting mass at t= 0 and m(t) is remaining mass in the current time moment t.
In your case, the exponential model is
m(t) =  ,
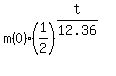t is the time in hours.
If the problem is formulated as it is in this post, there is NO any need to use (ekt)-model.
The exponential model with the base (1/2) is what they expect to get from you as an answer, in this case.
Solved, answered and explained.
-----------------
On radioactive decay, see the lesson
- Radioactive decay problems
in this site.
You will find many similar (and different) solved problems there.
Use this lesson as your handbook, textbook, guide, tutorials, and (free of charge) home teacher.
Learn the subject from there once and for all.
/////////////////
I do not know why two other persons (@josgarithmetic and @mananth) started making some calculations.
This problem does not requires to make any calculations.
It only requires to write an exponential model.
These persons even do not read the problem and do not relate their writing to the problem.
Unfortunately.
|
|
|
