Question 1163258: 2/5's of A's money is equal to 2/3's of B's money. Total of their money is $4800. Determine A and B's money.
2/5 of A's = 2/3's of B's.
A + B = 4800.
Not sure how to proceed.
Found 3 solutions by Boreal, greenestamps, ikleyn:
Answer by Boreal(15235)   (Show Source):
You can put this solution on YOUR website! that's a good start
multiply the first by 15 to clear fractions
6A=10B
3A=5B. then A=(5/3) B, to bring a fraction back which can be more easily substituted.
A+B=4800
(5/3)B+B=4800. (5/3)+B is (5/3)B+(3/3)B, common denominator. They add to (8/3)B
(8/3)B=4800
B=4800*3/8=$1800
A=$3000
2/5 s of A is $1200
2/3s of B is $1200
Answer by greenestamps(13200)  (Show Source):
Answer by ikleyn(52797)  (Show Source):
You can put this solution on YOUR website! .
From the condition, you have
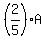 =  . (1)
Multiply both sides by 3*5 = 15. You will get
6A = 10B, or
3A = 5B. (2)
You have also second equation
A + B = 4800. (3)
Multiply its both sides by 3. You will get
3A + 3B = 3*4800 = 14400.
In the left side, replace 3A by 5B, based on equation (2). You will get
5B + 3B = 14400, or
8B = 14400,
B = 14400/8 = 1800.
So, the amount B is just found: it is 1800 dollars.
The last step is to find A. For it, subtract 1800 from 4800
A = 4800 - 1800 = 3000 dollars.
ANSWER. A has $3000; B has $1800.
-------------
comment from student: Why did you multiply equation (3) by 3 ?
-------------
My response : Good question, thanks for asking.
I multiply equation (3) by 3 in order for to have this term " 3A ", which I later replace by " 5B ".
My secret goal is to get an equation for one unknown " B " only, and for it I make all these transformations.
Is everything clear to you now ?
If you still have questions, do not hesitate to post them to me . . .
Have a nice day (!)
-------------
comment from student: How did you get 3A = 5B from 6A = 10B ?
-------------
My response : I divided both sides of the equation 6A = 10B by 2.
|
|
|
