Question 1085911: A farmer has 120 acres of land on which she plans to grow wheat and corn. Each acre of wheat requires 5 hours of labor and $20 of capital, and each acre of corn requires 15 hours of labor and $30 of capital. The farmer has at most 1500 hours of labor and $6000 of capital available. If the profit from an acre of wheat is $100 and from an acre of corn is $120, how many acres of each crop should she plant to maximize her profit?
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A farmer has 120 acres of land on which she plans to grow wheat and corn.
Each acre of wheat requires 5 hours of labor and $20 of capital,
and each acre of corn requires 15 hours of labor and $30 of capital.
The farmer has at most 1500 hours of labor and $6000 of capital available.
If the profit from an acre of wheat is $100 and from an acre of corn is $120,
how many acres of each crop should she plant to maximize her profit?
~~~~~~~~~~~~~~~~~~
Let X be the area for wheat (in acres), and
let Y be the area for corn.
The amount of labor is 5X + 15Y hours.
The amount of capital is 20X + 30Y dollars.
The constraints are
5x + 15Y <= 1500 (1) (hours)
20X + 30Y <= 6000 (2) (dollars)
X >= 0, (3)
Y >= 0. (4)
The profit function is P(X,Y) = 100X + 120Y. (5)
So, the problem is to maximize (5) under restrictions (1) - (4).
The feasibility area (1) - (4) is shown in the figure below.
 Plots y =
Plots y = 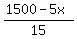 (red) and y = (red) and y = 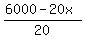 (green)
The feasibility area is the intersection of two right-angled triangles: one with red hypotenuse (restrictions (1),(3),(4))
and the other with green hypotenuse (restrictions (2),(3),(4)).
The intersection is the smaller right-angled triangle,
and to get the solution of the minimax problems, you should compare the profit function at two points: (X,Y) = (0,100) and (X,Y) = (300,0).
P(0,100) = 100*0 + 120*100 = 12000 dollars,
P(300,0) = 100*300 + 120*0 = 30000 dollars.
The larger value is at the point (X,Y) = (300,0).
So the solution is (X,Y) = (300,0), i.e. 300 acres for wheat and 0 acres for corn.
The profit value expected/predicted is $30000. (green)
The feasibility area is the intersection of two right-angled triangles: one with red hypotenuse (restrictions (1),(3),(4))
and the other with green hypotenuse (restrictions (2),(3),(4)).
The intersection is the smaller right-angled triangle,
and to get the solution of the minimax problems, you should compare the profit function at two points: (X,Y) = (0,100) and (X,Y) = (300,0).
P(0,100) = 100*0 + 120*100 = 12000 dollars,
P(300,0) = 100*300 + 120*0 = 30000 dollars.
The larger value is at the point (X,Y) = (300,0).
So the solution is (X,Y) = (300,0), i.e. 300 acres for wheat and 0 acres for corn.
The profit value expected/predicted is $30000.
Solved.
To see more minimax problems/samples solved, look into the lesson
- Solving minimax problems by the Linear Programming method
in this site.
|
|
|