|
Question 1183382: Let n ∈ N and B be a n × n matrix that has determinant 1. Show that there exist n × n matrices
K, A and N with the following four properties:
(a) B = KAN,
(b) K is an orthogonal matrix with det(K) = 1,
(c) N is an upper triangular matrix with all diagonal entries 1; and
(d) A is a diagonal matrix whose all diagonal entries are positive and det(A) = 1
Answer by robertb(5830)   (Show Source):
You can put this solution on YOUR website! The LU decomposition of B states that B = LU where L is a lower triangular matrix and U is an upper triangular matrix.
An even better decomposition is the LU decomposition with partial pivoting, which says that
for some permutation matrix P. One property of permutation matrix is that it is always orthogonal, i.e.,  .
In other words,
 , or its transpose is its own inverse.
Hence, 
Note that by symmetry,  is also orthogonal.
Now none of the diagonal elements of U is equal to 0, since the determinant of B is 1. This implies that U can be decomposed into
 ,
where diag(U) is a diagonal matrix whose diagonal elements and their locations are the same as those of U,
and 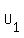 is an upper triangular matrix where all diagonal elements are 1.
Now  , or  where Q is a permutation matrix that turns L into an upper triangular matrix  .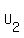
==>  .
Similarly,  , where 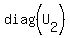 is a diagonal matrix whose diagonal elements and their locations are the same as those of ,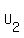
and 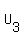 is an upper triangular matrix where all diagonal elements are 1.
==>  .
where 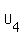 is still an upper triangular matrix with diagonal elements equal to 1.
==>  .
Now  , because its rows are just rearrangements of the rows of I;
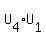 is an upper triangular matrix whose diagonal elements are all 1, hence its determinant is equal to 1;
and finally 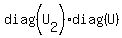 has the same determinant as LU, and therefore equal to 1.
Hence, let  ,  , and  , and the statement is proved.
|
|
|
| |
