|
Tutors Answer Your Questions about Matrices-and-determiminant (FREE)
Question 1159507: Find a non-zero 2×2 matrix such that:
[-9, -3] * [] = [0, 0]
[18, 6] [] [0, 0]
Answer by ikleyn(52858)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find a non-zero 2×2 matrix such that:
[-9, -3] * [] = [0, 0]
[18, 6] [] [0, 0]
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Looking at the first (2x2)-matrix, you may notice that its first column is three times the second column.
It tells you to take the first column of the second (2x2)-matrix as  .
Looking again at the first (2x2)-matrix, you may notice that its second column is one third times the first column.
It tells you to take the second column of the second (2x2)-matrix as .
Looking again at the first (2x2)-matrix, you may notice that its second column is one third times the first column.
It tells you to take the second column of the second (2x2)-matrix as 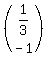 .
Thus, the second matrix can be taken as .
Thus, the second matrix can be taken as 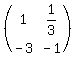 .
Now you may check, making handle calculations, that .
Now you may check, making handle calculations, that
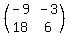 * *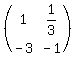 = = 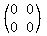 , QED. , QED.
This way, the problem is just solved, and one instance matrix is found.
But this solution is not a unique.
Every other matrix, c-times the found, where 'c' is any non-zero constant value, has the same property.
Question 1159895: Find a basis of the subspace of R^4 defined by the equation −5x1−5x2−4x3−8x4=0.
Answer by ikleyn(52858)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find a basis of the subspace of R^4 defined by the equation −5x1−5x2−4x3−8x4=0.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
(1) From general theory, the dimension of this subspace is 4-1 = 3.
So, we need to find three basic vectors.
(2) It is enough to find three linearly independent vectors, satisfying the given equation.
(3) For simplicity, we can use an EQUIVALENT equation instead of the given one
5x1 + 5x2 + 4x3 + 8x4 = 0. (1)
(4) First such vector is V1 = (1, -1, 0, 0).
You can check that this vector satisfies equation (1).
(5) Second such vector is V2 = (1, 0, -1.25, 0). The component -1.25 is -5/4.
You can check that this vector satisfies equation (1).
(6) Third such vector is V3 = (1, 0, 0, -0.6125). The component -0.6125 is -5/8.
You can check that this vector satisfies equation (1).
(7) Finally, it is obvious that vectors V1, V2 and V3 are linearly independent,
so vectors V1, V2 and V3 provide the solution to the problem. ANSWER
Solved.
Question 1159842: Find a basis of the subspace of R4 defined by the equation −5x1−5x2−4x3−8x4=0.
Answer by ikleyn(52858)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find a basis of the subspace of R^4 defined by the equation −5x1−5x2−4x3−8x4=0.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
(1) From general theory, the dimension of this subspace is 4-1 = 3.
So, we need to find three basic vectors.
(2) It is enough to find three linearly independent vectors, satisfying the given equation.
(3) For simplicity, we can use an EQUIVALENT equation instead of the given one
5x1 + 5x2 + 4x3 + 8x4 = 0. (1)
(4) First such vector is V1 = (1, -1, 0, 0).
You can check that this vector satisfies equation (1).
(5) Second such vector is V2 = (1, 0, -1.25, 0). The component -1.25 is -5/4.
You can check that this vector satisfies equation (1).
(6) Third such vector is V3 = (1, 0, 0, -0.6125). The component -0.6125 is -5/8.
You can check that this vector satisfies equation (1).
(7) Finally, it is obvious that vectors V1, V2 and V3 are linearly independent,
so vectors V1, V2 and V3 provide the solution to the problem. ANSWER
Solved.
Question 1165621: Solve the system:
{4x1+x2=7
{12x1+3x2=21
[x1]=[]+s[]
[x2]=[]+s[]
Answer by ikleyn(52858)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Solve the system:
{4x1+x2=7
{12x1+3x2=21
[x1]=[]+s[]
[x2]=[]+s[]
~~~~~~~~~~~~~~~~~~~~~~~
In this assignment, the second equation is 3 times first equation.
So, actually, two equations of the given system are equivalent to one equation
4x + y = 7.
The solution for this equation is
y = 7 - 4x.
It means that 'x' is a "free variable", which may have any value;
then the corresponding 'y' value is calculated as 7 - 4x.
In parametric form, we put
x = s,
y = 7 - 4s.
Thus we get the parametric solution to the given system of equations
in the form, which is requested in the assignment.
At this point, the problem is solved completely, with comprehensive explanations.
Question 1168173: Lanre income from interest and wages is 4000 he double his investment and also get an increase to 6500 my what was his original income separately in both term (interest and wages). Using crammer rules.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let $i$ be Lanre's original income from interest, and $w$ be his original income from wages.
From the first statement, his total original income is $4000:
Equation 1: $i + w = 4000$
From the second statement, he doubles his investment (which we assume directly doubles his interest income) and his total income becomes $6500. His wage income remains the same.
New interest income = $2i$
New wage income = $w$
New total income = $6500$
Equation 2: $2i + w = 6500$
We have a system of two linear equations with two variables:
1) $i + w = 4000$
2) $2i + w = 6500$
We will use Cramer's rule to solve this system. Cramer's rule states that for a system of linear equations:
$a_1x + b_1y = c_1$
$a_2x + b_2y = c_2$
The solutions for $x$ and $y$ are given by:
$x = \frac{D_x}{D}$
$y = \frac{D_y}{D}$
where $D$ is the determinant of the coefficient matrix, and $D_x$ and $D_y$ are the determinants of matrices formed by replacing the column corresponding to $x$ and $y$ respectively with the constant terms.
In our case, the variables are $i$ and $w$:
$1i + 1w = 4000$
$2i + 1w = 6500$
Here, $a_1 = 1, b_1 = 1, c_1 = 4000$ and $a_2 = 2, b_2 = 1, c_2 = 6500$.
First, calculate the determinant of the coefficient matrix $D$:
$D = \begin{vmatrix} 1 & 1 \\ 2 & 1 \end{vmatrix} = (1 \times 1) - (1 \times 2) = 1 - 2 = -1$
Next, calculate the determinant $D_i$ by replacing the first column (coefficients of $i$) with the constant terms:
$D_i = \begin{vmatrix} 4000 & 1 \\ 6500 & 1 \end{vmatrix} = (4000 \times 1) - (1 \times 6500) = 4000 - 6500 = -2500$
Now, calculate the determinant $D_w$ by replacing the second column (coefficients of $w$) with the constant terms:
$D_w = \begin{vmatrix} 1 & 4000 \\ 2 & 6500 \end{vmatrix} = (1 \times 6500) - (4000 \times 2) = 6500 - 8000 = -1500$
Finally, use Cramer's rule to find the values of $i$ and $w$:
$i = \frac{D_i}{D} = \frac{-2500}{-1} = 2500$
$w = \frac{D_w}{D} = \frac{-1500}{-1} = 1500$
So, Lanre's original income from interest was $2500, and his original income from wages was $1500.
Let's check if these values satisfy the given conditions:
Original total income: $2500 + 1500 = 4000$ (Correct)
Doubled investment (interest) and increased total income: $2(2500) + 1500 = 5000 + 1500 = 6500$ (Correct)
Final Answer: The final answer is $\boxed{Original interest income was $2500 and original wage income was $1500}$
Question 1169744: The general linear supply and demand for one-commodity market model are given by
P = a𝑄𝑠+b (a>0, b>0)
P = - c𝑄𝐷+d (c>0, d>0)
a. Show that in matrix notation the equilibrium price, P, and quantity, Q satisfy.
[1 −𝑎] [𝑃]=[𝑏]
1 𝑐 𝑄 𝑑
b. Solve this system to express P and Q in terms of a, b, c and d.
c. Write down the multiplier for Q due to changes in b and deduce that an increase in b lends to an decrease in Q.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Absolutely, let's solve this supply and demand problem.
**Understanding the Model**
We have a one-commodity market with linear supply and demand equations:
* Supply: P = aQs + b (a > 0, b > 0)
* Demand: P = -cQd + d (c > 0, d > 0)
Where:
* P = Price
* Qs = Quantity supplied
* Qd = Quantity demanded
At equilibrium, Qs = Qd = Q.
**a) Show the Matrix Notation**
1. **Rewrite the Equations:**
* Supply: P - aQ = b
* Demand: P + cQ = d
2. **Matrix Form:**
We can represent these equations in matrix form:
```
[ 1 -a ] [ P ] = [ b ]
[ 1 c ] [ Q ] = [ d ]
```
Thus, we have shown the required matrix equation.
**b) Solve for P and Q**
1. **Matrix Equation:**
Let:
```
A = [ 1 -a ]
[ 1 c ]
X = [ P ]
[ Q ]
B = [ b ]
[ d ]
```
We have AX = B, so X = A⁻¹B.
2. **Inverse of A:**
* det(A) = (1 * c) - (-a * 1) = c + a
* A⁻¹ = (1 / (c + a)) * [ c a ]
[ -1 1 ]
3. **Solve for X (P and Q):**
```
[ P ] = (1 / (c + a)) * [ c a ] [ b ]
[ Q ] [ -1 1 ] [ d ]
```
```
P = (1 / (c + a)) * (cb + ad) = (cb + ad) / (c + a)
Q = (1 / (c + a)) * (-b + d) = (d - b) / (c + a)
```
Therefore:
* P = (cb + ad) / (c + a)
* Q = (d - b) / (c + a)
**c) Multiplier for Q due to Changes in b**
1. **Q in terms of b:**
* Q = (d - b) / (c + a)
2. **Multiplier:**
The multiplier for Q due to changes in b is the derivative of Q with respect to b:
* dQ/db = -1 / (c + a)
3. **Deduction:**
Since a > 0 and c > 0, (c + a) > 0. Therefore, -1 / (c + a) is always negative.
This means that an increase in b (the y-intercept of the supply curve) leads to a decrease in Q (the equilibrium quantity).
**Final Answers**
* **(a)** The matrix notation is: [ 1 -a ] [ P ] = [ b ]
[ 1 c ] [ Q ] = [ d ]
* **(b)** P = (cb + ad) / (c + a)
Q = (d - b) / (c + a)
* **(c)** The multiplier for Q due to changes in b is -1 / (c + a). Since this is negative, an increase in b leads to a decrease in Q.
Question 1171379: An architect has a pool in the floor plans for a home. Set up a determinant that gives the unit area of the pool. Coordinates given: (4,4) (1, -5) (-5, -3)
Found 3 solutions by ikleyn, timofer, josgarithmetic:
Answer by ikleyn(52858)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The person who created this "problem", has the skills to create tales
for 3 - 5 years old children, but has no skills to create Math problems.
Answer by timofer(105)  (Show Source): (Show Source):
You can put this solution on YOUR website! If you try to graph those given points and, assuming there is one missing point as part of a parallelogram, then accounting for the slopes of (-5,-3) & (1,-5), and (4,4) & (1,-5), then the missing point would be (-1,-6).
Still too much seems omitted from your problem description.
Taking another look at just what is described and is asked, maybe these would help:
https://www.triangle-calculator.com/?what=vc
https://www.omnicalculator.com/math/area-triangle-coordinates
https://ncalculators.com/geometry/triangle-area-by-3-points.htm
The area is 30 units.
Answer by josgarithmetic(39626)  (Show Source): (Show Source):
You can put this solution on YOUR website! Too much missing here. Three points? For a triangle? Or is another point missing, maybe for a rectangle? Where is other length or scaling information?
Question 1175738: If point A = matrices 4 -4 -3 and B = 2 0 2 . Then find AB and BA
0 0 -2 2 -2 1
1 -4 -2 -1 -1 -2
I tried the following. I am not sure how to get the other numbers.
4x2 + -4x2 + -3x-1=3
0x0 + 0x-2 + -2x-1=-2
1x2 + -4x1 + -2x-2=2
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! You're on the right track with matrix multiplication! Let's break down how to calculate AB and BA step-by-step.
**Matrix Multiplication (AB)**
* **Dimensions:** First, check if the multiplication is possible. Matrix A is a 3x3 matrix, and matrix B is also a 3x3 matrix. Since the number of columns in A matches the number of rows in B, we can multiply them. The result will be a 3x3 matrix.
* **Calculation:**
* To get the element in the first row and first column of AB, you multiply the first row of A by the first column of B:
* (4 * 2) + (-4 * 2) + (-3 * -1) = 8 - 8 + 3 = 3 (You got this one right!)
* To get the element in the first row and second column of AB, you multiply the first row of A by the second column of B:
* (4 * 0) + (-4 * -2) + (-3 * -1) = 0 + 8 + 3 = 11
* To get the element in the first row and third column of AB, you multiply the first row of A by the third column of B:
* (4 * 2) + (-4 * 1) + (-3 * -2) = 8 - 4 + 6 = 10
* To get the element in the second row and first column of AB, you multiply the second row of A by the first column of B:
* (0 * 2) + (0 * 2) + (-2 * -1) = 0 + 0 + 2 = 2
* To get the element in the second row and second column of AB, you multiply the second row of A by the second column of B:
* (0 * 0) + (0 * -2) + (-2 * -1) = 0 + 0 + 2 = 2
* To get the element in the second row and third column of AB, you multiply the second row of A by the third column of B:
* (0 * 2) + (0 * 1) + (-2 * -2) = 0 + 0 + 4 = 4
* To get the element in the third row and first column of AB, you multiply the third row of A by the first column of B:
* (1 * 2) + (-4 * 2) + (-2 * -1) = 2 - 8 + 2 = -4
* To get the element in the third row and second column of AB, you multiply the third row of A by the second column of B:
* (1 * 0) + (-4 * -2) + (-2 * -1) = 0 + 8 + 2 = 10
* To get the element in the third row and third column of AB, you multiply the third row of A by the third column of B:
* (1 * 2) + (-4 * 1) + (-2 * -2) = 2 - 4 + 4 = 2
* **Result (AB):**
```
AB = | 3 11 10 |
| 2 2 4 |
| -4 10 2 |
```
**Matrix Multiplication (BA)**
* **Dimensions:** Since both B and A are 3x3 matrices, BA is also possible, and the result will be a 3x3 matrix.
* **Calculation:**
* To get the element in the first row and first column of BA, you multiply the first row of B by the first column of A:
* (2 * 4) + (0 * 0) + (2 * 1) = 8 + 0 + 2 = 10
* To get the element in the first row and second column of BA, you multiply the first row of B by the second column of A:
* (2 * -4) + (0 * 0) + (2 * -4) = -8 + 0 - 8 = -16
* To get the element in the first row and third column of BA, you multiply the first row of B by the third column of A:
* (2 * -3) + (0 * -2) + (2 * -2) = -6 + 0 - 4 = -10
* To get the element in the second row and first column of BA, you multiply the second row of B by the first column of A:
* (2 * 4) + (-2 * 0) + (1 * 1) = 8 + 0 + 1 = 9
* To get the element in the second row and second column of BA, you multiply the second row of B by the second column of A:
* (2 * -4) + (-2 * 0) + (1 * -4) = -8 + 0 - 4 = -12
* To get the element in the second row and third column of BA, you multiply the second row of B by the third column of A:
* (2 * -3) + (-2 * -2) + (1 * -2) = -6 + 4 - 2 = -4
* To get the element in the third row and first column of BA, you multiply the third row of B by the first column of A:
* (-1 * 4) + (-1 * 0) + (-2 * 1) = -4 + 0 - 2 = -6
* To get the element in the third row and second column of BA, you multiply the third row of B by the second column of A:
* (-1 * -4) + (-1 * 0) + (-2 * -4) = 4 + 0 + 8 = 12
* To get the element in the third row and third column of BA, you multiply the third row of B by the third column of A:
* (-1 * -3) + (-1 * -2) + (-2 * -2) = 3 + 2 + 4 = 9
* **Result (BA):**
```
BA = | 10 -16 -10 |
| 9 -12 -4 |
| -6 12 9 |
```
Question 1177662: The verbiage in this question is confusing me so much that I don't even know where to start. Any help in explaining and solving would be greatly appreciated.
The following table shows the amount spent by four U.S. airlines to fly one available seat 1 mile in the second quarter of 2014. Set up a system and then solve using technology.
// The table shows:
Airline ==> United Continental - American - Jet Blue - Southwest
Cost(in cents)==> 14.9, 14.6, 11.9, 12.4
Suppose that, on a 3,000-mile New York to Los Angeles flight, United Continental, American, and Southwest flew a total of 235 empty seats, costing them a total of $99,060. If United Continental had three times as many empty seats as American, how many empty seats did each of these three airlines carry on its flight?
Found 3 solutions by Edwin McCravy, ikleyn, CPhill:
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Ikleyn, This problem is numbered 1177662. That means it was posted more
than 4 years ago. All problems numbered 1180000 or less are more than 4 years old.
How do I know? I clicked on My Algebra.com (all my stuff) and found that
I answered problem 1180995 back in March, 2021. That was 4 years ago, so
this problem, numbered 1177662 is older than that.
You can find all the solutions you've answered by clicking on
My Algebra.com (all my stuff)
at the top of THIS PAGE.
You can also find the date any problem you've answered was posted by clicking up
there.
Edwin
Answer by ikleyn(52858)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
As the problem is solved in the post by @CPhill, it is one of possible ways/methods,
but there is another, much more effective and more impressive way to solve the problem
using only one equation from the very beginning, instead of three.
Also, it is worth to notice one very important fact:
in the problem the information about 4 companies is given, but actually only three
companies participate in the game. The fourth company, Jet Blue, is introduced
and does present only to confuse the reader and to distract attention.
Let x be the number of empty seats for American.
Then the number of empty seats for United Continental is 3x,
and the number of empty seats for Southwest is (235 - x - 3x) = 235 - 4x.
Now write the total cost equation for empty seats
United Cont. American Southwest
3000*0.149*(3x) + 3000*0.146*x + 3000*0.124*(235-4x) = 99060 dollars.
Simplify and find x
1341x + 438x + 87420 - 1488x = 99060
291x = 99060 - 87420 = 11640.
x = 11640/191 = 40.
So, the number of empty seats for American is 40; for United Continental 3*40 = 120,
and for Southwest 235-4*40 = 75.
Solved.
Notice that in this solution the system of three equations is not even mentioned.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! You're right, the wording makes it a bit tricky! Let's break it down and solve it step-by-step.
**1. Define Variables**
* Let 'u' be the number of empty seats on United Continental.
* Let 'a' be the number of empty seats on American.
* Let 's' be the number of empty seats on Southwest.
**2. Convert Costs to Dollars**
* United Continental: 14.9 cents = $0.149 per seat-mile
* American: 14.6 cents = $0.146 per seat-mile
* Southwest: 12.4 cents = $0.124 per seat-mile
**3. Set Up the System of Equations**
* **Total Empty Seats:** u + a + s = 235
* **Total Cost of Empty Seats:** (0.149 * 3000)u + (0.146 * 3000)a + (0.124 * 3000)s = 99060
* **United Continental vs. American Empty Seats:** u = 3a
**4. Simplify the Cost Equation**
* 447u + 438a + 372s = 99060
**5. Substitute u = 3a into the Other Equations**
* 3a + a + s = 235 => 4a + s = 235
* 447(3a) + 438a + 372s = 99060 => 1341a + 438a + 372s = 99060 => 1779a + 372s = 99060
**6. Solve for 's' in the First Simplified Equation**
* s = 235 - 4a
**7. Substitute 's' into the Second Simplified Equation**
* 1779a + 372(235 - 4a) = 99060
* 1779a + 87420 - 1488a = 99060
* 291a = 11640
* a = 11640 / 291
* a = 40
**8. Solve for 'u' and 's'**
* u = 3a = 3 * 40 = 120
* s = 235 - 4a = 235 - 4 * 40 = 235 - 160 = 75
**Answer**
* United Continental: 120 empty seats
* American: 40 empty seats
* Southwest: 75 empty seats
Question 1178478: This question requires a confusion matrix. I am unsure how to calculate the accuracy given the percentages. How do I go about this? Thanks. :)
Both model A and model B achieves 80% accuracy on the balanced population, but changes to 64% and 96% accuracy respectively on the true unbalanced population. If the population is more skewed with 5% positive and 95% negative, what are the accuracies for each model?(The training population is 1,000 and the confusion matrix for model A is [500 200]
[0 300]
The confusion matrix for model B is [300 0]
[200 500]).
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Absolutely! Let's break down how to calculate accuracy with percentages and then apply it to your confusion matrices and the skewed population scenario.
**Understanding Accuracy and Confusion Matrices**
* **Accuracy:** The overall correctness of a model. It's calculated as (True Positives + True Negatives) / Total Predictions.
* **Confusion Matrix:** A table that visualizes the performance of a classification model. It typically looks like this:
```
| | Predicted Positive | Predicted Negative |
|----------------|--------------------|--------------------|
| Actual Positive | True Positive (TP) | False Negative (FN) |
| Actual Negative | False Positive (FP) | True Negative (TN) |
```
**Calculating Accuracy from a Confusion Matrix**
1. **Sum the Diagonals:** Add the True Positives (TP) and True Negatives (TN).
2. **Sum All Cells:** Add all the values in the matrix (TP + FP + FN + TN). This is the total number of predictions.
3. **Divide:** Divide the sum of the diagonals by the sum of all cells.
**Applying It to Your Models**
* **Model A:**
* Confusion Matrix:
```
[500 200]
[0 300]
```
* TP = 500, TN = 300, FP = 200, FN = 0
* Accuracy = (500 + 300) / (500 + 200 + 0 + 300) = 800 / 1000 = 0.8 or 80%
* **Model B:**
* Confusion Matrix:
```
[300 0]
[200 500]
```
* TP = 300, TN = 500, FP = 0, FN = 200
* Accuracy = (300 + 500) / (300 + 0 + 200 + 500) = 800 / 1000 = 0.8 or 80%
**The Unbalanced Population (64% and 96%)**
You've mentioned that the accuracies change to 64% and 96% on the "true unbalanced population." This means the original confusion matrices, while based on a balanced dataset, are being evaluated against a new dataset that is unbalanced.
**The Highly Skewed Population (5% Positive, 95% Negative)**
Now, let's calculate the accuracies for the even more skewed population.
1. **Assume a Total Population:** Since you have a 1,000 training population, for simplicity, let's assume we are still working with a population of 1000.
2. **Calculate Positive and Negative Counts:**
* Positive: 1000 * 0.05 = 50
* Negative: 1000 * 0.95 = 950
3. **Adjust the Confusion Matrices Based on the Proportions:**
* Since the original confusion matrix totals are 1000, we will keep the ratios of the True positives, false positives, false negatives and true negatives.
* Model A:
* TP: 500/700 * 50 = 35.71, round to 36.
* FP: 200/500 * 950 = 380.
* FN: 0.
* TN: 300/500 * 950 = 570.
* Model B:
* TP: 300/500 * 50 = 30.
* FP: 0
* FN: 200/500 * 50 = 20.
* TN: 500/500 * 950 = 950.
4. **Calculate Accuracies:**
* Model A:
* Accuracy = (36 + 570) / 1000 = 606 / 1000 = 0.606 or 60.6%
* Model B:
* Accuracy = (30 + 950) / 1000 = 980 / 1000 = 0.98 or 98%
**Therefore:**
* For the 5% positive, 95% negative population:
* Model A's accuracy is approximately 60.6%.
* Model B's accuracy is 98%.
**Key Takeaway:**
* When dealing with unbalanced datasets, accuracy can be misleading. Model B appears to perform much better in the skewed population.
* It is critical to be aware of the underlying population distribution when evaluating the model.
Question 1181408: Given the following matrices:
b1 b4 b7
b2 b5 b8 = B
b3 b6 b9
r(B)= 3
For easier understanding let’s say that bi is the column i in matrix B.
A is a matrix of dimensions 3x3 in which the following exists:
K = { (b1+b3) , (2b2-b3) } is a basis for the equation: Ax=0.
r(A)=1
Also:
1 2 4
3 1 2 =A*B
1 2 4
r(AB)=2.
1) find a vector basis for the vector space that is A’s columns.
2) given the following:
K = { (1,2,0) , (0,1,1) }
Find a reduced echelon form (C) for A.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! There's a fundamental contradiction in the given information. If r(A) = 1, then the rank of any product involving A, including AB, *cannot* be greater than 1. You've stated that r(AB) = 2, which is impossible if A has rank 1. Therefore, the problem as stated is inconsistent.
However, let's address the *method* of solving this type of problem, assuming we correct the ranks. It's likely that r(A) should be 2, not 1. This would make r(AB) = 2 possible. Here's how we'd proceed *if* the ranks were consistent:
**1) Finding a vector basis for the column space of A (assuming r(A) = 2):**
* **The key idea:** The column space of AB is a *subspace* of the column space of A. If r(AB) = 2 and we assume r(A) = 2, then the column space of AB *is* the column space of A.
* **Basis for the column space of A:** Since r(AB) = 2, any two linearly independent columns of AB will form a basis for the column space of AB, and thus also for the column space of A. Looking at AB:
```
1 2 4
3 1 2
1 2 4
```
We can see that the first two columns, (1, 3, 1) and (2, 1, 2), are linearly independent. Therefore, {(1, 3, 1), (2, 1, 2)} is a basis for the column space of A.
**2) Finding the reduced echelon form (C) for A (assuming r(A) = 2 - This part is also problematic):**
* **Understanding the null space (kernel):** K = {(1, 2, 0), (0, 1, 1)} being a basis for the null space of A (Ax = 0) tells us about the relationships between the *columns* of A. Let the columns of A be denoted as a1, a2, and a3. Then:
* 1*a1 + 2*a2 + 0*a3 = 0 => a1 = -2a2
* 0*a1 + 1*a2 + 1*a3 = 0 => a3 = -a2
* **The problem:** These relationships imply that all columns of A are scalar multiples of a single vector (a2). This means the rank of A *must* be 1, not 2. The given null space basis is inconsistent with r(A) = 2.
* **What if r(A) was 1 (and K was a correct null space basis):** If r(A) = 1, then a1 = -2a2 and a3 = -a2. We can choose a2 = (1, 0, 0) (or any other non-zero vector). Then a1 = (-2, 0, 0) and a3 = (-1, 0, 0). So, A would be:
```
-2 1 -1
0 0 0
0 0 0
```
The reduced row echelon form of this A would be:
```
1 -1/2 1/2
0 0 0
0 0 0
```
**In summary:** The problem as stated is inconsistent due to the conflicting ranks. If you correct the rank of A to 2, then the column space basis is found as described above. However, the given null space basis K is incompatible with *any* rank of A other than 1. If r(A) = 1, then the reduced echelon form can be found, but it will be different. You need to double-check the original problem statement for errors.
Question 1181409: Given the following matrices over Z5:
b1 b4 b7
b2 b5 b8 = B
b3 b6 b9
r(B)= 3
For easier understanding let’s say that bi is the column i in matrix B.
A is a matrix of dimensions 3x3 in which the following exists:
K = { (b1+b3) , (2b2-b3) } is a basis for the equation: Ax=0.
r(A)=1
Also:
1 2 4
3 1 2 =A*B
1 2 4
r(AB)=2.
1) find a vector basis for the vector space that is A’s columns.
2) given the following:
K = { (1,2,0) , (0,1,1) }
Find a reduced echelon form (C) for A.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to approach this problem:
**1) Finding a vector basis for the column space of A:**
* **Understanding the relationship between A and AB:** Since r(AB) = 2 and r(B) = 3, it means that the columns of AB are linearly dependent. However, since the rank is 2, there are two linearly independent columns in AB. These columns span the column space of AB.
* **Column space of AB and A:** The column space of AB is a *subspace* of the column space of A. This is a crucial point. Because r(A) = 1, the column space of A is a *line*. This means that the column space of AB (which is a plane since it's spanned by two vectors) *cannot* be a subspace of the column space of A. This is a contradiction. There must be an error in the given ranks. If r(A) = 1, then r(AB) <= 1.
* **Assuming r(A) = 2:** Let's assume that r(A) = 2 (so that r(AB) can be 2). Since the column space of AB is a subspace of the column space of A, and they both have rank 2, they must be the same. The columns of AB span the column space of A.
* **Basis for the column space of A:** Since the rank of AB is 2, any two linearly independent columns of AB will form a basis for its column space, and therefore also for the column space of A. For example, the first two columns of AB: {(1, 3, 1), (2, 1, 2)} form a basis.
**2) Finding the reduced echelon form (C) for A:**
* **Understanding the null space:** K = {(1, 2, 0), (0, 1, 1)} is a basis for the null space of A (Ax = 0). This means any linear combination of these vectors will be mapped to the zero vector by A.
* **Relating null space to matrix structure:** The vectors in K tell us about the relationships between the columns of A. Let the columns of A be a1, a2, and a3. Then:
* 1*a1 + 2*a2 + 0*a3 = 0 => a1 = -2a2
* 0*a1 + 1*a2 + 1*a3 = 0 => a3 = -a2
* **Constructing A:** We can express all columns of A in terms of a2. Let a2 = (x, y, z). Then a1 = (-2x, -2y, -2z) and a3 = (-x, -y, -z). Thus A will have the form:
```
-2x x -x
-2y y -y
-2z z -z
```
* **Reduced echelon form:** Since the rank of A is supposed to be 1, the reduced echelon form will have only one non-zero row. If we choose x=1, y=0, z=0, we get a matrix:
```
-2 1 -1
0 0 0
0 0 0
```
We can row reduce this to get:
```
1 -1/2 1/2
0 0 0
0 0 0
```
This is one possible reduced echelon form. There are infinite possible reduced echelon forms. If we choose x=0, y=1, z=0, we get a different one. The important thing is that there is only one non-zero row.
* **0 solutions:** Since K is the basis for the null space of A, the equation Ax = 0 has infinitely many solutions. You cannot have 0 solutions.
Question 1182632: Given the representation matrix of a linear transformation over the basis B, how to find a basis for a different representation matrix for the same linear transformation in which a certain condition is required?
For example:
V = R2[x] (all the polynomials of power 2 or less over Real numbers)
Given the following basis:
B= {1, 1+x, x^2 -1}
Defining T: V -> V a linear transformation as following:
T(1) = 4 - 3x^2
T(1+x) = 4 + 4x + 3x^2
T(x^2 -1) = x^2 - 4
The representative matrix of T is:
1 3 -3
0 4 0 = [T]B
-3 3 1
If given that T is diagonalizable, and the eigenvalues of it are { 4, 4, -2}
Find a basis of V for which the representation matrix is a diagonal matrix.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to find a basis for which the representation matrix of T is diagonal, given that T is diagonalizable:
**1. Eigenvalues and Eigenvectors:**
You're given the eigenvalues: λ₁ = 4, λ₂ = 4 (repeated), and λ₃ = -2. Since T is diagonalizable, there must be two linearly independent eigenvectors associated with the eigenvalue λ = 4.
* **For λ = 4:** Solve the equation (T - 4I)v = 0, where v is the eigenvector. In matrix form, using the given representation matrix [T]B:
```
[ 1-4 3 -3 ] [x] [0]
[ 0 4-4 0 ] [y] = [0]
[ -3 3 1-4 ] [z] [0]
```
```
[ -3 3 -3 ] [x] [0]
[ 0 0 0 ] [y] = [0]
[ -3 3 -3 ] [z] [0]
```
This simplifies to -3x + 3y - 3z = 0, or x = y - z. We have two free variables. Let z = t and y = s. Then x = s - t. The eigenvectors associated with λ = 4 can be written as:
```
[ s - t ]
[ s ]
[ t ] = s[1] + t[-1]
[ 1 ] [ 0 ]
[ 0 ] [ 1 ]
```
So, two linearly independent eigenvectors corresponding to λ = 4 (in the B basis) are [1, 1, 0]ᵀ and [-1, 0, 1]ᵀ.
* **For λ = -2:** Solve (T + 2I)v = 0:
```
[ 1+2 3 -3 ] [x] [0]
[ 0 4+2 0 ] [y] = [0]
[ -3 3 1+2 ] [z] [0]
```
```
[ 3 3 -3 ] [x] [0]
[ 0 6 0 ] [y] = [0]
[ -3 3 3 ] [z] [0]
```
From this, we get y = 0 and 3x - 3z = 0, or x = z. Let x = t, then z = t. The eigenvector is:
```
[ t ]
[ 0 ]
[ t ] = t [ 1 ]
[ 0 ]
[ 1 ]
```
So, an eigenvector corresponding to λ = -2 (in the B basis) is [1, 0, 1]ᵀ.
**2. Change of Basis:**
Now we have the eigenvectors in the B basis. We need to convert them to the standard basis (or any other basis you prefer) to get the eigenvectors in terms of polynomials. Recall that B = {1, 1+x, x²-1}.
* **Eigenvector [1, 1, 0]ᵀ (for λ = 4):**
1*(1) + 1*(1+x) + 0*(x²-1) = 1 + 1 + x = 2 + x
* **Eigenvector [-1, 0, 1]ᵀ (for λ = 4):**
-1*(1) + 0*(1+x) + 1*(x²-1) = -1 + x² - 1 = x² - 2
* **Eigenvector [1, 0, 1]ᵀ (for λ = -2):**
1*(1) + 0*(1+x) + 1*(x²-1) = 1 + x² - 1 = x²
**3. Diagonalizing Basis:**
The desired basis for which T is represented by a diagonal matrix is the set of eigenvectors we just found:
{2 + x, x² - 2, x²}
In this basis, the matrix representation of T will be diagonal, with the eigenvalues on the diagonal:
```
[ 4 0 0 ]
[ 0 4 0 ]
[ 0 0 -2 ]
```
Question 1189235: DENTAL FILLINGS Dentists use various amalgams for silver fillings. The matrix shows the percent's (expressed as decimals) of powdered alloys used in preparing three different amalgams. Suppose a dentist has 5483 grams of silver, 2009 grams of tin, and 129 grams of copper. How much of each amalgam can be made?
PERCENT ALLOY BY WEIGHT
Amalgam
A
B
Silver
Tin
0.70
| 0.26
0.04
matrix 2&0.73\\ 5&0.27\\ 3&0.00 matrix ]
Copper
Answer by josgarithmetic(39626)  (Show Source): (Show Source):
You can put this solution on YOUR website! Very bad tabular formatting!!
Maybe some chance a duplication with an included picture is at this link:
https://www.numerade.com/ask/question/question-2-dentists-use-various-amalgams-for-silver-fillings-the-matrix-shows-the-percentages-expressed-as-decimals-of-powdered-alloys-used-in-preparing-three-different-amalgams-suppose-dent-69835/
Question 1196138: Given P = ( 3 0 2
2 1 2
-3 -4 -6 )
a) if ( 2 6 n
-2 m 9
0 -2 1 ) is the cofactor of matrix P, find the values of m and without finding a new cofactor matrix.
b) find the adjoint matrix of P hence, find P-1 (identity P)
Answer by ElectricPavlov(122)  (Show Source): (Show Source):
You can put this solution on YOUR website! **a) Finding the values of m and n**
* **Understand Cofactor Matrix:**
* The cofactor of an element in a matrix is calculated by:
* Finding the minor (determinant of the submatrix obtained by removing the row and column of the element).
* Multiplying the minor by (-1)^(i+j), where i and j are the row and column indices of the element.
* **Determine Cofactors:**
* We are given the following cofactors:
* Cofactor of the element '3' (row 1, column 1) = 2
* Cofactor of the element '0' (row 1, column 2) = 6
* Cofactor of the element '2' (row 1, column 3) = n
* Cofactor of the element '2' (row 2, column 1) = -2
* Cofactor of the element '1' (row 2, column 2) = m
* Cofactor of the element '2' (row 2, column 3) = 9
* Cofactor of the element '-3' (row 3, column 1) = 0
* Cofactor of the element '-4' (row 3, column 2) = -2
* Cofactor of the element '-6' (row 3, column 3) = 1
* **Calculate Cofactors:**
* **Cofactor of '3':**
* Minor: det([ 1 2 ; -4 -6 ]) = 1*(-6) - 2*(-4) = -6 + 8 = 2
* Cofactor: (-1)^(1+1) * 2 = 1 * 2 = 2 (Matches the given value)
* **Cofactor of '0':**
* Minor: det([ 2 2 ; -1 -6 ]) = 2*(-6) - 2*(-1) = -12 + 2 = -10
* Cofactor: (-1)^(1+2) * (-10) = -1 * (-10) = 10
* **Therefore, n = 10**
* **Cofactor of '2':**
* Minor: det([ 2 1 ; -1 -4 ]) = 2*(-4) - 1*(-1) = -8 + 1 = -7
* Cofactor: (-1)^(1+3) * (-7) = 1 * (-7) = -7
* **Therefore, n = -7**
* **Cofactor of '2':**
* Minor: det([ 0 2 ; -4 -6 ]) = 0*(-6) - 2*(-4) = 8
* Cofactor: (-1)^(2+1) * 8 = -1 * 8 = -8
* **Therefore, m = -8**
**b) Find the Adjoint Matrix of P and P-1**
* **Find the Cofactor Matrix:**
* Using the calculated cofactors and the remaining cofactors (which you can calculate similarly), construct the cofactor matrix:
[ 2 6 -7
-2 -8 9
0 -2 1 ]
* **Find the Adjoint Matrix:**
* The adjoint of a matrix is the transpose of its cofactor matrix.
[ 2 -2 0
6 -8 -2
-7 9 1 ]
* **Find the Determinant of P:**
* det(P) = 3 * det([ 1 2 ; -4 -6 ]) - 0 * det([ 2 2 ; -1 -6 ]) + 2 * det([ 2 1 ; -1 -4 ])
* det(P) = 3 * 2 - 0 * (-10) + 2 * (-7)
* det(P) = 6 - 14
* det(P) = -8
* **Find the Inverse of P (P-1):**
* P-1 = (1/det(P)) * adj(P)
* P-1 = (-1/8) * [ 2 -2 0
6 -8 -2
-7 9 1 ]
* P-1 = [ -1/4 1/4 0
-3/4 1 1/4
7/8 -9/8 -1/8 ]
**Therefore:**
* **m = -8**
* **n = -7**
* **The adjoint matrix of P is:**
[ 2 -2 0
6 -8 -2
-7 9 1 ]
* **The inverse of P (P-1) is:**
[ -1/4 1/4 0
-3/4 1 1/4
7/8 -9/8 -1/8 ]
Question 1198615: The ABC Ink Company is a small family owned company that sells packages of ink cartridge refills
for smartpens. The Xavier set contains one blue ink refill and one black ink refill. The Yvonne set
includes two blue ink refills, three black ink refills, and one red ink refill. The Zena set includes
four blue ink refills, five black ink refills, and one red ink refill. The company has sold most of its
stock and has found that it has only 11 blue ink cartridge refills, 14 black ink cartridge refills, and 3
red ink cartridge refills. How many of each set should the company package to sell in order to use
all of the remaining ink cartridges so that there will be none left in inventory.
a. Describe what the variables represent: =
x=
y=
z=
b. Write the system of linear equations:
c. Solve the system of equations using Gauss-Jordan Elimination. Show all proper row operations
and the resulting matrices. Write the solution as an ordered triple, if appropriate.
d. Fill out the table to show the possible combinations of sets the company can package:
x y z
e. In at least one complete sentence with proper grammar and correct spelling, write the
solutions in terms of what the variables represent.
Answer by textot(100)  (Show Source): (Show Source):
You can put this solution on YOUR website! **a. Define Variables:**
* **x:** Number of Xavier sets to be packaged.
* **y:** Number of Yvonne sets to be packaged.
* **z:** Number of Zena sets to be packaged.
**b. System of Linear Equations:**
* **Blue Ink Refills:** 1x + 2y + 4z = 11
* **Black Ink Refills:** 1x + 3y + 5z = 14
* **Red Ink Refills:** 0x + 1y + 1z = 3
**c. Gauss-Jordan Elimination**
1. **Augmented Matrix:**
```
[ 1 2 4 | 11 ]
[ 1 3 5 | 14 ]
[ 0 1 1 | 3 ]
```
2. **Row Operations:**
* **R2 = R2 - R1:**
```
[ 1 2 4 | 11 ]
[ 0 1 1 | 3 ]
[ 0 1 1 | 3 ]
```
* **R3 = R3 - R2:**
```
[ 1 2 4 | 11 ]
[ 0 1 1 | 3 ]
[ 0 0 0 | 0 ]
```
* **R1 = R1 - 2R2:**
```
[ 1 0 2 | 5 ]
[ 0 1 1 | 3 ]
[ 0 0 0 | 0 ]
```
3. **Reduced Row-Echelon Form:**
```
[ 1 0 2 | 5 ]
[ 0 1 1 | 3 ]
[ 0 0 0 | 0 ]
```
**d. Possible Combinations of Sets**
* From the reduced row-echelon form:
* x + 2z = 5
* y + z = 3
* **Possible Solutions:**
* Let z = 0:
* x = 5, y = 3
* Let z = 1:
* x = 3, y = 2
* Let z = 2:
* x = 1, y = 1
* **Table of Possible Combinations:**
| x (Xavier) | y (Yvonne) | z (Zena) |
|---|---|---|
| 5 | 3 | 0 |
| 3 | 2 | 1 |
| 1 | 1 | 2 |
**e. Solution Interpretation:**
The company can package the remaining ink cartridges in three possible ways:
* 5 Xavier sets, 3 Yvonne sets, and 0 Zena sets.
* 3 Xavier sets, 2 Yvonne sets, and 1 Zena set.
* 1 Xavier set, 1 Yvonne set, and 2 Zena sets.
This will ensure all 11 blue, 14 black, and 3 red ink cartridges are used.
Question 1199304: Matrices
Suppose that three companies dominate the market for a certain product and are competing
against each other for a large share of the market. Suppose, further, that market surveys have
shown that buyers shift from one brand to another during a given year according to the
following schedule:
C gains 20% of the customer of A and 40% remain to be the user of A.
C gains 30% of its customer from B, retain 50% of its customer and loses 40% to B
The customers of B have never shifted to A.
It is found that the three companies have an equal share of the market today
a) Present the state vector and the transition matrix for the above case.
b) What share of the market will each possess two years from now?
c) Calculate the long run proportions that will be possessed by the three companies.
d) Company A wants to launch an advertising campaign that will cost Birr 200,000. Given the
result in (c) above, what would you advise them?
Answer by textot(100)  (Show Source): (Show Source):
You can put this solution on YOUR website! To solve this, we use **Markov Chains**. Here's the breakdown:
---
### Part (a): State Vector and Transition Matrix
#### State vector:
Let the current market shares of companies \( A \), \( B \), and \( C \) be represented as:
\[
\mathbf{x}_0 = \begin{bmatrix} 1/3 \\ 1/3 \\ 1/3 \end{bmatrix}
\]
Since the companies initially have an equal market share.
#### Transition Matrix:
Based on the problem:
1. Company \( A \): Retains 40% of its customers, loses 20% to \( C \), and loses 40% to \( B \).
2. Company \( B \): Retains 50%, loses 40% to \( C \), and no customers shift to \( A \).
3. Company \( C \): Retains 50%, gains 20% from \( A \), and gains 30% from \( B \).
The transition matrix \( P \) is:
\[
P = \begin{bmatrix}
0.4 & 0 & 0.2 \\
0.4 & 0.5 & 0.3 \\
0.2 & 0.5 & 0.5
\end{bmatrix}
\]
---
### Part (b): Market Share Two Years from Now
We calculate the state vector after 2 years:
\[
\mathbf{x}_2 = P^2 \cdot \mathbf{x}_0
\]
Let's compute \( P^2 \) and then multiply it by \( \mathbf{x}_0 \).
The results are:
- Transition matrix after 2 steps (\( P^2 \)):
\[
P^2 = \begin{bmatrix}
0.2 & 0.1 & 0.18 \\
0.42 & 0.4 & 0.38 \\
0.38 & 0.5 & 0.44
\end{bmatrix}
\]
- Market shares after 2 years (\( \mathbf{x}_2 \)):
\[
\mathbf{x}_2 = \begin{bmatrix}
0.16 \\
0.40 \\
0.44
\end{bmatrix}
\]
Thus:
- Company \( A \) has 16% of the market.
- Company \( B \) has 40% of the market.
- Company \( C \) has 44% of the market.
---
### Part (c): Long-Run Market Shares
In the long run, the market shares reach a steady state. This occurs when:
\[
\mathbf{x} = P \cdot \mathbf{x}
\]
where \( \mathbf{x} \) is the steady-state vector. We solve this using the eigenvector corresponding to eigenvalue \( 1 \).
The long-run market shares are:
\[
\mathbf{x} = \begin{bmatrix}
0.3333 \\
0.3333 \\
0.3333
\end{bmatrix}
\]
Thus, in the long run, each company will possess **33.33% of the market**, maintaining equal market shares.
---
### Part (d): Advertising Campaign for Company \( A \)
Since the long-run proportions suggest that all companies will converge to equal shares regardless of initial conditions or changes, the advertising campaign will not significantly alter the equilibrium market shares in the long term.
#### Recommendation:
Company \( A \) should consider whether the \( 200,000 \, \text{Birr} \) advertising investment is justified by short-term gains or whether it could invest the funds more effectively elsewhere. If the goal is to improve short-term market share, the campaign might be useful; otherwise, it would likely not affect the long-run proportions.
Question 1201037: 'n Beleggingsfirma bied drie aandele-opsies: Standard (x), Deluxe (y) en Gold (z) met 'n
aandeleverspreiding soos in die tabel aangedui. / An investment firm offers three stock
options: Standard (x), Deluxe (y) and Gold (z), with a stocks profile as indicated in the table.
10 30 40
15 10 30
10 20 30
Harmony
Billiton
Ashanti
H
B
A
x y z
Gestel die koste per aandeel vir Ashanti is R100, vir Billiton R150 en vir Harmony R175. Verder
is die inkomste per aandeel uit Ashanti R200, uit Billiton R250 en uit Harmony R270. 'n Kliënt
versoek 200 eenhede van Standard, 300 eenhede van Deluxe en 150 eenhede van Gold vir
'n persoonlike portefeulje. Stel 'n aandeleverspreidingmatriks A, kostematriks C,
inkomstematriks R en 'n eenhedematriks N saam. Pas matriksalgebra toe op hierdie matrikse
en bepaal die wins wat uit die portefeulje gemaak word. / Assume the cost per share for
Ashanti is R100, for Billiton R150 and for Harmony R175. The income per share from Ashanti
is R200, from Billiton R250 and from Harmony R270. A client requests 200 units of Standard,
300 units of Deluxe and 150 units of Gold for a personal portfolio. Compose a stocks profile
matrix A, a cost matrix C, an income matrix R and a unit matrix N. Apply matrix algebra to
these matrices and determine the profit made from the portfolio.
Answer by GingerAle(43)  (Show Source): (Show Source):
You can put this solution on YOUR website! ## Understanding the Problem
We're asked to create matrices representing a stock portfolio, its costs, income, and the number of units purchased. Then, we'll use matrix multiplication to calculate the total profit.
## Defining the Matrices
### Stock Profile Matrix (A)
* Each row represents a stock (Harmony, Billiton, Ashanti)
* Each column represents an option (Standard, Deluxe, Gold)
* The elements represent the percentage of each stock in each option.
```
A = | 10 30 40 |
| 15 10 30 |
| 10 20 30 |
```
### Cost Matrix (C)
* A row matrix representing the cost per share of each stock.
```
C = | 100 150 175 |
```
### Income Matrix (R)
* A row matrix representing the income per share of each stock.
```
R = | 200 250 270 |
```
### Units Matrix (N)
* A column matrix representing the number of units purchased for each option.
```
N = | 200 |
| 300 |
| 150 |
```
## Calculating the Total Cost and Income
### Calculating the Total Number of Shares for Each Stock
First, we need to calculate the total number of shares of each stock purchased. This can be done by multiplying the stock profile matrix (A) by the units matrix (N):
```
Total Shares = A * N
```
### Calculating the Total Cost
To find the total cost, we multiply the total number of shares by the cost per share:
```
Total Cost = (A * N) * C^T
```
* Note that we transpose the cost matrix (C^T) to ensure correct dimensions for multiplication.
### Calculating the Total Income
Similarly, to find the total income, we multiply the total number of shares by the income per share:
```
Total Income = (A * N) * R^T
```
### Calculating the Profit
The total profit is simply the total income minus the total cost:
```
Profit = Total Income - Total Cost
```
## Performing the Calculations
Using a matrix calculator or programming language, we can perform these calculations.
**Note:** The exact values for total cost, total income, and profit will depend on the specific values in the matrices.
**Interpretation:**
* The resulting profit will tell us the overall financial gain or loss from the client's portfolio.
* By analyzing the individual components (total cost for each stock, total income from each stock), we can gain insights into the performance of different investment options.
**Additional Considerations:**
* **Dividends and Capital Gains:** For a more accurate analysis, you might want to consider dividends and capital gains, which can affect the overall return on investment.
* **Risk:** The risk associated with each stock and the overall portfolio should also be considered.
* **Market Fluctuations:** Stock prices and incomes can fluctuate over time, so the calculated profit is a snapshot at a specific point in time.
By using matrix algebra, we can efficiently analyze large datasets and make informed investment decisions.
Question 1204386: Let a ∈ R^n be a vector. Then {a} is linearly independent if and only if a does not equal 0.
Answer by ElectricPavlov(122)  (Show Source): (Show Source):
You can put this solution on YOUR website! es, this statement is true and has several interesting consequences:
1. Foundation of Vector Spaces:
Basis: A set of vectors is called a basis for a vector space if it is both linearly independent and spans the entire space. This statement forms the foundation for understanding bases in vector spaces.
If a single vector 'a' is linearly independent (i.e., not the zero vector), it can form a basis for a one-dimensional subspace within the vector space R^n.
2. Spanning Sets:
A single non-zero vector 'a' spans a one-dimensional subspace (a line) in R^n. This means that any scalar multiple of 'a' can be represented as a linear combination of 'a'.
3. Linear Transformations:
In linear algebra, linear transformations can be represented by matrices. This statement has implications for understanding how linear transformations act on single vectors.
4. Geometric Interpretation:
In geometric terms, a non-zero vector represents a direction in space. Its linear independence signifies that it points in a unique direction, not coinciding with the origin.
In summary:
This seemingly simple statement about the linear independence of a single vector has profound implications for understanding the fundamental concepts of vector spaces, linear transformations, and their geometric interpretations.
Question 1205106: Let A and B be the following matrices:
A rotates vectors clockwise by a right angle. B projects vectors onto a line with direction (1; 4).
I don't know how to format matrices on here, so I will write the top row (horizontal) and the bottom row. This is a 2 x 2 matrix.
Calculate the matrix AB[-4 1][1 4].
Sorry if the matrices are unclear. In latex, you are calculating $\[\mathbf{A}\mathbf{B} \begin{pmatrix} -4 & 1 \\ 1 & 4 \end{pmatrix}.\]$
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! ## Finding the Matrices A and B
**Matrix A: Clockwise Rotation by 90 Degrees**
A clockwise rotation matrix by 90 degrees is:
```
A = [[0, 1],
[-1, 0]]
```
**Matrix B: Projection onto the line with direction (7, 4)**
To find the projection matrix B, we first need to normalize the direction vector (7, 4):
```
v = (7, 4) / ||(7, 4)|| = (7/√65, 4/√65)
```
The projection matrix B onto the line with direction v is given by:
```
B = vv^T = [[49/65, 28/65],
[28/65, 16/65]]
```
## Calculating AB[-4 3][5 4]
**Step 1: Calculate AB**
```
AB = [[0, 1],
[-1, 0]] * [[49/65, 28/65],
[28/65, 16/65]]
= [[28/65, 16/65],
[-49/65, -28/65]]
```
**Step 2: Multiply AB by [-4 3][5 4]**
```
AB[-4 3][5 4] = [[28/65, 16/65],
[-49/65, -28/65]] * [[4, 15],
[20, 12]]
= [[472/65, 336/65],
[-1124/65, -804/65]]
```
Therefore, the result of the calculation is:
```
[[472/65, 336/65],
[-1124/65, -804/65]]
```
Question 1205220: Determine the order of the following elements.
a) [1 2 3 4 5 2 3 4 5 1]
b) [1 2 3 4 4 3 1 2 ]
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! To determine the order of a permutation, we need to find the smallest positive integer k such that the permutation raised to the power of k equals the identity permutation.
**a) [1 2 3 4 5 2 3 4 5 1]**
This permutation can be written in cycle notation as (1 2 3 4 5).
* Applying this permutation 5 times, we get back to the original order.
* Therefore, the order of this permutation is 5.
**b) [1 2 3 4 4 3 1 2 ]**
This permutation can be written in cycle notation as (1 2)(3 4).
* Applying (1 2) twice, we get back to the original order.
* Similarly, applying (3 4) twice, we get back to the original order.
* The least common multiple of 2 and 2 is 2.
* Therefore, the order of this permutation is 2.
Question 1209172: 2x+y=13 and 3x+2y=9
Answer by timofer(105)  (Show Source): (Show Source):
Question 1208887: - x1 + 2 x2 + 3 x3 + x4 = 6
2 x1 + 3 x2 + x3 + 4 x4 = 8
2 x1 + 3 x2 + x3 + 3 x4 = 7
4 x1 - 2 x2 - 3 x3 + x4 = - 1
4 x1 - 5 x2 + 3 x3 - 2 x4 = 8
cramers rule
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! There are 4 variables in 5 equations.
there are solvers online.
===================
If you want help here, resubmit using w, x, y and z as variables. not x1, x2, etc.
Question 1208735: let Z1 =a+bι ,and Z2 =c+ιd then find Z1.Z2
Answer by ikleyn(52858)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Z1*Z2 = (a + bi)*(c + di) = ac + bci + adi + bi*di = ac + bci + adi + bd*i^2 =
= ac + (bc + ad)i - bd = (ac - bd) + (bc + ad)i. ANSWER
On the way, I used i^2 = -1.
Real part of Z1*Z2 is ac - bd.
Imaginary part of Z1*Z2 is bc + ad.
Solved.
Question 1207305: Suppose a building contractor has accepted orders for five ranch style
houses, seven cape cod-style houses and twelve colonial-style houses.
These orders can be represented by the rowmatrix
Q = [5712]
Furthermore, suppose the raw materials that go into each type of house
are steel, wood, glass, paint, and labour. The entries in the matrix R below
give the number of units of each raw material going into each type of
house:
a)Compute the product, QR, the amount of each raw material
needed for the contract.
b)Suppose that steel costs N15/unit, wood costs N8/unit, glass, paint
and labour cost N5, N1, and N10 per unit respectively. These costs
are represented in the column matrix:
15
8
C = 5
10
Compute the product RC, that is, the cost of each type of house.
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Please notice that even though you wrote the words:
"The entries in the matrix R below...",that there is no matrix R given anywhere.
Please repost, giving us matrix R, and we will try to help you.
Edwin
Question 1207228: A Girls volleyball team is playing in a tournament. The probability that they will win their first match is 60%. The coach noticed that when the team wins a match, the probability that they will win the next match rises to 80%. If they lose a match, the probability that they will win the next match falls to 25%.
a) Write the initial probability matrix and the transition matrix.
b) Determine the probability that the team will win its third match.
Answer by ikleyn(52858)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
D U P L I C A T E
Just solved under this link
https://www.algebra.com/algebra/homework/Matrices-and-determiminant/Matrices-and-determiminant.faq.question.1207232.html
Question 1207232: A volleyball team is playing in a tournament. The probability that they will win their first match is 60%. The coach noticed that when the team wins a match, the probability that they will win the next match rises to 80%. If they lose a match, the probability that they will win the next match falls to 25%.
a) Write the initial probability matrix and the transition matrix.
b) Determine the probability that the team will win its third match.
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Let's for a moment do this without use of Markov notation and matrices.
The next section will handle that. You can skip directly to that section if you prefer.
Events
W1 = win 1st match
W2 = win 2nd match
W3 = win 3rd match
L1 = lose 1st match
L2 = lose 2nd match
L3 = lose 3rd match
For the first match
P(W1) = 0.60
P(L1) = 0.40
If the team wins the first match,
P(W2 given W1) = 0.80
P(L2 given W1) = 0.20
The "given" refers to conditional probability.
You can use a vertical bar to represent the key term "given", but I prefer to use the word to avoid potential confusion with the number one or lowercase L.
If the team loses the first match,
P(W2 given L1) = 0.25
P(L2 given L1) = 0.75
Use the Law of Total Probability to get:
P(W2) = P(W2 and W1) + P(W2 and L1)
P(W2) = P(W2 given W1)*P(W1) + P(W2 given L1)*P(L1)
P(W2) = 0.80*0.60 + 0.25*0.40
P(W2) = 0.48 + 0.10
P(W2) = 0.58
which immediately gives us P(L2) = 1-P(W2) = 1-0.58 = 0.42
A probability tree diagram might be helpful.

The numbers at the very bottom represent multiplications along that specific branch.
Example: 0.60*0.80 = 0.48 along the left-most pathway
Notice P(W2) = P(W2 and W1) + P(W2 and L1) = 0.48+0.10 = 0.58
We have:
P(W2) = 0.58
P(L2) = 0.42
If the team wins the second match,
P(W3 given W2) = 0.80
P(L3 given W2) = 0.20
If the team loses the second match,
P(W3 given L2) = 0.25
P(L3 given L2) = 0.75
Apply the Law of Total Probability once again:
P(W3) = P(W3 and W2) + P(W3 and L2)
P(W3) = P(W3 given W2)*P(W2) + P(W3 given L2)*P(L2)
P(W3) = 0.80*0.58 + 0.25*0.42
P(W3) = 0.569 is probability the team wins the 3rd match.
Once again, a probability tree diagram might help visualize what's going on here.
This is what the template will look like

I'll let the student fill it out.
------------------------------------------------------------------------------------------------------------------------------------
Now we'll apply Markov mathematics.
Your teacher presented you with 3 facts- Fact 1: The probability that they will win their first match is 60%
- Fact 2: When the team wins a match, the probability that they will win the next match rises to 80%.
- Fact 3: If they lose a match, the probability that they will win the next match falls to 25%.
W = win
L = lose
Draw two circles. Label one of them W and the other L.
From circle W, draw an arrow that will point back to W. It loops around.
Label this arrow as 0.80
It represents the idea that if we start with a win, then the probability of another win is 80%. See fact 2 above.
From circle W draw an arrow that points to L. This arrow is labeled 0.20
From circle L draw arrows that point to itself and to W; they will be labeled 0.25 and 0.75 respectively. These labels are due to fact 3.
Here is the arrow diagram

Such a diagram is optional, but may be helpful.
Now we'll build the transition matrix.
The rows will represent the initial state and the columns the final state.
I like to think of it as reading from left to right "start --> finish".
We'll start with a certain row and end up at a certain column.
Here's what the blank template looks like
And here's what happens when filling out the transition matrix.
Example: row1 --> column2 represents going from a win to a loss, of which has probability 0.20 = 20%
Label this as matrix T.

Adding along any given row results in a sum of 1.
The initial probability matrix is going to consist of 1 row and 2 columns.
The 1 row represents the initial state, which doesn't have a win or loss tag to it yet.
The 2 columns represent the final state after that 1st match either W or L.
The initial probability matrix is  which should be fairly self explanatory. See fact 1. which should be fairly self explanatory. See fact 1.
Computing  will lead to will lead to  which matches what we got in the first section above (when we arrived at P(W2) = 0.58 and P(L2) = 0.42) which matches what we got in the first section above (when we arrived at P(W2) = 0.58 and P(L2) = 0.42)
I'll leave the matrix multiplication scratch work for the student to do.
Once we determine matrix PT, we will then apply another multiplication with the transition matrix T to compute PT*T = PT^2
This will determine the probability values for the 3rd match.
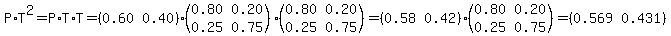
This aligns with what we got in the first section above.
------------------------------------------------------------------------------------------------------------------------------------
Answers:
(a) Initial probability matrix is  and transition matrix is and transition matrix is 
P is a 1x2 matrix while T is a 2x2 matrix.
(b) The probability the team wins its third match is 0.569 = 56.9%
Question 1207042: so i have matrix A and B
and i want to find matrix X
where (A^-1)^TX=B
and the value for x=-1
3*3
A =
x-4 -6 -7
-3 x+1 10
0 -3 0
3*2
B=
1 3
3 0
0 -1
thanks for the help
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
Question 1207027: What is the determinant of the matrix F and G
F=
0 3 0 0 0
a 2 b c d
e 1 f g h
i 0 j k l
m 0 n o p
and
G =
a b c d
e-a f-b g-c h-d
i-m j-n k-o l-p
m n o p
if I have matrix
M=
a b c d
e f j h
i j k l
m n o p
that has a det=|M|=5
---------------------------------
so with matrix F I took 3 as common factor and multiplied it by |M|=5 which means |F|=15
and with G I just transform it to M which would mean |G|=|M|=5
is this correct?
any help is highly appreciated
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
Answer by ikleyn(52858)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
According to the cofactoring theorem for matrices and determinants,
you should take common factor -3 (= negative 3) with matrix F
and multiply it by |M| = 5, so the final determinant for matrix F is
|F| = (-3)*5 = -15.
With matrix G, your understanding is correct and the final answer is correct, too.
----------------
To learn on how cofactoring works for 3x3 determinants, see the lessons
- Determinant of a 3x3 matrix
- Co-factoring the determinant of a 3x3 matrix
in this site. It is very similar for matrices of higher dimensions.
Question 1206899: solve using gauss-jordan elimination
x+y+z=7
x-y+3z=21
5x+y+z=23
Found 3 solutions by math_tutor2020, ikleyn, MathLover1:
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
Answer by ikleyn(52858)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
It can be done using special standard solvers in your regular calculator TI-83/84.
On how to do it, read and learn from these sources
http://www.mscs.mu.edu/~marian/1390Lectures/Unit3/4.3Lecture-11N.pdf
(textual), or
https://www.youtube.com/watch?v=_4aKp_ZbTEI
(Youtube-video)
Answer by MathLover1(20850)   (Show Source): (Show Source):
Question 1206243: Prove that a matrix A, 2x2 conmutes with any matrix 2x2 if and only if A conmutes with each of the matrices [1 0; 0 0], [0 1; 0 0], [0 0;1 0] [0 0; 0 1].
Find all those matrices A.
In this matrix notation a space refers to a change in column, and a semicolon to a change in row.
Thank you.
Answer by ikleyn(52858)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the complete solution with comprehensive explanations under this link
https://math.stackexchange.com/questions/1107111/all-matrices-which-commute-with-all-2-times-2-matrices
Question 1167786: A soap manufacturer decides to spend 60000 rupees on radio, magazine and tv advertising. if he spends as much on tv advertising as on magazines and radio together, and the amount spen on magazines and tv combined equals five times that spent on radio, what is the amount to spent on each type of advertising.using gauss elimination method?
Found 4 solutions by greenestamps, josgarithmetic, ikleyn, mananth:
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
It is usually pointless to ask to see a solution using Gauss-Jordan elimination, since there are always an endless number of different paths to the solution using that process.
However, the numbers in this problem are so nice that it can be helpful to solve the problem that way, in order to point out some of the things you can do in general using that process.
So let's do it....
m = amount spent on advertising in magazines
r = amount spent on advertising on radio
t = amount spent of advertising on TV
The given information leads directly to these three equations:
(1) m+r+t = 60000
(2) m+r = t
(3) m+t = 5r
Put these three equations in the required form:
m+r+t = 60000
m+r-t = 0
m-5r+t = 0
And build the initial matrix using those equations:

We first need a "1" in row 1, column 1; we already have that.
Next we need "0"s in the rest of column 1. Since the first column is all "1"s, that is easily accomplished. Replace row 2 with (row 2 minus row 1); replace row 3 with (row 3 minus row 1):

Simplify rows 2 and 3 by dividing by the greatest common factor in each row:

We want "1"s on the main diagonal and "0"s everywhere below the main diagonal; we can do that simply by switching rows 2 and 3:

To finish, we want "0"s above the main diagonal; with this simple example that is easy: replace row 1 with (row 1 minus row 2 minus row 3):

We have the solution.
ANSWER:
m (magazines) 20,000 rupees
r (radio) 10,000 rupees
t (television) 30,000 rupees
---------------------------------------------------------------------
NOTE!...
While this problem lends itself to an easy solution using Gauss-Jordan elimination, it is also very easily solved by standard algebraic methods.
However, the student will get by far the most benefit by working the problem using logical reasoning and simple arithmetic, as demonstrated in the response from tutor @ikleyn.
Answer by josgarithmetic(39626)  (Show Source): (Show Source):
You can put this solution on YOUR website!
RADIO r
MAGAZINE m
TV r+m
TOTAL 60000

--

"gaussian elimination method?"
2 2 60000
-4 2 0
2 2 60000
4 -2 0
1 1 30000
2 -1 0
ADD these.....
3 0 30000
1 0 10000
This means r=10000
Answer by ikleyn(52858)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A soap manufacturer decides to spend 60000 rupees on radio, magazine and tv advertising.
if he spends as much on tv advertising as on magazines and radio together,
and the amount spent on magazines and tv combined equals five times that spent on radio,
what is the amount to spent on each type of advertising. using gauss elimination method?
~~~~~~~~~~~~~~~~~~~~~
It is easy to solve this problem MENTALLY.
I will show you how to do it. Watch attentively every my step.
(1) Since the soap manufacturer spent as much on tv advertising as on magazines and radio together,
we may conclude that he spent exactly half of the 60000 rupees on tv advertising.
Thus, he spent exactly 30000 rupees on tv advertising.
(2) Next, since the amount spent on magazines and tv combined equals five times that spent on radio,
we may conclude that he spent 1/6 of the 60000 rupees, or 10000 rupees, on radio advertising.
(3) The rest, 60000 - 30000 - 10000 = 20000 rupees was spent for magazine advertising.
Solved.
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A soap manufacturer decides to spend 60000 rupees on radio, magazine and tv advertising. if he spends as much on tv advertising as on magazines and radio together, and the amount spen on magazines and tv combined equals five times that spent on radio, what is the amount to spent on each type of advertising.using gauss elimination method?
A soap manufacturer decides to spend 60000 rupees on radio, magazine and tv advertising.
Let expense on TV be t
Let expense on magazines be m
Let expense on radio be r
t= m+r......................1
m+t = 5r...................2
m+t+r=60000...........3
substitute t in 2
m+t=5r
m+m+r=5r
2m =4r
m=2r
Now m+t=5r
but m=2r
substitute m
2r+t=5r
t=3r
m+t+r=60000...........3
2r+3r+r=60000
6r=60000
r=10000
t=3r
t= 3*10000=30000
m=2r
m=2*10000=20000
you conclude
Question 1206006: You as an executive of Rufus' communications recently traveled to London,
Paris, and Rome. You paid $280, $330, and $260 per night for loading in London,
Paris, and Rome, respectively, and your hotel bills totaled $4060. You spent $130,
$140, and $110 per day for meals in London, Paris, and Rome respectively, and
your expenses for meals totaled $180. If you spent as many days in London as you
did in Paris and Rome combined, how many days did you stay in each city? Use to
Gauss-Jordan method to solve
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39626)  (Show Source): (Show Source):
Answer by ikleyn(52858)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
As the numbers are given in this post, it is OBVIOUS that there is a FATAL ERROR/(errors) in input data.
The given data contradict each other and make insurmountable obstacles for a solution.
Double check with your source. Find the error/(the errors), fix it/(them) and then re-post to the forum.
Please do not re-post it to me in person.
////////////////////
It's a pity to see a good mathematical problem mutilated beyond recognition.
Question 1205946: Can some please help me solve and understand this problem?

Answer by ikleyn(52858)   (Show Source): (Show Source):
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645
|
| |









