Question 1179222: At a local Brownsville play production, 420 tickets were sold. The ticket prices varied on the seating arrangements and cost $8, $10, or $12. The total income from ticket sales reached $3920. If the combined number of $8 and $10 priced tickets sold was 5 times the number of $12 tickets sold, how many tickets of each type were sold?
Found 3 solutions by josgarithmetic, MathLover1, ikleyn:
Answer by josgarithmetic(39621)   (Show Source): (Show Source):
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
At a local Brownsville play production,  tickets were sold. tickets were sold.
let's ticket that cost $ be be  , ticket that cost $ , ticket that cost $ be be  , and ticket that cost $ , and ticket that cost $ be be 
 .........eq.1 .........eq.1
if the total income from ticket sales reached $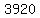 , we have , we have
 .....eq.2 .....eq.2
If the combined number of $ and $ and $ priced tickets sold was 5 times the number of $ priced tickets sold was 5 times the number of $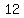 tickets, we have tickets, we have
 ....eq.3 ....eq.3
go to
 .........eq.1, substitute .........eq.1, substitute 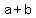 from eq.3 from eq.3




go to
 ....eq.3 ....eq.3
 ..........solve for ..........solve for 
 ..............eq.1) ..............eq.1)
go to
 .....eq.2, substitute .....eq.2, substitute  and and 
 .......solve for .......solve for 





go to
 ..............eq.1), substitute ..............eq.1), substitute 


sold, how many tickets of each type were sold?
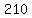 tickets that cost $ tickets that cost $ were sold, were sold,
 tickets that cost $ tickets that cost $ were sold, were sold,
and  tickets that cost $ tickets that cost $ were sold were sold
Answer by ikleyn(52824)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
At a local Brownsville play production, 420 tickets were sold.
The ticket prices varied on the seating arrangements and cost $8, $10, or $12.
The total income from ticket sales reached $3920.
If the combined number of $8 and $10 priced tickets sold was 5 times the number of $12 tickets sold,
how many tickets of each type were sold?
~~~~~~~~~~~~
Let x be the number of the $8 tickets, and
let y be the number of the $10 tickets.
Then, from the condition, the number (x+y) is 5/6 of 420, i.e. x+y = 350,
and the number of those who bought the $12 tickets was the rest 1/6 of 420, i.e. 70 persons.
Now we have the system of 2 (two) equations in two unknowns
x + y = 350 (1)
8x + 10y + 12*70 = 3920 (2) (total revenue)
We simplify this system to this EQUIVALENT strandard form
x + y = 350 (3)
8x + 10y = 3080 (4)
Multiply equation (3) by 10 (both sides) and then subtract from it equation (4). You will get then
10x - 8x = 3500 - 3080
2x = 420
x = 420/2 = 210.
Thus 210 persons bought $8 tickets; hence, 350-210 = 140 bought $10 tickets; and the rest 70 persons bought $12 tickets.
Solved.
////////////
By the way, the problem' setup, presented in the post by @josgarithmetic,
IS TOTALLY WRONG,
so for your safety, you better ignore it . . .
|
|
|