SOLUTION: Bob and Moe set off at the same time on a 30 km walk for charity. Bob walks 1.4 km/h faster than Moe, but stops for 20 min on route. Even with the delay, Bob finishes 2 hours ahead

Algebra ->  Coordinate Systems and Linear Equations  -> Linear Equations and Systems Word Problems -> SOLUTION: Bob and Moe set off at the same time on a 30 km walk for charity. Bob walks 1.4 km/h faster than Moe, but stops for 20 min on route. Even with the delay, Bob finishes 2 hours ahead      Log On


   

Question 1163722: Bob and Moe set off at the same time on a 30 km walk for charity. Bob walks 1.4 km/h faster than Moe, but stops for 20 min on route. Even with the delay, Bob finishes 2 hours ahead of Moe. How fast in km/h was Bob walking, and how long in hours did it take for Moe to finish the walk?
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52786) About Me  (Show Source):
You can put this solution on YOUR website!
.
Bob and Moe set off at the same time on a 30 km walk for charity. Bob walks 1.4 km/h faster than Moe, but stops for 20 min on route.
Even with the delay, Bob finishes 2 hours ahead of Moe.
How fast in km/h was Bob walking, and how long in hours did it take for Moe to finish the walk?
~~~~~~~~~~~~~~ 


Let x be the Bob's rate, in km/h (the value under the problem's question).

Then Moe's rate is (x-1.4) km/h, according to the condition.


Bob's time walking is 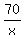 70%2Fx  hours  (with no counting the time for stop).

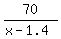Moe's time walking is  70%2F%28x-1.4%29  hours.


The time equation for their trips is

    Moe's time - Bob's time = 2 hours,


Or in the Math form,

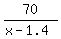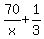    70%2F%28x-1.4%29 - ( 70%2Fx+%2B+1%2F3 ) = 2.


Here 1%2F3 represets Bob's 20 minute stop.


So, your final setup "time equation" is

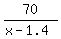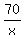    70%2F%28x-1.4%29 - 70%2Fx = 7%2F3.


7%2F3 in the right side is  2 + 1%2F3.


I will leave the solution of this equation to you, because the rest is just a technique.


Your next steps are 

    1)  multiply both sides by 3x*(x-1.4);  

    2)  then reduce it to the standard quadratic equation

    3)  then solve it via the quadratic formula or factoring (whichever methods works and whichever you prefer).

At this point, I complete my instructions.

The rest is on you.

-------------

To see many other similar solved problems amd/or to learn more about time equation,  look into the lessons
    - Had a car move faster it would arrive sooner
    - How far do you live from school?
    - Earthquake waves
    - Time equation: HOW TO use, HOW TO write and HOW TO solve it
in this site.

==================================

If you will have difficulties or questions, do not hesitate ask me.

If you do, then please refer to the ID number of this problem, which is 1163722.

The ID number is the first number, which you see in your page in the UPPER LEFT corner.

If you will post to me without referring to this ID number, I will not know to whom to answer.

It is how this forum works.

So, mentioning this ID is NECESSARY, if you want to have two-way communication with me.


Good luck (!)



Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
Bob and Moe set off at the same time on a 30 km walk for charity.
Bob walks 1.4 km/h faster than Moe,
Let Moe's rate be r
Then Bob's rate is r+1.4

Make this chart:

                  Distance       Rate      Time
Moe on the 30 km     30           r       30/r
------------------------------------------------------
Bob on the 30 km     30         r+1.4   30/(r+1.4)

but [Bob] stops for 20 min on route. 
That's 1/3 of an hr.
                                      
                 Distance      Rate      Time
Moe                30           r       30/r
------------------------------------------------------
Bob on the 30 km   30         r+1.4   30/(r+1.4) 
Bob's stop          0           0       1/3 h  
--------------------------------------------------------

Even with the delay, Bob finishes 2 hours ahead of Moe.
%28matrix%283%2C1%2C%22Bob%27s%22%2C%22total%22%2C%22time%22%29%29%22%22=%22%22%28matrix%283%2C1%2C%22Moe%27s%22%2C+total%2C+time%29%29%22%22-%22%222     

30%2F%28r%2B1.4%29%2B1%2F3%22%22=%22%2230%2Fr-2

90r%2Br%28r%2B1.4%29+=+90%28r%2B1.4%29-6r%28r%2B1.4%29

Solve that (you can use the quadratic formula if you
can't factor.

The approximate rate for Moe is about ????????? km/h

You solve the equation.

how long in hours did it take for Moe to finish the walk?
That's a trick question.  Since Bob finished 2 hours 
ahead of Moe, Moe finished 2 hours later. lol.

Hmmm.  I took it to mean how long after Bob finished did it
take for Moe to finish.   But maybe you want Moe's WHOLE
time.  If so, divide 30 by what you got for r.

Edwin