Question 1163721: A man with a scooter and two friends had to make a journey of 52 miles. The man decided he would take the first friend a certain distance while the second walked. He would drop the first friend off to walk the remainder of the 52 miles, return to meet the second friend, pick him up, and proceed to the end of the journey finishing just as the first friend finished. If the scooter travels 20 mph, the first friend 4 mph, and the second friend 5 mph, how far away in miles from the starting point should the man drop off the first friend and turn around? Round your answer to the nearest tenth.
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
A man with a scooter and two friends had to make a journey of 52 miles.
The man decided he would take the first friend a certain distance while the second walked.
He would drop the first friend off to walk the remainder of the 52 miles, return to meet the second friend,
pick him up, and proceed to the end of the journey finishing just as the first friend finished.
If the scooter travels 20 mph, the first friend 4 mph, and the second friend 5 mph, how far away in miles from the starting point
should the man drop off the first friend and turn around? Round your answer to the nearest tenth.
~~~~~~~~~~~~~~~
Let x be that distance from the start, the problems asks for.
Then the time of the whole journey for the first friend is
 +  hours. (1)
Then the scooter returns back to meet the second frient. Let's find time "t" for this particular trip.
We write the distance equation for the scooter returning back and the second frieng walking toward him
20t + 5t = x.
From this equation, the time to return for the scooter is t = 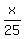 hours.
During this time t = 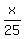hours, the seconf frient travels  =  kilometers.
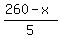So, now they together should cover  =  kilometers at the rate of 20 km/h.
It will take  =  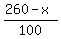hours.
Thus the total time traveling for the second friend is
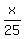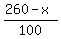+ + hours. (2)
You should identify each addend in this expression, based on my descriptions above.
Lastly, our final equation says that the time (1) is equal to the time (2)
+ = + + .
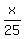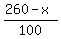At this point, I just completed setup for you.
You have now a simple linear equation to find x.
The rest is just a technique.
------------
At this point I complete my instructions.
If you will have difficulties or questions, do not hesitate ask me.
If you do, then please refer to the ID number of this problem, which is 1163721.
The ID number is the first number, which you see in your page in the UPPER LEFT corner.
If you will post to me without referring to this ID number, I will not know to whom to answer.
It is how this forum works.
So, mentioning this ID is NECESSARY, if you want to have two-way communication with me.
Good luck (!)
|
|
|
