Question 1138489: A concert manager counted 350 ticket receipts the day after the concert. The price for a student ticket was $12.50, and the price for an adult ticket was $16.00. The register confirms that $5,075 was taken in. How many student tickets and adult tickets were sold?
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39623)   (Show Source):
Answer by ikleyn(52832)  (Show Source):
You can put this solution on YOUR website! .
Let x = # of adult tickets, y = # of student tickets.
From the condition, you have these 2 equations
x + y = 350 (1) (counting tickets)
16*x + 12.50*y = 5075 (2) (counting money)
From equation (1), express y = 350 - x and substitute it into equation (2). You will get
16x + 12.50*(350-x) = 5075.
Express x and calculate answer
x = 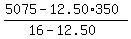 = 200.
Then from equation (1), y = 350 - 200 = 150.
ANSWER. 200 adults tickets and 150 student tickets.
CHECK. 200*16 + 150*12.50 = 5075 dollars. ! Correct !
The problem solved using 2-equation setup and the Substitution method.
--------------
It is a standard and typical ticket problem.
For ticket problems, read the lessons
- Using systems of equations to solve problems on tickets
- Three methods for solving standard (typical) problems on tickets
in this site.
From these lessons, learn on how to solve such problems once and for all.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Systems of two linear equations in two unknowns".
|
|
|
