Question 1073070: A bakery makes 600 specialty breads--multigrain and herb--each week. Standing orders from restaurants are for 100 multigrain breads and 200 herb breads. The profit on each multigrain bread is $8 and on herb bread, $10. How many breads of each type should the bakery make to maximize profit? How, if it all, do the maximum profit and optimal production policy change if the bakery has no standing orders? ---This is a linear programming problem.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website!
x = number of loaves of multigrain bread made each week.
y = number of loaves of herb bread made each week.
x + y <= 600
if they have standing orders of 100 multigrain loaves of bread and 200 herb loaves of bread, then that's the minimum that they have to make.
x >= 100
y >= 200
the constraints are:
x + y <= 600
x >= 100
y >= 200
using the www.desmos.com calculator, you would graph the opposite of these constraints and the region of the graph that is not shaded will be your region of feasibility.
in other words, you would graph:
x + y >= 600
x <= 100
y <= 200
the graph is shown below:
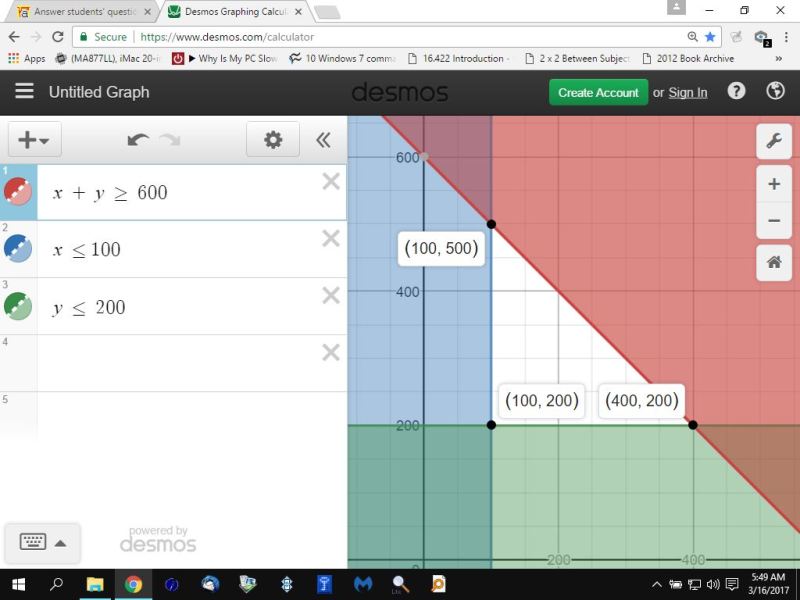
your maximum profit will be at one or more of these corner points.
at (100,500), your profit is 8 * 100 + 10 * 500 = 5800
at (100,200), your profit is 8 * 100 + 10 * 200 = 2800
at (400,200), your profit is 8 * 400 + 10 * 200 = 5200
your maximum profit will be when you make and sell 100 multigrain and 500 herb loaves of bread.
if you do not have any standing orders, then your constraint equations become:
x + y <= 600
x >= 0
y >= 0
using the www.desmos.com calculator, you would graph the opposite of these constraints and the region of the graph that is not shaded will be your region of feasibility.
in other words, you would graph:
x + y >= 600
x <= 0
y <= 0
the graph is shown below:
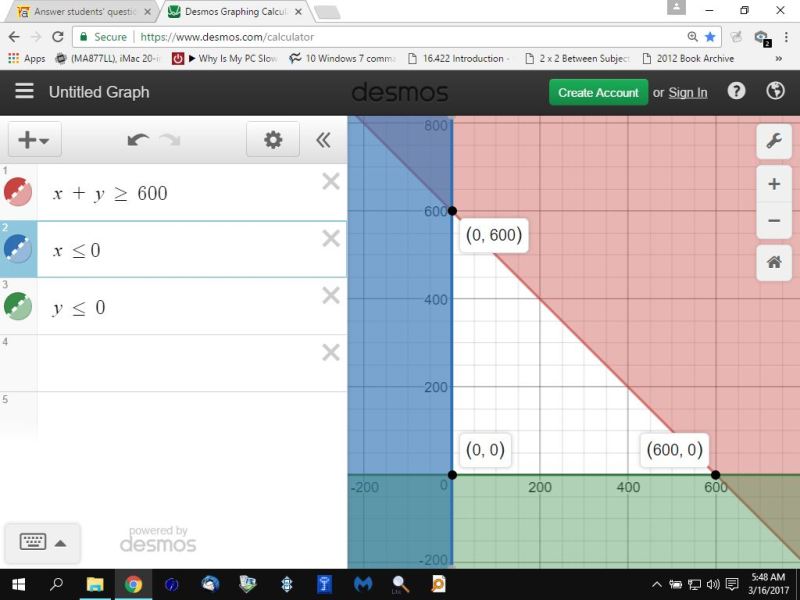
your maximum profit will be at one or more of these corner points.
at (0,600), your profit is 8 * 0 + 10 * 600 = 6000
at (0,0), your profit is 8 * 0 + 10 * 0 = 0
at (600,0), your profit is 8 * 600 + 10 * 0 = 4800
your maximum profit will be when you make and sell 0 multigrain and 600 herb loaves of bread.
your constraints have to be satisfied in order for your maximum profit solution to be realized.
when your constraints were:
x + y <= 600
x >= 100
y >= 200
at the maximum corner point of (100,500), these constraints were satisfied.
when your constraints were:
x + y <= 600
x >= 0
y >= 0
at the maximum corner point of (0,600), these constraints were satisfied.
|
|
|