Question 1011499: Brainstorming !! I send a famer to buy 100 animals with $100.00 dollars,how many off each he can buy? Ducks $10 each, pigs $3.00 each, chicks .50¢ each??
2 possible answers.
Found 4 solutions by rothauserc, Edwin McCravy, macston, KMST:
Answer by rothauserc(4718)   (Show Source):
You can put this solution on YOUR website! let d be number of ducks, p be number of pigs, c be number of chicks, then
d + p + c = 100
10d + 3p + 0.50c = 100
***************************************************************************
there are 101 solutions
reject those solutions that do not result in d + p + c = 100
**************************************************************************
multiply the first equation by -3 and add the two equations
-3d -3p -3c = -300
10d +3p +0.50c = 100
add these two equations, we get
7d -2.5c = -200
let c=a, where a is an integer from the set [0, 100]
7d -2.5a = -200
d = (2.5a - 200) / 7
**************************************************************************
now use first equation to solve for p in terms of a
(2.5a-200)/7 +p + a = 100
multiply both sides of = by 7
2.5a-200 +7p +7a = 700
9.5a +7p = 900
p = (900 -9.5a) / 7
**************************************************************************
solution set is
d=(2.5a-200)/7, p=(900-9.5a)/7, c=a
Answer by Edwin McCravy(20060)  (Show Source):
You can put this solution on YOUR website! Brainstorming !! I send a famer to buy 100 animals with
$100.00 dollars,how many off each he can buy? Ducks $10
each, pigs $3.00 each, chicks .50¢ each?? 2 possible
answers.
This is a number theory problem, three unknowns but only
2 equations with the stipulation that all 3 variables can
only be non-negative integers.
D + P + C = 100
$10.00D + $3.00P + $0.5C = $100.00
Multiply the second equation by 10 and remove the dollar signs:
100D + 30P + 5C = 1000
Divide it through by 5
1) 20D + 6P + C = 200
Solve the first equation for D = 100 - P - C
Substitute that into
20D + 6P + C = 200
20(100 - P - C) + 6P + C = 200
2000 - 20P - 20C + 6P + C = 200
2000 - 14P - 19C = 200
1800 = 14P + 19C
2) 14P + 19C = 1800
The smallest coefficient in absolute value is 14,
so we write 19 and 1800 in terms of their nearest
multiple of 14. [We divide 1800/14 = and get
approximately 128.6, so the nearest multiple of
14 to 1800 is 128*14 = 1792, so 1800 = 1792 + 8
14P + (14 + 5)C = 1792 + 8
14P + 14C + 5C = 1792 + 8
We divide each term by 14
P + C + 5C/14 = 128 + 8/14
Get the fractions on the left and the other terms
on the right:
5C/14 -8/14 = 128 - P - C
Since the right side is an integer, so is the left side.
Let that integer by A, Then
3) 5C/14 - 8/14 = A
4) 128 - P - C = A
Clear 3) of fractions
5C - 8 = 14A
5) 5C - 14A = 8
The smallest coefficient in absolute value is 5,
so we write 14 and 8 in terms of their nearest
multiple of 5.
5C - (15-1)A = 10-2
5C - 15A + A = 10-2
Divide through by 5:
C - 3A + A/5 = 2-2/5
Get the fractions on the left and the other terms
on the right:
A/5 + 2/5 = 3A - C + 2
Since the right side is an integer, so is the left side.
Let that integer by B, Then
6) A/5 + 2/5 = B
7) 3A - C + 2 = B
Clear 6) of fractions:
A + 2 = 5B
A = 5B-2
Substitute 5B-2 for A in 7)
3(5B-2) - C + 2 = B
15B - 6 - C + 2 = B
15B - 4 - C = B
14B - 4 - C = 0
14B - 4 = C
C = 14B - 4
Substitute 12B - 4 for C and 5B-2 for A in 4)
128 - P - C = A
128 - P - (14B-4) = 5B - 2
128 - P - 14B + 4 = 5B - 2
132 - P - 14B = 5B - 2
134 - 19B = P
P = 134 - 19B
Substitute 134-19B for P, 14B-4 for C, and 5B-2 for A in 1)
1) 20D + 6P + C = 200
20D + 6(134-19B) + 14B-4 = 200
20D + 804 - 114B + 14B - 4 = 200
20D + 800 - 100B = 200
20D = 100B - 600
D = 5B - 30
So
D = 5B - 30
P = 134 - 19B
C = 14B - 4
Each of those must be non-negative integers, so
5B - 30 >= 0 134 - 19B >= 0 14B - 4 >= 0
5B >= 30 -19B >= -134 14B >= 4
B >= 6 B <= 7.0526 B >= 2/7
B <= 7
Therefore B is 6 or 7
If B=6, then
First answer:
D = 5B - 30 = 5(6)-30 = 30 - 30 = 0 ducks
P = 134 - 19B = 134-19(6) = 134 - 114 = 20 pigs
C = 14B - 4 = 14(6)-4 = 84-4 = 80 chickens
If B=7, then
Second answer:
D = 5B - 30 = 5(7)-30 = 35 - 30 = 5 ducks
P = 134 - 19B = 134-19(7) = 134 - 133 = 1 pigs
C = 14B - 4 = 14(7)-4 = 98-4 = 94 chickens
Edwin
Answer by macston(5194)  (Show Source):
You can put this solution on YOUR website! .
C+D+P=100
C=100-D-P
.
$10D+$3P+$0.50C=$100
$10D+$3P+$0.50(100-D-P)=$100
$10D+$3P+$50-$0.50D-$0.50P=$100
$9.5D+$2.5P=$50
$19D+$5P=$100
$5P=$100-$19D
P=20-(19D/5)
.
Since we know P must be a positive integer (or zero,
no partial pigs), we know 19D/5 must be a
positive integer (or zero), so 19D must be evenly divisible
by 5. (i.e. , D must be a multiple of 5 - or zero)
.
For D=0:
P=20-19(0)/5=20-0=20
We have 20 pigs and no ducks.
.
For D=5:
P=20-(19(5)/5)=20-19=1
We have 1 pig and 5 ducks.
.
For D=10:
P=20-(19(10)/5)=20-38=-18
Since P is negative, this cannot be a solution
(no negative pigs, no anti-pigs)
.
.
So we have either 20 pigs and no ducks or 1 pig and 5 ducks.
.
For P=20, D=0:
C=100-D-P
C=100-0-20
C=80
ANSWER 1: We have 80 chicks, 20 pigs, and no ducks.
.
For P=1, D=5:
C=100-D-P
C=100-1-5
C=94
ANSWER 2: We have 94 chicks, 1 pig, and 5 ducks.
.
CHECK 1:
C=80; P=20; D=0
$0.50C+$3P+$10D=$100
$0.50(80)+$3(20)+$10(0)=$100
$40+$60=$100
$100=$100
Answer 1 checks.
.
CHECK 2:
C=94; P=1; D=5
$0.50C+$3P+$10D=$100
$0.50(94)+$3(1)+$10(5)=$100
$47+$3+$50=$100
$100=$100
Answer 2 checks, so we have our two solutions.
.
Answer by KMST(5328)  (Show Source):
You can put this solution on YOUR website! All approaches have their merits, and Edwin's strategy works well in all cases.
However, in this particular case,
combining that strategy with a bit of trial and error may lead to the answer faster, or easier, or in a more intuitive way.
 = number of ducks
 = number of pigs
 = number of chicks
 = total number of animals
 = total amount spend, in $.
<-->
 --> --> --> --> --> .
Choosing intelligently, we can assign values to between  and  ,
and find integers and between and .
Since  ,  does yield an integer value for ,
but  does, yielding  ,
and every  unit increase in results in a  unit reduction in ,
so  yields  , and
 yields  .
So, we could try , ,  ,
and a few more, until we get to a  .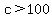
How far can we continue?
Since  ,
 is as far as we can go.
 ---> ---> is one solution.
Before getting to  we hit  , and  .
 ---> ---> ---> ---> ---> is another solution.
and lesser values do not yield solutions because they cause to be negative.
|
|
|
