Question 22721: This is a problem in the text book "Matrix Analysis and Applied Linear Algerbra"
by Carl D. Meyer. problem 6.2.14. I have the answer manual to the problem but i dont understand it. I'm not sure how to scan and paste a picture of the problem so this is the best I can do. If someone have book availible, can you explain all 3 parts of question?
By considering rank-one updated matrices, derive the following formulas.
A1 is alpha varible with subscript 1
A2 is alpha varible with subscript 2
An is alpha varible with subscript n
matrix C:
[(1+A1) A2 ......An]
[A1 (1+A2) ......An]
[.............................]= 1+A1+A2+A3+ .....+ An
[.............................]
[A1 A2.......(1+An)]
Answer by khwang(438)   (Show Source): (Show Source):
You can put this solution on YOUR website! Note: You should say that you mean to find the determinant of C and forget
about those uncommon terms as rank-one updated matrices, or alpha variables, since you should not suppose other people sitting in the same class and use the same textbook. In fact, because of that ,I replied to you a little bit tardy.
matrix C: (I change it to Cn)
[(1+A1) A2 ......An]
[A1 (1+A2) ......An]
[..................]
[A1 A2.......(1+An)]
to show det(Cn) =
|(1+A1) A2 ......An|
|A1 (1+A2) ......An|
|..................|
|A1 A2.......(1+An)|
= 1+  Ai (i from 1 to n) ...(*) Ai (i from 1 to n) ...(*)
Usually, we prove it by math. induction.
Basic, when n = 1, C1 is a 1x1 matrix, we have C1 = [1+A1]
so, det(C1) = 1 + A1, so (*) is true when n = 1.
Induction Hypothesis: Assume that (*) is true, when n = k. i.e. det(Ck) = 1+  Ai (i from 1 to k). To show det(C(k+1)) = Ai (i from 1 to k). To show det(C(k+1)) =
1+  Ai (i from 1 to k+1). Ai (i from 1 to k+1).
Since det(C(k+1))
|(1+A1) A2 ......A(k+1)|
|A1 (1+A2) ......A(k+1)|
|..................|
|A1 A2.......(1+A(k+1))|
(multiply -1 to the 1st row and add it to the n+1 th row )
=
|(1+A1) A2 ......A(k+1)|
|A1 (1+A2) ......A(k+1)|
|..................|
|-1 0.......1|
(expand along the last row)
= 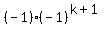
|A2 A3 ...... A(k+1)|
|(1+A2) A3......A(k+1)|
|..................|
|A2 A3 ......1+Ak A(k+1)|
+
|(1+A1) A2 ......Ak|
|A1 (1+A2) ......Ak|
|..................|
|A1 A2.......(1+Ak)|
(set the first determinant to be Bk and use Induction Hyp.)
= 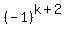 Bk + (1+ Bk + (1+  Ai ) (i from 1 to k)) Ai ) (i from 1 to k))
To compute Bk, by adding 1st row *-1 to each of the other k-1 rows, we have
|A2 A3 ...... A(k+1)|
|1 0 0..0|
|.............|
|0 0.......1 0|
, expanding along the last column, we can see that Bk =  * A(k+1) . * A(k+1) .
Hence, det(C(k+1)) = 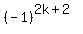 A(k+1)+ 1 + A(k+1)+ 1 +  Ai (i from 1 to k) Ai (i from 1 to k)
= 1+  Ai (i from 1 to k+1). Ai (i from 1 to k+1).
This proves that (*) is true, when n = k+1 and the induction is complete.
The idea is the same as , the case when n = 3.
Det(C3)=
|1+A1 A2 A3|
|A1 1+A2 A3|
|A1 A2 1+A3|
= |1+A1 A2 A3|
|A1 1+A2 A3|
| -1 0 1|
= (-1) | A2 A3|
|1+A2 A3|
+ det(C2)
= (-1)| A2 A3|
|1 0|
+ det(C2)
= -(-1)*A3*1 + (1+A1+A2)
= 1+A1+A2+ A3.
If you have learned eigenvalues and character polynomials,then we can have a direct proof as below.
Let Rn be the (1xn) row = [A1 A2.. An] , and the nxn matrix Un = [Rn, Rn,..Rn] (i.e. each row equals to Rn). By solving the possible eignvalues & eigenvectors of Un, we see that the char. poly. of Un = det(xI-Un)
= 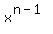 (x- (x-  Ai (i from 1 to n)). Ai (i from 1 to n)).
(Note I+Un = Cn and det(-I-Un) =  det(I + Un)) det(I + Un))
Set x =-1, we obtain det(-I-Un) = 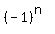 *det(Cn) = *det(Cn) =
 * (1+ * (1+  Ai (i from 1 to n)) . Ai (i from 1 to n)) .
Hence, det(Cn) = 1+  Ai (i from 1 to n). Ai (i from 1 to n).
Try to read carefully and understand the details.
Good luck !
Kenny
|
|
|