Question 20758: Recall that P3 is the space of all polynomials of degree less than three with real coefficients. Define an inner product < , > on P3 given by:
< p,q > = the sum from i=1 to 3 of p(i-1)*q(i-1), and let || || be the norm with respect to this inner product.
(a) let p(x)=1+x-x^2 and q(x)=2-x
Find a polynomial f(x) in P3 which is orthogonal to both p(x) and q(x) with respect to the inner product.
(b) find the distance between p(x)+q(x) and f(x).
thank you so much for your help!
Answer by khwang(438)   (Show Source): (Show Source):
You can put this solution on YOUR website! Recall that P3 is the space of all polynomials of degree less than three with real coefficients. Define an inner product < , > on P3 given by:
< p,q > = the sum from i=1 to 3 of p(i-1)*q(i-1), and let || || be the norm with respect to this inner product.
(a) let p(x)=1+x-x^2 and q(x)=2-x
Find a polynomial f(x) in P3 which is orthogonal to both p(x) and q(x) with respect to the inner product.
(b) find the distance between p(x)+q(x) and f(x).
[Note as regular dot product in  ] ]
Sol: a) Let f = pxq (as cross product)
= |i j k| (i as 1, j as x, k as  ) )
|1 1 -1|
|2-1 0|
= -i - 2j + -3k = 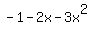
Or
Let f = a + bx + cx^2 in P3, if = = 0, then
= (a,b,c). (1,1,-1) = a+b-c = 0 &
= (a,b,c). (2,-1,0) = 2a-b = 0
then we have b=2a, c= a+b= 3a.
f = a (1+2x + 3x^2) for some a.
b) Let f(x) = 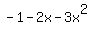
||p(x)+q(x)- f(x)|| = || (3-x^2) + 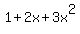 || ||
= || 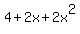 || ||
= 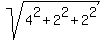
= 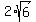
Kenny
PS: 1.Sorry for answering you late.
2.It seems that you posted this question in wrong forum.
3.You have to work hard.
|
|
|