Question 1134407: Find four numbers in A.P whose sum is 20 and the sum of whose squares is 120.
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52778)   (Show Source):
You can put this solution on YOUR website! .
The four terms of the given AP are nicely (symmetrically) located around their central point x= 5, which is their arithmetic mean  .
I will use this fact in order for to simplify the solution. I also introduce 2d as the common difference of the AP
(instead of using the tradition designation d for the common difference).
Then obviously
 = 5 - 3d,
 = 5 - d,
 = 5 + d,
 = 5 + 3d.
The sum of squares of these four terms is
 =  +  +  +  =  .
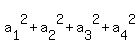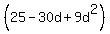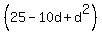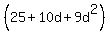So, for "d" you have this equation
100 + 20d^2 = 120,
from which you get
d^2 = 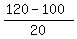 = 1; hence, d = +/- 1.
Thus the four terms of the AP are 5-3 = 2; 5-1 = 4; 5+1 = 6 and 5+3 = 8.
ANSWER. The four terms of the AP are 2, 4, 6, 8.
The reversed sequence 8, 6, 4, 2 is the solution, also. It corresponds to the value d= -1.
Solved.
-------------------
There is a bunch of lessons on arithmetic progressions in this site:
- Arithmetic progressions
- The proofs of the formulas for arithmetic progressions
- Problems on arithmetic progressions
- Word problems on arithmetic progressions
- One characteristic property of arithmetic progressions
- Solved problems on arithmetic progressions
- Math Olimpiad level problem on arithmetic progression
- Mathematical induction and arithmetic progressions
- Mathematical induction for sequences other than arithmetic or geometric
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Arithmetic progressions".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
/\/\/\/\/\/\/\/
I want to remind you that as an educated visitor, you MUST express your thanks to EACH the solution
that I produce in response to your request.
I forced to make this reminder because MANY (if not all) visitors IGNORE THIS RULE. Unfortunately.
Which I consider as an extreme degree of discourtesy.
Answer by greenestamps(13198)  (Show Source):
You can put this solution on YOUR website!
Since the sum of the four numbers and the sum of their squares are both whole numbers, the four numbers are probably whole numbers. So solve the problem using logical trial and error.
The sum of the four numbers is 20, so their average is 5. The easiest way to get and AP of four whole numbers with an average of 5 is 2, 4, 6, 8. (The AP 5, 5, 5, 5 is easier, but not very interesting; and it doesn't satisfy the other condition of the problem.)
And the AP 2, 4, 6, 8 does satisfy the other condition: 2^2+4^2+6^2+8^2 = 4+16+36+64 = 120.
So the AP is 2, 4, 6, 8.
If you need an algebraic solution, here is one that makes the algebra relatively easy.
Since the average of the four numbers is 5, and since we are guessing that the numbers are whole numbers, let the middle two numbers be 5-a and 5+a. That makes the common difference 2a, so the other two numbers are 5-3a and 5+3a.
The sum of the squares of those four numbers is
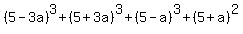
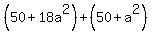
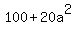
Since the sum of the squares is 120,
And so the four numbers are
5-3a = 2
5-a = 4
5+a = 6
5+3a = 8
Note when we got to the point where we had a^2=1, we could have chosen a = -1; we would have ended up with the same four numbers:
5-3a = 8
5-a = 6
5+a = 4
5+3a = 2
|
|
|
