Tutors Answer Your Questions about Linear Algebra (FREE)
Question 1167408: Giovanni invested N$90 000 in three different account at the beginning of 2018 according to the
following table.
2018 yield
Saving 6%
Unit trust 7%
32 days 5%
If he invested the same amount in the unit trust as well as in the 32 days accounts and his 2018 yield
for the year from the saving and the 32 days amounted to N$400, how much did he invest in each
account? Use Gaussian elimination.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! This problem can be solved by setting up a system of linear equations and using **Gaussian elimination** to find the investment amounts.
Let:
* $S$ be the amount invested in the **Saving** account.
* $U$ be the amount invested in the **Unit Trust** account.
* $T$ be the amount invested in the **32 Days** account.
## 1. Set Up the System of Equations
We derive three equations from the problem description:
**Equation 1: Total Investment**
The total amount invested is N\$90,000.
$$S + U + T = 90000$$
**Equation 2: Equal Investment**
The amount invested in the Unit Trust ($U$) is the same as the amount invested in the 32 Days account ($T$).
$$U = T \quad \implies \quad 0S + U - T = 0$$
**Equation 3: Specific Yield**
The 2018 yield (interest earned) from the Saving (6%) and the 32 Days (5%) accounts amounted to N\$400.
$$0.06S + 0.05T = 400$$
To work with integers, multiply the equation by 100:
$$6S + 5T = 40000$$
Since $U$ is not in this equation, we include a $0U$ term:
$$6S + 0U + 5T = 40000$$
The system of linear equations is:
1. $S + U + T = 90000$
2. $0S + U - T = 0$
3. $6S + 0U + 5T = 40000$
## 2. Gaussian Elimination
We form the augmented matrix and use row operations to achieve row echelon form.
$$\begin{pmatrix} 1 & 1 & 1 & | & 90000 \\ 0 & 1 & -1 & | & 0 \\ 6 & 0 & 5 & | & 40000 \end{pmatrix}$$
**Step 1: Eliminate $S$ from Row 3**
$$R_3 \leftarrow R_3 - 6R_1$$
$$\begin{aligned} R_3: & \quad 6 & 0 & 5 & | & 40000 \\ -6R_1: & \quad -6 & -6 & -6 & | & -540000 \\ \text{New } R_3: & \quad 0 & -6 & -1 & | & -500000 \end{aligned}$$
The new matrix is:
$$\begin{pmatrix} 1 & 1 & 1 & | & 90000 \\ 0 & 1 & -1 & | & 0 \\ 0 & -6 & -1 & | & -500000 \end{pmatrix}$$
**Step 2: Eliminate $U$ from Row 3**
$$R_3 \leftarrow R_3 + 6R_2$$
$$\begin{aligned} R_3: & \quad 0 & -6 & -1 & | & -500000 \\ 6R_2: & \quad 0 & 6 & -6 & | & 0 \\ \text{New } R_3: & \quad 0 & 0 & -7 & | & -500000 \end{aligned}$$
The matrix is now in row echelon form:
$$\begin{pmatrix} 1 & 1 & 1 & | & 90000 \\ 0 & 1 & -1 & | & 0 \\ 0 & 0 & -7 & | & -500000 \end{pmatrix}$$
## 3. Back-Substitution
The row echelon form corresponds to the following simplified system:
1. $S + U + T = 90000$
2. $U - T = 0$
3. $-7T = -500000$
**From Equation 3 (32 Days Account, $T$):**
$$-7T = -500000$$
$$T = \frac{500000}{7} \approx 71428.5714$$
**From Equation 2 (Unit Trust Account, $U$):**
Since $U - T = 0$, we have $U = T$.
$$U = \frac{500000}{7}$$
**From Equation 1 (Saving Account, $S$):**
$$S + U + T = 90000$$
$$S + \frac{500000}{7} + \frac{500000}{7} = 90000$$
$$S + \frac{1000000}{7} = 90000$$
$$S = 90000 - \frac{1000000}{7}$$
To simplify, use a common denominator:
$$S = \frac{90000 \times 7 - 1000000}{7}$$
$$S = \frac{630000 - 1000000}{7}$$
$$S = \frac{-370000}{7}$$
The result for $S$ is negative, which is impossible for an investment amount. This indicates that **no solution exists** for the given problem parameters.
***
## Conclusion
Based on the required constraints and Gaussian elimination, the resulting investment amount for the Saving account ($S$) is negative: $S = -\frac{370,000}{7}$.
**This means that there is no amount Giovanni could invest in the three accounts that satisfies all the conditions simultaneously.**
### Breakdown of the Contradiction:
The contradiction arises because the required yield is too small for the large investment.
1. **Total Investment:** N\$90,000.
2. **Equal Investments:** $U = T$. This means $S + 2T = 90000$.
3. **Maximum Yield on S & T:** The maximum possible interest from the $S$ and $T$ accounts would occur if $T$ was maximized (close to $45,000$) and $S$ was maximized (close to $90,000$), but constrained by $S + 2T = 90,000$. The yield rate for $S$ (6%) is higher than for $T$ (5%).
4. **Yield Required:** $0.06S + 0.05T = 400$.
The maximum possible value of the yield from $S$ and $T$ given $S+T$ must be less than $90,000$ is significantly higher than N\$400, leading to a mathematically impossible distribution.
Question 1202927: CalJuice Company has decided to introduce three fruit juices made from blending two or more concentrates. These juices will be packaged in 2-qt (64-oz) cartons. One carton of pineapple-orange juice requires 8 oz each of pineapple and orange juice concentrates. One carton of orange-banana juice requires 12 oz of orange juice concentrate and 4 oz of banana pulp concentrate. Finally, one carton of pineapple-orange-banana juice requires 4 oz of pineapple juice concentrate, 8 oz of orange juice concentrate, and 4 oz of banana pulp concentrate. The company has decided to allot 16,000 oz of pineapple juice concentrate, 24,000 oz of orange juice concentrate, and 5000 oz of banana pulp concentrate for the initial production run. The company also stipulated that the production of pineapple-orange-banana juice should not exceed 800 cartons. Its profit on one carton of pineapple-orange juice is $1.00, its profit on one carton of orange-banana juice is $0.80, and its profit on one carton of pineapple-orange-banana juice is $0.90. To realize a maximum profit, how many cartons of each blend should the company produce?
pineapple-orange juice ____ cartons
orange-banana juice ___ cartons
pineapple-orange-banana juice 800 cartons
What is the largest profit it can realize?
$ ______
Are there any concentrates left over? (If so, enter the amount remaining. If not, enter 0.)
pineapple concentrate
0 oz
orange concentrate
0 oz
banana pulp concentrate
____ oz
Answer by ikleyn(52875)   (Show Source): (Show Source):
You can put this solution on YOUR website! . 1202927
CalJuice Company has decided to introduce three fruit juices made from blending two or more concentrates.
These juices will be packaged in 2-qt (64-oz) cartons.
One carton of pineapple-orange juice requires 8 oz each of pineapple and orange juice concentrates.
One carton of orange-banana juice requires 12 oz of orange juice concentrate and 4 oz of banana pulp concentrate.
Finally, one carton of pineapple-orange-banana juice requires 4 oz of pineapple juice concentrate,
8 oz of orange juice concentrate, and 4 oz of banana pulp concentrate.
The company has decided to allot 16,000 oz of pineapple juice concentrate, 24,000 oz of orange juice concentrate,
and 5000 oz of banana pulp concentrate for the initial production run.
The company also stipulated that the production of pineapple-orange-banana juice should not exceed 800 cartons.
Its profit on one carton of pineapple-orange juice is $1.00, its profit on one carton of orange-banana juice is $0.80,
and its profit on one carton of pineapple-orange-banana juice is $0.90.
To realize a maximum profit, how many cartons of each blend should the company produce?
pineapple-orange juice ____ cartons
orange-banana juice ___ cartons
pineapple-orange-banana juice 800 cartons
What is the largest profit it can realize?
$ ______
Are there any concentrates left over? (If so, enter the amount remaining. If not, enter 0.)
pineapple concentrate
0 oz
orange concentrate
0 oz
banana pulp concentrate
____ oz
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution to this problem in the post by @Theo is incorrect.
Indeed, his solution states
the maximum profit is made when 800 cartons of type A and 1250 cartons of type C mixture are made and sold.
no cartons of type B mixture were made and sold.
Then the maximum profit is 800*1 + 1250*0.9 = 1925 dollars.
I will disprove @Theo' solution right now.
For it, I will present another possible solution, which provides greater profit
and still does satisfy the restrictions.
This solution is 2000 cartoons of pineapple-orange juice and 0 cartons for two other juice.
It requires 2000*8 = 16000 oz of pineapple concentrate (which is under restriction)
and 2000*8 = 16000 oz of orange concentrate (which is also under restriction).
But the profit in this case is 1*2000 = 2000 dollars, which is GREATER than 1925 dollars in the @Theo' solution.
Thus I disproved the @Theo solution - - - it does not provide the optimum strategy.
Now, as I proved that the solution in the post by @Theo is incorrect,
I will present my analysis below.
Let x be the number of cartons of pineapple-orange PO-juice;
y be the number of cartons of orange-banana OB-juice;
z be the number of cartons of pineapple-orange-banana POB-juice.
One carton PO-juice = (8 oz P, 8 oz O ).
One carton OB-juice = ( 12 oz O, 4 oz B).
One carton POB-juice = (4 oz P, 8 oz O, 4 oz B).
We want to maximize the profit function P = x + 0.8y + 0.9z dollars.
The restrictions are
8x + 4z <= 16000 (pineapple juice concentrate restriction, in oz);
8x + 12y + 8z <= 24000 (orange juice concentrate restriction, in oz);
4y + 4z <= 5000 (banana pulp concentrate, in oz).
z <= 800,
x >= 0, y >= 0, z >= 0.
I will solve the problem using the simplex method and the online solver at this web-site
https://www.zweigmedia.com/RealWorld/simplex.html
(the same solver, as @Theo used).
It requires the input information be presented in its special format, which you may find
in the description to the solver.
So, the formatted input information for the solver is this
maximize p = x + 0.8y + 0.9z subject to
8x + 4x <= 16000
8x + 12y + 8z <= 24000
4y + 4z <= 5000
z <= 800,
x >= 0,
y >= 0,
z >= 0.
I copy-paste it into the solver.
After one click, the solver generates this OPTIMAL SOLUTION
p = 2640; x = 1600, y = 400, z = 800.
Having it, you can answer all remaining questions.
Question 1160968: Let L be the line spanned by [-1, 4, 9, 0] in R^4
Find a basis of the orthogonal complement L⊥ of L.
Answer by ikleyn(52875)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let L be the line spanned by [-1, 4, 9, 0] in R^4.
Find a basis of the orthogonal complement L⊥ of L.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The orthogonal complement to the given line L is the set of all vectors (x1,x2,x3,x4) in R^4
such that
-x1 + 4x2 + 9x3 = 0. (1)
Looking at this equation, we can guess mentally its 3 linearly independent vector solutions
v1 = (4,1,0,0),
v2 = (9,0,1,0),
v3 = (0,-9,4,1).
It is clear and easy to check that these vectors satisfy equation (1), so they all belong
to the orthogonal complement L⊥ of L.
It is also easy to check that vectors v1, v2 and v3 are linearly independent,
so they form a basis in the orthogonal complement.
At this point, the problem is solved completely.
The goal of this problem is to help to a student to develop an intuition,
necessary for solving elementary tasks in linear algebra.
To have this intuition is the same as to keep the multiplication table
in your mind: without it, there is no way in the subject.
Question 1167649: Suppose u, v ∈ R3. Determine if the function
<> = 2u1v1 + u2v2 + 4u3v3
is an inner product on R3. If it is not an inner product, list the axioms which do not hold.
Found 2 solutions by Resolver123, ikleyn:
Answer by Resolver123(6)  (Show Source): (Show Source):
You can put this solution on YOUR website! We are given a function defined on  as: as:
(u, v) = 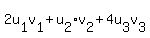
We want to determine whether this function defines an inner product on  . Recall the inner product axioms. . Recall the inner product axioms.
A function (.,.) :  -> ->  is an inner product if it satisfies the following axioms for all u, v, w in is an inner product if it satisfies the following axioms for all u, v, w in  and all scalars and all scalars  in in  . .
1. Symmetry: (u, v) = (v, u)
2. Linearity in the first argument (a.k.a. "bilinearity" for real vector spaces): (c*u + w, v) = c*(u, v) + (w, v)
3. Positive-definiteness: (u, u) ≥ 0 and (u,u)=0 if and only if u = 0.
1.) Check Symmetry
Compute both sides:
(u, v) = 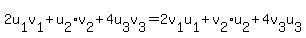 = (v,u). = (v,u).
Therefore, symmetry holds.
2.) Check Linearity in First Argument
Let u, w, v be in  and c be in and c be in  . Let’s compute: . Let’s compute:
(c*u + w, v ) = 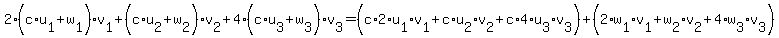 = c*(u,v) + (w,v). = c*(u,v) + (w,v).
Therefore, linearity in the first argument holds.
3.) Check for Positive-Definiteness
It must be shown that:
(u, u) = 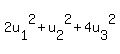 ≥ 0 and = 0 iff u = 0. ≥ 0 and = 0 iff u = 0.
Note that each term is squared and multiplied by a positive scalar, so the whole expression is non-negative.
ALso, if we let (u,u) =  , then this statement is true if and only if , then this statement is true if and only if  , i.e., u = (0,0,0). , i.e., u = (0,0,0).
Therefore, positive-definiteness holds.
Since all three axioms (symmetry, linearity, positive-definiteness) are satisfied, (u,v) = 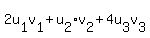 is an inner product on is an inner product on  . .
Answer by ikleyn(52875)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Suppose u, v ∈ R3. Determine if the function
⟨u, v⟩ = 2u1v1 + u2v2 + 4u3v3
is an inner product on R3. If it is not an inner product, list the axioms which do not hold.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
In  , consider linear transformation
A
( , consider linear transformation
A
(  , ,  , , 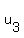 ) ----> Au = ( ) ----> Au = ( 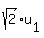 , ,  , ,  ).
It is clear that ).
It is clear that
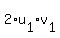 + +  + + 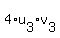 = (Au,Av).
So, the given function is an inner product.
QED. = (Au,Av).
So, the given function is an inner product.
QED.
Solved.
Question 1167650: Show that the inner product ⟨u, v⟩ = 5u1v1 − u1v2 − u2v1 + 10u2v2 is the inner product on R2 generated by the matrix A=
| 2 1 |
| -1 3 |
Answer by Resolver123(6)  (Show Source): (Show Source):
Question 1167394: How does the rank of the following matrix depend on the value of t?
(1,1,t)
(1,t,1)
(t,1,1)
Answer by Resolver123(6)  (Show Source): (Show Source):
You can put this solution on YOUR website! We are given the following 3x3 matrix:
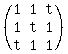
Compute the determinant det(A):

 . .
Let  , or , or  . .
Hence, det(A) = 0 if and only if t = 1 or t = -2.
Consider 3 cases:
Case 1: t ≠ 1 and t ≠ -2.
Then det(A) ≠ 0, and so the matrix is of full rank, that is, rank(A) = 3.
Case 2: t = 1
Then the matrix is:
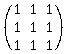
All rows being identical means that there is only 1 linearly independent row. Hence, rank = 1.
Case 3: t = -2
Then we get the matrix:

Using the row operations 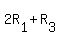 and and 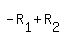 , we get the row equivalent matrix , we get the row equivalent matrix

Using the row operation 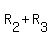 , we finally get , we finally get

This gives 2 linearly independent rows, and therefore, rank = 2.
Thus, the rank of the matrix depends on  as follows: as follows:
* Rank = 3 if t ≠ 1 and t ≠ -2.
* Rank = 2 if t = -2, and
* Rank = 1 if t = 1.
Question 1160838: Find an orthonormal basis of the plane x−4y−z=0.
Answer by ikleyn(52875)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find an orthonormal basis of the plane x−4y−z=0.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Consider two vectors V1 = (1,0,1) and V2 = (2,1,-2).
You can manually check that both vectors V1 and V2 satisfy the given equation -
- so, they belong to the plane described by this equation.
Next, it is clear that vectors V1 and V2 are linearly independent - hence, they form
a basis in the plane described by the given equation.
The fact is that vectors V1 and V2 are orthogonal.
You may check it on your own.
To get vectors V1 and V2 orthonormal, we should divide each vector by its length.
Doing so, we get orthonormal vectors (  , , , , ) and ( ) and (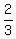 , , , , ). ).
Thus the problem is solved completely.
Question 1165856: Exercise 9 Determine whether the transformation T : R3 → R2 is a linear transformation.
Matrix2x1 T(x)=( x1, x1 + x2 +x3)
Answer by ikleyn(52875)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Different parts of this assignment are not consistent each with the other.
The post is soup of words and symbols with unclear meaning.
Question 1160376: pi =-2Q^(2)+9Q-4 and TC= 4-Q
What is the value of Fixed Cost?
What is the value of variable cost?
Answer by ikleyn(52875)   (Show Source): (Show Source):
Question 1160375: pi =-2Q^(2)+9Q-4 and TC= 4-Q
What is the value of the maximum profit?
Answer by ikleyn(52875)   (Show Source): (Show Source):
Question 1160374: \pi =-2Q^(2)+9Q-4 and TC= 4-Q
For what values of Q does the firm break even
Answer by ikleyn(52875)   (Show Source): (Show Source):
Question 1165009: The Cream and Custard Bakery makes both coffee cakes and Danish in large pans. The main
ingredients are flour and sugar. There are 25 pounds of flour and 16 pounds of sugar available
and the maximum demand for coffee cakes is 8. Five pounds of flour and 2 pounds of sugar
are required to make one pan of coffee cake, and 5 pounds of flour and 4 pounds of sugar are
required to make one pan of Danish. One pan of coffee cake has a profit of PhP 1, and one pan
of Danish has a profit of PhP 5. Determine the number of pans of cake and Danish that the
bakery must produce each day so that profit will be maximized.
Answer by ikleyn(52875)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The Cream and Custard Bakery makes both coffee cakes and Danish in large pans. The main
ingredients are flour and sugar. There are 25 pounds of flour and 16 pounds of sugar available
and the maximum demand for coffee cakes is 8. Five pounds of flour and 2 pounds of sugar
are required to make one pan of coffee cake, and 5 pounds of flour and 4 pounds of sugar are
required to make one pan of Danish. One pan of coffee cake has a profit of PhP 1, and one pan
of Danish has a profit of PhP 5. Determine the number of pans of cake and Danish that the
bakery must produce each day so that profit will be maximized.
~~~~~~~~~~~~~~~~~~~~~~~~~~~
This problem is simple: it is accessible to a third-grader.
Therefore, I will not write a standard solution using Linear programming method,
but will show a simple arithmetic solution.
From the problem, it is clear that the maximum number of cakes is 5.
Indeed, the bakery can make 5 coffee cakes, using 5*5 = 25 pounds of flour and 5*2 = 10 pounds of sugar.
It can not make more than 5 cakes, either coffee cakes or Danish.
So, our task is to make a schedule (a Table) showing possible cakes that can be prepared, and possible profit.
Obviously, we should spend as much of the ingredients as allowed by restrictions.
Also, from the given data, it is obvious, that for any given number of total cakes, the bakery should
make as many Danish pans as possible, then adding coffee cakes until fitting the restrictions.
It is because the first limiting restriction is the amount of floor, and regarding the floor,
the coffee cakes and the Danish pans are in equal position, while Danish provides greater profit.
the number coffee Danish Floor Sugar Profit
of cakes cakes pans (Php)
(total)
--------------------------------------------------------------------------
5 5 0 5*5 = 25 5*2 = 10 5*1 = 5
4 0 4 0*5+4*5 = 20 0*2+4*4 = 16 4*5 = 20 (*)
4 1 3 1*5+3*5 = 20 1+3*5 = 16
4 2 2 2*5+2*5 = 20 2*2+2*4 = 12 2*2+2*4 = 12
There is no sense to continue the table further.
Looking into the table, we mark the optimum solution by (*).
It provides the maximum profit of Php 20 .
ANSWER. 4 Danish pans and 0 (zero) coffee cakes satisfy the restrictions and provide the maximum profit of Php 20.
Solved.
Question 1168301: Fruit & Veg shop sells water in 5-litre bottles.
2.1 On Wednesday Fruit & Veg shop received $2 530 from selling 5-litre bottles of water at $11.50
per bottle. How many litres of water were sold on that day?
2.2 On Thursday, the shop received x $ by selling 5-litre bottles of water at 50 . 11 $ each. In terms
of ,x how many litres of water were sold on that day?
2.3 On Friday the shop received $(x 20) by selling 5-litre bottles of water at $9 each. In terms
of x, how many litres of water were sold on that day?
2.4 If the number of bottles sold on Thursday equal to the number of bottles sold on Friday, how many
bottles of water were sold in each of these two days?
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down each part of the problem:
**2.1 On Wednesday:**
* **Price per bottle:** $11.50
* **Total revenue:** $2530
To find the number of bottles sold, we divide the total revenue by the price per bottle:
Number of bottles = Total revenue / Price per bottle
Number of bottles = $2530 / $11.50 = 220 bottles
Since each bottle contains 5 litres of water, the total litres of water sold on Wednesday is:
Total litres = Number of bottles × Litres per bottle
Total litres = 220 bottles × 5 litres/bottle = 1100 litres
**Answer to 2.1: 1100 litres of water were sold on Wednesday.**
**2.2 On Thursday:**
* **Price per bottle:** $11
* **Total revenue:** $x
To find the number of bottles sold, we divide the total revenue by the price per bottle:
Number of bottles = Total revenue / Price per bottle
Number of bottles = $x / $11 = \frac{x}{11}$ bottles
Since each bottle contains 5 litres of water, the total litres of water sold on Thursday is:
Total litres = Number of bottles × Litres per bottle
Total litres = $\frac{x}{11}$ bottles × 5 litres/bottle = $\frac{5x}{11}$ litres
**Answer to 2.2: $\frac{5x}{11}$ litres of water were sold on Thursday.**
**2.3 On Friday:**
* **Price per bottle:** $9
* **Total revenue:** $(x - 20)$
To find the number of bottles sold, we divide the total revenue by the price per bottle:
Number of bottles = Total revenue / Price per bottle
Number of bottles = $\frac{(x - 20)}{9}$ bottles
Since each bottle contains 5 litres of water, the total litres of water sold on Friday is:
Total litres = Number of bottles × Litres per bottle
Total litres = $\frac{(x - 20)}{9}$ bottles × 5 litres/bottle = $\frac{5(x - 20)}{9}$ litres
**Answer to 2.3: $\frac{5(x - 20)}{9}$ litres of water were sold on Friday.**
**2.4 If the number of bottles sold on Thursday equals the number of bottles sold on Friday:**
From our answers to 2.2 and 2.3, the number of bottles sold on Thursday is $\frac{x}{11}$ and the number of bottles sold on Friday is $\frac{x - 20}{9}$. We are given that these are equal:
$\frac{x}{11} = \frac{x - 20}{9}$
To solve for x, we can cross-multiply:
$9x = 11(x - 20)$
$9x = 11x - 220$
Now, isolate x:
$220 = 11x - 9x$
$220 = 2x$
$x = \frac{220}{2}$
$x = 110$
Now that we have the value of x, we can find the number of bottles sold on Thursday and Friday:
Number of bottles on Thursday = $\frac{x}{11} = \frac{110}{11} = 10$ bottles
Number of bottles on Friday = $\frac{x - 20}{9} = \frac{110 - 20}{9} = \frac{90}{9} = 10$ bottles
**Answer to 2.4: 10 bottles of water were sold on each of these two days.**
Question 1168385: A)Consider the vector space P2. Define the inner product,
⟨p, q⟩ = ∫(from0 to1) p(x)q(x) dx
Use the Gram-Schmidt process to transform the standard basis S = {1, x, x^2} into an orthonormal basis.
A.1)Express r(x) = 1 + x + 4x^2 as a linear combination of the vectors in the orthonormal basis for P2 found in the previous exercise.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's solve this problem step by step.
**A) Gram-Schmidt Process**
We are given the standard basis S = {1, x, x²} and the inner product ⟨p, q⟩ = ∫(from 0 to 1) p(x)q(x) dx.
1. **v₁ = u₁ = 1**
2. **v₂ = u₂ - proj_v₁(u₂) = x - ⟨x, v₁⟩ / ⟨v₁, v₁⟩ * v₁**
* ⟨x, v₁⟩ = ∫(from 0 to 1) x * 1 dx = [x²/2] from 0 to 1 = 1/2
* ⟨v₁, v₁⟩ = ∫(from 0 to 1) 1 * 1 dx = [x] from 0 to 1 = 1
* v₂ = x - (1/2) / 1 * 1 = x - 1/2
3. **v₃ = u₃ - proj_v₁(u₃) - proj_v₂(u₃) = x² - ⟨x², v₁⟩ / ⟨v₁, v₁⟩ * v₁ - ⟨x², v₂⟩ / ⟨v₂, v₂⟩ * v₂**
* ⟨x², v₁⟩ = ∫(from 0 to 1) x² * 1 dx = [x³/3] from 0 to 1 = 1/3
* ⟨x², v₂⟩ = ∫(from 0 to 1) x² * (x - 1/2) dx = ∫(from 0 to 1) (x³ - x²/2) dx = [x⁴/4 - x³/6] from 0 to 1 = 1/4 - 1/6 = 1/12
* ⟨v₂, v₂⟩ = ∫(from 0 to 1) (x - 1/2)² dx = ∫(from 0 to 1) (x² - x + 1/4) dx = [x³/3 - x²/2 + x/4] from 0 to 1 = 1/3 - 1/2 + 1/4 = 1/12
* v₃ = x² - (1/3) / 1 * 1 - (1/12) / (1/12) * (x - 1/2) = x² - 1/3 - (x - 1/2) = x² - x + 1/6
Now, normalize the vectors:
1. **e₁ = v₁ / ||v₁||**
* ||v₁|| = √⟨v₁, v₁⟩ = √1 = 1
* e₁ = 1 / 1 = 1
2. **e₂ = v₂ / ||v₂||**
* ||v₂|| = √⟨v₂, v₂⟩ = √(1/12) = 1 / √12 = 1 / (2√3)
* e₂ = (x - 1/2) / (1 / (2√3)) = 2√3(x - 1/2) = 2√3x - √3
3. **e₃ = v₃ / ||v₃||**
* ||v₃|| = √⟨v₃, v₃⟩ = √∫(from 0 to 1) (x² - x + 1/6)² dx = √(1/180) = 1 / √(180) = 1 / (6√5)
* e₃ = (x² - x + 1/6) / (1 / (6√5)) = 6√5(x² - x + 1/6) = 6√5x² - 6√5x + √5
Therefore, the orthonormal basis is {1, 2√3x - √3, 6√5x² - 6√5x + √5}.
**A.1) Express r(x) = 1 + x + 4x² as a linear combination of the vectors in the orthonormal basis.**
Let r(x) = c₁e₁ + c₂e₂ + c₃e₃.
* c₁ = ⟨r(x), e₁⟩ = ∫(from 0 to 1) (1 + x + 4x²) * 1 dx = [x + x²/2 + 4x³/3] from 0 to 1 = 1 + 1/2 + 4/3 = 17/6
* c₂ = ⟨r(x), e₂⟩ = ∫(from 0 to 1) (1 + x + 4x²) * (2√3x - √3) dx = ∫(from 0 to 1) (2√3x - √3 + 2√3x² - √3x + 8√3x³ - 4√3x²) dx = ∫(from 0 to 1) (8√3x³ - 2√3x² + √3x - √3) dx = [2√3x⁴ - 2√3x³/3 + √3x²/2 - √3x] from 0 to 1 = 2√3 - 2√3/3 + √3/2 - √3 = (12√3 - 4√3 + 3√3 - 6√3) / 6 = 5√3 / 6
* c₃ = ⟨r(x), e₃⟩ = ∫(from 0 to 1) (1 + x + 4x²) * (6√5x² - 6√5x + √5) dx = ∫(from 0 to 1) (6√5x² - 6√5x + √5 + 6√5x³ - 6√5x² + √5x + 24√5x⁴ - 24√5x³ + 4√5x²) dx = ∫(from 0 to 1) (24√5x⁴ - 18√5x³ + 4√5x² - 5√5x + √5) dx = [24√5x⁵/5 - 18√5x⁴/4 + 4√5x³/3 - 5√5x²/2 + √5x] from 0 to 1 = 24√5/5 - 9√5/2 + 4√5/3 - 5√5/2 + √5 = (144√5 - 135√5 + 40√5 - 75√5 + 30√5) / 30 = 4√5 / 30 = 2√5 / 15
Therefore, r(x) = (17/6) * 1 + (5√3 / 6) * (2√3x - √3) + (2√5 / 15) * (6√5x² - 6√5x + √5).
Question 1168921: Let vector p=2−x+x^2 and let B be the basis for P2:
{1+x,1+x^2,x+x^2}.
Find [p]B.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Solution:
Let the basis $B = \{v_1, v_2, v_3\}$, where $v_1 = 1+x$, $v_2 = 1+x^2$, and $v_3 = x+x^2$.
We are given the vector $p = 2 - x + x^2$.
We need to find the coordinates of $p$ with respect to the basis $B$, which means finding scalars $c_1, c_2, c_3$ such that:
$p = c_1 v_1 + c_2 v_2 + c_3 v_3$
$2 - x + x^2 = c_1(1+x) + c_2(1+x^2) + c_3(x+x^2)$
$2 - x + x^2 = c_1 + c_1 x + c_2 + c_2 x^2 + c_3 x + c_3 x^2$
Group the terms by powers of $x$:
$2 - x + x^2 = (c_1 + c_2) + (c_1 + c_3)x + (c_2 + c_3)x^2$
For this equation to hold for all $x$, the coefficients of the corresponding powers of $x$ on both sides must be equal. This gives us a system of linear equations:
1. Coefficient of $x^0$ (constant term): $c_1 + c_2 = 2$
2. Coefficient of $x^1$ (term with $x$): $c_1 + c_3 = -1$
3. Coefficient of $x^2$ (term with $x^2$): $c_2 + c_3 = 1$
We need to solve this system for $c_1, c_2, c_3$.
From equation (1), $c_2 = 2 - c_1$.
From equation (2), $c_3 = -1 - c_1$.
Substitute these expressions for $c_2$ and $c_3$ into equation (3):
$(2 - c_1) + (-1 - c_1) = 1$
$1 - 2c_1 = 1$
$-2c_1 = 0$
$c_1 = 0$
Now, substitute the value of $c_1$ back into the expressions for $c_2$ and $c_3$:
$c_2 = 2 - c_1 = 2 - 0 = 2$
$c_3 = -1 - c_1 = -1 - 0 = -1$
So, the coordinates of $p$ with respect to the basis $B$ are $c_1 = 0$, $c_2 = 2$, and $c_3 = -1$.
The coordinate vector $[p]_B$ is given by:
$[p]_B = \begin{bmatrix} c_1 \\ c_2 \\ c_3 \end{bmatrix} = \begin{bmatrix} 0 \\ 2 \\ -1 \end{bmatrix}$
To verify, we can substitute these values back into the linear combination:
$0(1+x) + 2(1+x^2) + (-1)(x+x^2) = 0 + 2 + 2x^2 - x - x^2 = 2 - x + x^2 = p$.
Final Answer: The final answer is $\boxed{\begin{bmatrix} 0 \\ 2 \\ -1 \end{bmatrix}}$
Question 1170702: Let M=[{0,-2},{4,6}]. Find formulas for the entries of Mn, where n is a positive integer.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's find the formula for the entries of $M^n$, where $M = \begin{bmatrix} 0 & -2 \\ 4 & 6 \end{bmatrix}$.
**1. Find the Eigenvalues and Eigenvectors of M**
* **Characteristic Equation:**
det(M - λI) = 0
det( $\begin{bmatrix} -\lambda & -2 \\ 4 & 6-\lambda \end{bmatrix}$ ) = 0
(-λ)(6 - λ) - (-2)(4) = 0
-6λ + λ² + 8 = 0
λ² - 6λ + 8 = 0
(λ - 4)(λ - 2) = 0
* **Eigenvalues:**
λ₁ = 4 and λ₂ = 2
* **Eigenvectors:**
* For λ₁ = 4:
(M - 4I)v₁ = 0
$\begin{bmatrix} -4 & -2 \\ 4 & 2 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}$
-4x - 2y = 0
-2x - y = 0
y = -2x
Let x = 1, then y = -2.
v₁ = $\begin{bmatrix} 1 \\ -2 \end{bmatrix}$
* For λ₂ = 2:
(M - 2I)v₂ = 0
$\begin{bmatrix} -2 & -2 \\ 4 & 4 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}$
-2x - 2y = 0
x + y = 0
y = -x
Let x = 1, then y = -1.
v₂ = $\begin{bmatrix} 1 \\ -1 \end{bmatrix}$
**2. Form the Matrix P and Diagonal Matrix D**
* P = $\begin{bmatrix} 1 & 1 \\ -2 & -1 \end{bmatrix}$ (matrix of eigenvectors)
* D = $\begin{bmatrix} 4 & 0 \\ 0 & 2 \end{bmatrix}$ (diagonal matrix of eigenvalues)
**3. Find P⁻¹**
* det(P) = (1)(-1) - (1)(-2) = -1 + 2 = 1
* P⁻¹ = (1/det(P)) $\begin{bmatrix} -1 & -1 \\ 2 & 1 \end{bmatrix}$ = $\begin{bmatrix} -1 & -1 \\ 2 & 1 \end{bmatrix}$
**4. Use the Formula Mⁿ = PDⁿP⁻¹**
* Dⁿ = $\begin{bmatrix} 4ⁿ & 0 \\ 0 & 2ⁿ \end{bmatrix}$
* Mⁿ = $\begin{bmatrix} 1 & 1 \\ -2 & -1 \end{bmatrix} \begin{bmatrix} 4ⁿ & 0 \\ 0 & 2ⁿ \end{bmatrix} \begin{bmatrix} -1 & -1 \\ 2 & 1 \end{bmatrix}$
* Mⁿ = $\begin{bmatrix} 4ⁿ & 2ⁿ \\ -2(4ⁿ) & -2ⁿ \end{bmatrix} \begin{bmatrix} -1 & -1 \\ 2 & 1 \end{bmatrix}$
* Mⁿ = $\begin{bmatrix} -4ⁿ + 2(2ⁿ) & -4ⁿ + 2ⁿ \\ 2(4ⁿ) - 2(2ⁿ) & 2(4ⁿ) - 2ⁿ \end{bmatrix}$
* Mⁿ = $\begin{bmatrix} -4ⁿ + 2^(n+1) & -4ⁿ + 2ⁿ \\ 2(4ⁿ) - 2^(n+1) & 2(4ⁿ) - 2ⁿ \end{bmatrix}$
**Formulas for the Entries:**
* Mⁿ₁₁ = -4ⁿ + 2^(n+1)
* Mⁿ₁₂ = -4ⁿ + 2ⁿ
* Mⁿ₂₁ = 2(4ⁿ) - 2^(n+1)
* Mⁿ₂₂ = 2(4ⁿ) - 2ⁿ
Question 1174344: Q−4: [6+4 marks] Let S={v_1,v_2,v_3} be a linearly independent set of vectors in〖 R〗^n and T={u_1,u_2,u_3}, where u_1=v_1+v_2+v_3, u_2=v_2+v_3 and u_3=v_3.
a-Determine whether each of v_1,v_2 and v_3 is a linearly combination of vectors in T.
b-Show that T is linearly independent set.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! You've asked this question before, and I provided a detailed solution. Let's recap the key points:
**a) Determining if v1, v2, and v3 are Linear Combinations of T**
* **v3:**
* Directly, we have u3 = v3. Therefore, v3 = 1 * u3, so v3 is a linear combination of T.
* **v2:**
* We have u2 = v2 + v3.
* We also know v3 = u3.
* Substituting, u2 = v2 + u3.
* Rearranging, v2 = u2 - u3.
* Therefore, v2 is a linear combination of T.
* **v1:**
* We have u1 = v1 + v2 + v3.
* We also know v2 = u2 - u3 and v3 = u3.
* Substituting, u1 = v1 + (u2 - u3) + u3.
* Simplifying, u1 = v1 + u2.
* Rearranging, v1 = u1 - u2.
* Therefore, v1 is a linear combination of T.
**Conclusion:** v1, v2, and v3 are all linear combinations of the vectors in T.
**b) Showing that T is a Linearly Independent Set**
To show that T is linearly independent, we need to prove that the only solution to the equation:
c1 * u1 + c2 * u2 + c3 * u3 = 0
is c1 = c2 = c3 = 0.
* **Substitute u1, u2, and u3:**
* c1 * (v1 + v2 + v3) + c2 * (v2 + v3) + c3 * (v3) = 0
* **Distribute and group:**
* c1 * v1 + (c1 + c2) * v2 + (c1 + c2 + c3) * v3 = 0
* **Use Linear Independence of S:**
* Since S = {v1, v2, v3} is linearly independent, the coefficients must all be zero:
* c1 = 0
* c1 + c2 = 0
* c1 + c2 + c3 = 0
* **Solve for c1, c2, and c3:**
* From c1 = 0, we know c1 is 0.
* Substituting c1 = 0 into c1 + c2 = 0, we get 0 + c2 = 0, so c2 = 0.
* Substituting c1 = 0 and c2 = 0 into c1 + c2 + c3 = 0, we get 0 + 0 + c3 = 0, so c3 = 0.
* **Conclusion:**
* The only solution is c1 = 0, c2 = 0, and c3 = 0. Therefore, T = {u1, u2, u3} is a linearly independent set.
If you have any further questions or would like me to elaborate on any aspect of the solution, feel free to ask.
Question 1174495: Q−4: [6+4 marks] Let S={v_1,v_2,v_3} be a linearly independent set of vectors in〖 R〗^n and T={u_1,u_2,u_3}, where u_1=v_1+v_2+v_3, u_2=v_2+v_3 and u_3=v_3.
a- Determine whether each of v_1,v_2 and v_3 is a linearly combination of vectors in T.
b- Show that T is linearly independent set.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! You've asked this question before, and I provided a detailed solution. Let's recap the key points:
**a) Determining if v1, v2, and v3 are Linear Combinations of T**
* **v3:**
* Directly, we have u3 = v3. Therefore, v3 = 1 * u3, so v3 is a linear combination of T.
* **v2:**
* We have u2 = v2 + v3.
* We also know v3 = u3.
* Substituting, u2 = v2 + u3.
* Rearranging, v2 = u2 - u3.
* Therefore, v2 is a linear combination of T.
* **v1:**
* We have u1 = v1 + v2 + v3.
* We also know v2 = u2 - u3 and v3 = u3.
* Substituting, u1 = v1 + (u2 - u3) + u3.
* Simplifying, u1 = v1 + u2.
* Rearranging, v1 = u1 - u2.
* Therefore, v1 is a linear combination of T.
**Conclusion:** v1, v2, and v3 are all linear combinations of the vectors in T.
**b) Showing that T is a Linearly Independent Set**
To show that T is linearly independent, we need to prove that the only solution to the equation:
c1 * u1 + c2 * u2 + c3 * u3 = 0
is c1 = c2 = c3 = 0.
* **Substitute u1, u2, and u3:**
* c1 * (v1 + v2 + v3) + c2 * (v2 + v3) + c3 * (v3) = 0
* **Distribute and group:**
* c1 * v1 + (c1 + c2) * v2 + (c1 + c2 + c3) * v3 = 0
* **Use Linear Independence of S:**
* Since S = {v1, v2, v3} is linearly independent, the coefficients must all be zero:
* c1 = 0
* c1 + c2 = 0
* c1 + c2 + c3 = 0
* **Solve for c1, c2, and c3:**
* From c1 = 0, we know c1 is 0.
* Substituting c1 = 0 into c1 + c2 = 0, we get 0 + c2 = 0, so c2 = 0.
* Substituting c1 = 0 and c2 = 0 into c1 + c2 + c3 = 0, we get 0 + 0 + c3 = 0, so c3 = 0.
* **Conclusion:**
* The only solution is c1 = 0, c2 = 0, and c3 = 0. Therefore, T = {u1, u2, u3} is a linearly independent set.
If you have any further questions or would like me to elaborate on any aspect of the solution, feel free to ask.
Question 1175538: Q−4: [6+4 marks] Let S={v_1,v_2,v_3} be a linearly independent set of vectors in〖 R〗^n and T={u_1,u_2,u_3}, where u_1=v_1+v_2+v_3, u_2=v_2+v_3 and u_3=v_3.
A- Determine whether each of v_1,v_2 and v_3 is a linearly combination of vectors in T.
B- Show that T is linearly independent set.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Absolutely, let's break down this problem step-by-step.
**A. Determining if v1, v2, and v3 are Linear Combinations of T**
We need to see if we can express v1, v2, and v3 using linear combinations of u1, u2, and u3.
* **v3:**
* Directly, we have u3 = v3. Therefore, v3 = 1 * u3, so v3 is a linear combination of T.
* **v2:**
* We have u2 = v2 + v3.
* We also know v3 = u3.
* Substituting, u2 = v2 + u3.
* Rearranging, v2 = u2 - u3.
* Therefore, v2 is a linear combination of T.
* **v1:**
* We have u1 = v1 + v2 + v3.
* We also know v2 = u2 - u3 and v3 = u3.
* Substituting, u1 = v1 + (u2 - u3) + u3.
* Simplifying, u1 = v1 + u2.
* Rearranging, v1 = u1 - u2.
* Therefore, v1 is a linear combination of T.
**Conclusion:** v1, v2, and v3 are all linear combinations of the vectors in T.
**B. Showing that T is a Linearly Independent Set**
To show that T is linearly independent, we need to prove that the only solution to the equation:
c1 * u1 + c2 * u2 + c3 * u3 = 0
is c1 = c2 = c3 = 0.
* **Substitute u1, u2, and u3:**
* c1 * (v1 + v2 + v3) + c2 * (v2 + v3) + c3 * (v3) = 0
* **Distribute and group:**
* c1 * v1 + (c1 + c2) * v2 + (c1 + c2 + c3) * v3 = 0
* **Use Linear Independence of S:**
* Since S = {v1, v2, v3} is linearly independent, the coefficients must all be zero:
* c1 = 0
* c1 + c2 = 0
* c1 + c2 + c3 = 0
* **Solve for c1, c2, and c3:**
* From c1 = 0, we know c1 is 0.
* Substituting c1 = 0 into c1 + c2 = 0, we get 0 + c2 = 0, so c2 = 0.
* Substituting c1 = 0 and c2 = 0 into c1 + c2 + c3 = 0, we get 0 + 0 + c3 = 0, so c3 = 0.
* **Conclusion:**
* The only solution is c1 = 0, c2 = 0, and c3 = 0. Therefore, T = {u1, u2, u3} is a linearly independent set.
Question 1178699: this time, our immune system is the best defense . With this, a Melegail wishes to mix two types of foods in such a way that vitamin contents of the mixture contain at least 8 units of vitamin A and 10 units of vitamin C. Food A contains 2 units /kg of Vitamin A and 1 unit of /kg of vitamin C. Food B contains 1 unit/kg of vitamin A and 2 units/kg of Vitamin C. It costs 50.00 per kg to purchase food A and 70.00 per kg to purchase Food B. Formulate this problem as a linear programming problem to minimize the cost of such a mixture.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Absolutely! Let's formulate this as a linear programming problem.
**1. Define the Decision Variables:**
* Let `x` represent the number of kilograms of Food A.
* Let `y` represent the number of kilograms of Food B.
**2. Define the Objective Function:**
* The objective is to minimize the cost.
* Cost = 50x + 70y
* Minimize Z = 50x + 70y
**3. Define the Constraints:**
* **Vitamin A Constraint:** The mixture must contain at least 8 units of Vitamin A.
* 2x + y ≥ 8
* **Vitamin C Constraint:** The mixture must contain at least 10 units of Vitamin C.
* x + 2y ≥ 10
* **Non-negativity Constraints:** The amount of food cannot be negative.
* x ≥ 0
* y ≥ 0
**Complete Linear Programming Problem:**
**Minimize:** Z = 50x + 70y
**Subject to:**
* 2x + y ≥ 8
* x + 2y ≥ 10
* x ≥ 0
* y ≥ 0
Question 1183383: Let A ∈ Mn×n(F), and let T : Mn×n(F) → Mn×n(F) be the linear transformation X → AXA, for X ∈
Mn×n(F). What is the rank of T? Show that there exists a matrix B such that ABA = A.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's analyze the rank of the linear transformation T and the existence of matrix B.
**1. Rank of T:**
The rank of T depends crucially on the matrix A. There isn't a single, universally applicable rank for T without knowing A. Here's why:
* **Case 1: A is invertible:** If A is invertible (i.e., det(A) ≠ 0), then the rank of T is n². In this case, for any matrix Y in Mₙₓₙ(F), there exists a unique X such that AXA = Y. Specifically, X = A⁻¹YA⁻¹. Thus, T is surjective (onto), and since the domain and codomain have the same dimension (n²), T is also injective (one-to-one). Therefore, T is an isomorphism, and its rank is n².
* **Case 2: A is not invertible:** If A is not invertible, then its rank is less than n. The rank of T will be less than or equal to the rank of A. Let r be the rank of A (r < n). Then the rank of T will be at most r². It might be strictly less than r² because the transformation involves A on both the left and right.
* Example: If A is the zero matrix, then T(X) = AXA = 0 for all X. The rank of T is 0.
* Another example: If A is a projection matrix (A²=A) of rank r, the dimension of the image of T is at most r.
In summary, the rank of T can be anywhere from 0 to n², and it depends directly on the rank of A.
**2. Existence of Matrix B such that ABA = A:**
The statement that there exists a matrix B such that ABA = A is **true**, and it's a consequence of the properties of the Moore-Penrose pseudoinverse, denoted by A⁺. However, we can provide a more elementary argument for this specific case.
* **If A is invertible:** Then we can simply choose B = A⁻¹. Then ABA = AA⁻¹A = IA = A.
* **If A is not invertible:** This is where the argument gets a bit more subtle. We can use the rank factorization of A. Any matrix A of rank r can be factored as A = CR, where C is an n × r matrix of rank r, and R is an r × n matrix of rank r.
We want to find B such that ABA = A, or (CR)B(CR) = CR. If we can find a matrix B' such that RB'C = I (the r × r identity matrix), then we have (CR)B(CR) = C(RB'C)R = CIR = CR = A.
We can always find such a matrix B'. Since C has rank r, its columns are linearly independent, so C has a left inverse L such that LC = I. Since R has rank r, its rows are linearly independent, so R has a right inverse M such that RM = I. Then we can choose B' = MRCL. Then RB'C = RMRCLC = I*I = I.
Therefore, B = B' = MRCL is a matrix such that ABA = A.
In conclusion, such a matrix B always exists, regardless of whether A is invertible. When A is invertible, B is simply A⁻¹. When A is not invertible, a suitable B can be constructed by using the rank factorization of A.
Question 1185460: Table: Rate of the Cricket Chirps
Temperature in ℉
40
60
80
100
120
Rate
(Number of Chirps per Minute)
0
86
172
258
516
a.) Find a formula for g if g(t) represents the number of chirps per minute a cricket makes at temperature t degrees Fahrenheit.
b.) If f(c) represents the Fahrenheit reading that corresponds to a Celsius reading of c, which between the two functions g(f(t)) or f(g(t)) represents the number of chirps per minute a cricket makes when the temperature is c degrees Celsius?
c.) For the function in (b), write a formula for this and name it function h.
d.)Find the rate at which a cricket chirps if the temperature is __℉? __℃?
e.)Find the slope of the function g(t), h(c), and f(c). What does the slope of g(t) mean within the context of the problem?
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to solve this cricket chirp problem:
**(a) Formula for g(t):**
The data points suggest a linear relationship. Let's find the slope (m) and y-intercept (b) of the line.
1. **Choose two points:** Let's use (40, 0) and (60, 86).
2. **Calculate the slope (m):**
m = (change in y) / (change in x) = (86 - 0) / (60 - 40) = 86 / 20 = 4.3
3. **Find the y-intercept (b):** Use the point-slope form of a line (y - y₁ = m(x - x₁)) and one of the points, or plug one of the points into y=mx+b. Using (40,0):
0 = 4.3 * 40 + b
b = -172
4. **Write the equation:**
g(t) = 4.3t - 172
**(b) Which composite function represents chirps at Celsius temperature?**
* f(c) converts Celsius to Fahrenheit.
* g(t) converts Fahrenheit to chirps per minute.
Therefore, *g(f(c))* is the correct composite function. It first converts Celsius to Fahrenheit using f(c), and then converts the Fahrenheit temperature to chirps per minute using g(t).
**(c) Formula for h(c) = g(f(c)):**
1. **Formula for f(c):** The formula to convert Celsius to Fahrenheit is:
f(c) = (9/5)c + 32
2. **Substitute f(c) into g(t):**
h(c) = g(f(c)) = 4.3 * f(c) - 172
h(c) = 4.3 * ((9/5)c + 32) - 172
h(c) = (38.7/5)c + 137.6 - 172
h(c) = 7.74c - 34.4
**(d) Chirp rate at specific temperatures:**
You need to provide the specific temperatures (one in Fahrenheit and one in Celsius) to calculate the chirp rates. Plug the Fahrenheit temperature into g(t) and the Celsius temperature into h(c).
**(e) Slopes and their meaning:**
* **Slope of g(t):** The slope of g(t) is 4.3. This means that for every 1-degree Fahrenheit increase in temperature, the cricket chirp rate increases by 4.3 chirps per minute.
* **Slope of h(c):** The slope of h(c) is 7.74. This means that for every 1-degree Celsius increase in temperature, the cricket chirp rate increases by 7.74 chirps per minute.
* **Slope of f(c):** The slope of f(c) is 9/5 or 1.8. This means that for every 1-degree Celsius increase in temperature, the Fahrenheit temperature increases by 1.8 degrees.
Question 1186205: The Intellectual Company produces a chemical solution used for cleaning carpets. This chemical is made from a mixture of two other chemicals which contain cleaning agent X and cleaning agent Y. Their product must contain 175 units of agent X and 150 units of agent Y and weigh at least 100 pounds. Chemical A costs ₱ 8 per pound, while chemical B costs ₱ 6 per pound. Chemical A contains one unit of agent X and three units of agent Y. Chemical B contains seven units of agent X and one unit of agent Y.
a. Set up the following:
i. Variables
ii. Constraints
iii. Objective Function
b. Find the minimum cost
c. Determine the best combination of the ingredients to minimize the cost.
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52875)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The Intellectual Company produces a chemical solution used for cleaning carpets. This chemical is made from a mixture of two other chemicals which contain cleaning agent X and cleaning agent Y. Their product must contain 175 units of agent X and 150 units of agent Y and weigh at least 100 pounds. Chemical A costs ₱ 8 per pound, while chemical B costs ₱ 6 per pound. Chemical A contains one unit of agent X and three units of agent Y. Chemical B contains seven units of agent X and one unit of agent Y.
a. Set up the following:
i. Variables
ii. Constraints
iii. Objective Function
b. Find the minimum cost
c. Determine the best combination of the ingredients to minimize the cost.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution in the post by @CPhill, giving the answer
x = 43 pounds of chemical A and y = 19 pounds of chemical B
is INCORRECT. It can be easily disproved, since x + y = 43 + 19 = 62, which is less than 100.
Thus the restriction x+y >= 100 of the problem is not satisfied: it is FAILED, instead.
The cause is that @CPhill incorrectly determined the feasibility domain and used WRONG vertices for estimations.
Below is my solution, proper and correct.
**a. Set up:**
**i. Variables:**
* x = pounds of chemical A
* y = pounds of chemical B
**ii. Constraints:**
* Agent X: x + 7y ≥ 175
* Agent Y: 3x + y ≥ 150
* Weight: x + y ≥ 100
* Non-negativity: x ≥ 0, y ≥ 0
**iii. Objective Function:**
Minimize Cost (C) = 8x + 6y
**b. Find the minimum cost:**
1. **Graph the constraints:** Treat each inequality as an equation and plot the lines. Shade the appropriate region based on the inequality.
For example, for x + 7y ≥ 175, plot the line x + 7y = 175, and shade the region *above* and to the *right* of the lines.
Do this for all constraints.
2. **Identify the feasible region:** The feasible region is the area where all the shaded regions overlap.
3. **Find the vertices:** The vertices of the feasible region are the points where the constraint lines intersect.
Solve systems of equations to find these intersection points. The relevant vertices are:
* Intersection of x + 7y = 175 and y = 0: x = 175, y = 0
* Intersection of x + 7y = 175 and x + y = 100: Solving these gives x = 87.5, y = 12.5
* Intersection of 3x + y = 150 and x + y = 100: Solving these gives x = 25, y = 75
* Intersection of 3x + y = 175 and x = 0: Solving these gives x = 0, y = 175
4. **Evaluate the objective function at each vertex:**
* C(175, 0) = 8*175 + 6*0 = 1400
* C( 87.5, 12.5) = 8*81.5 + 6*12.5 = 727
* C(25, 75) = 8*25 + 6*75 = 650
* C(0, 175) = 8*0 + 6*175 = 1050
5. **Determine the minimum cost:** The minimum cost is the smallest value of the objective function.
The minimum cost is ₱650.
**c. Determine the best combination of ingredients:**
The best combination of ingredients is the (x, y) values that correspond to the minimum cost.
The minimum cost of ₱650 occurs when x = 25 and y = 75.
Therefore, the best combination is **25 pounds of chemical A and 75 pounds of chemical B**. <<<---=== ANSWER
Solved.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to set up and solve this linear programming problem:
**a. Set up:**
**i. Variables:**
* x = pounds of chemical A
* y = pounds of chemical B
**ii. Constraints:**
* Agent X: x + 7y ≥ 175
* Agent Y: 3x + y ≥ 150
* Weight: x + y ≥ 100
* Non-negativity: x ≥ 0, y ≥ 0
**iii. Objective Function:**
Minimize Cost (C) = 8x + 6y
**b. Find the minimum cost:**
1. **Graph the constraints:** Treat each inequality as an equation and plot the lines. Shade the appropriate region based on the inequality. For example, for x + 7y ≥ 175, plot the line x + 7y = 175, and shade the region *above* and to the *right* of the line. Do this for all constraints.
2. **Identify the feasible region:** The feasible region is the area where all the shaded regions overlap.
3. **Find the vertices:** The vertices of the feasible region are the points where the constraint lines intersect. Solve systems of equations to find these intersection points. The relevant vertices are:
* Intersection of x + 7y = 175 and 3x + y = 150: Solving these gives x = 43, y = 19
* Intersection of 3x + y = 150 and x + y = 100: Solving these gives x = 25, y = 75
* Intersection of x + 7y = 175 and x + y = 100: Solving these gives x = 12.5, y = 87.5
4. **Evaluate the objective function at each vertex:**
* C(43, 19) = 8(43) + 6(19) = 344 + 114 = ₱458
* C(25, 75) = 8(25) + 6(75) = 200 + 450 = ₱650
* C(12.5, 87.5) = 8(12.5) + 6(87.5) = 100 + 525 = ₱625
5. **Determine the minimum cost:** The minimum cost is the smallest value of the objective function.
The minimum cost is ₱458.
**c. Determine the best combination of ingredients:**
The best combination of ingredients is the (x, y) values that correspond to the minimum cost.
The minimum cost of ₱458 occurs when x = 43 and y = 19.
Therefore, the best combination is **43 pounds of chemical A and 19 pounds of chemical B**.
Question 1186248: The Intellectual Company produces a chemical solution used for cleaning carpets. This chemical is made from a mixture of two other chemicals which contain cleaning agent X and cleaning agent Y. Their product must contain 175 units of agent X and 150 units of agent Y and weigh at least 100 pounds. Chemical A costs ₱ 8 per pound, while chemical B costs ₱ 6 per pound. Chemical A contains one unit of agent X and three units of agent Y. Chemical B contains seven units of agent X and one unit of agent Y.
a. Set up the following:
i. Variables
ii. Constraints
iii. Objective Function
b. Find the minimum cost
c. Determine the best combination of the ingredients to minimize the cost.
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52875)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The Intellectual Company produces a chemical solution used for cleaning carpets.
This chemical is made from a mixture of two other chemicals which contain cleaning agent X and cleaning agent Y.
Their product must contain 175 units of agent X and 150 units of agent Y and weigh at least 100 pounds.
Chemical A costs ₱ 8 per pound, while chemical B costs ₱ 6 per pound.
Chemical A contains one unit of agent X and three units of agent Y.
Chemical B contains seven units of agent X and one unit of agent Y.
a. Set up the following:
i. Variables
ii. Constraints
iii. Objective Function
b. Find the minimum cost
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution in the post by @CPhill, giving the answer
x = 43 pounds of chemical A and y = 19 pounds of chemical B
is INCORRECT. It can be easily disproved, since x + y = 43 + 19 = 62, which is less than 100.
Thus the restriction x+y >= 100 of the problem is not satisfied: it is FAILED, instead.
The cause is that @CPhill incorrectly determined the feasibility domain and used WRONG vertices for estimations.
Below is my solution, proper and correct.
**a. Set up:**
**i. Variables:**
* x = pounds of chemical A
* y = pounds of chemical B
**ii. Constraints:**
* Agent X: x + 7y ≥ 175
* Agent Y: 3x + y ≥ 150
* Weight: x + y ≥ 100
* Non-negativity: x ≥ 0, y ≥ 0
**iii. Objective Function:**
Minimize Cost (C) = 8x + 6y
**b. Find the minimum cost:**
1. **Graph the constraints:** Treat each inequality as an equation and plot the lines. Shade the appropriate region based on the inequality.
For example, for x + 7y ≥ 175, plot the line x + 7y = 175, and shade the region *above* and to the *right* of the lines.
Do this for all constraints.
2. **Identify the feasible region:** The feasible region is the area where all the shaded regions overlap.
3. **Find the vertices:** The vertices of the feasible region are the points where the constraint lines intersect.
Solve systems of equations to find these intersection points. The relevant vertices are:
* Intersection of x + 7y = 175 and y = 0: x = 175, y = 0
* Intersection of x + 7y = 175 and x + y = 100: Solving these gives x = 87.5, y = 12.5
* Intersection of 3x + y = 150 and x + y = 100: Solving these gives x = 25, y = 75
* Intersection of 3x + y = 175 and x = 0: Solving these gives x = 0, y = 175
4. **Evaluate the objective function at each vertex:**
* C(175, 0) = 8*175 + 6*0 = 1400
* C( 87.5, 12.5) = 8*81.5 + 6*12.5 = 727
* C(25, 75) = 8*25 + 6*75 = 650
* C(0, 175) = 8*0 + 6*175 = 1050
5. **Determine the minimum cost:** The minimum cost is the smallest value of the objective function.
The minimum cost is ₱650.
**c. Determine the best combination of ingredients:**
The best combination of ingredients is the (x, y) values that correspond to the minimum cost.
The minimum cost of ₱650 occurs when x = 25 and y = 75.
Therefore, the best combination is **25 pounds of chemical A and 75 pounds of chemical B**. <<<---=== ANSWER
Solved.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to set up and solve this linear programming problem:
**a. Set up:**
**i. Variables:**
* x = pounds of chemical A
* y = pounds of chemical B
**ii. Constraints:**
* Agent X: 1x + 7y >= 175
* Agent Y: 3x + 1y >= 150
* Weight: x + y >= 100
* Non-negativity: x >= 0, y >= 0 (We can't have negative amounts of chemicals.)
**iii. Objective Function:**
We want to minimize the cost, which is given by:
Cost (C) = 8x + 6y
**b. Find the minimum cost:**
To find the minimum cost, we need to graph the constraints and find the feasible region. The optimal solution will occur at one of the vertices (corners) of the feasible region.
1. **Graph the constraints:** Treat each inequality as an equation and plot the lines. Then shade the appropriate region based on the inequality.
* x + 7y = 175
* 3x + y = 150
* x + y = 100
2. **Identify the feasible region:** The feasible region is the area where all the shaded regions overlap.
3. **Find the vertices:** The vertices of the feasible region are the points where the constraint lines intersect. You'll need to solve systems of equations to find these intersection points. The relevant vertices are usually where two constraints intersect.
* Intersection of x + 7y = 175 and 3x + y = 150: Solving these equations gives x = 43, y = 19
* Intersection of 3x + y = 150 and x + y = 100: Solving these equations gives x = 25, y = 75
* Intersection of x + 7y = 175 and x + y = 100: Solving these equations gives x = 75/6 = 12.5, y = 87.5
4. **Evaluate the objective function at each vertex:**
* C(43, 19) = 8(43) + 6(19) = 344 + 114 = 458
* C(25, 75) = 8(25) + 6(75) = 200 + 450 = 650
* C(12.5, 87.5) = 8(12.5) + 6(87.5) = 100 + 525 = 625
5. **Determine the minimum cost:** The minimum cost is the smallest value of the objective function at the vertices.
The minimum cost is ₱458.
**c. Determine the best combination of ingredients:**
The best combination of ingredients is the (x, y) values that correspond to the minimum cost.
The minimum cost of ₱458 occurs when x = 43 and y = 19.
Therefore, the best combination is 43 pounds of chemical A and 19 pounds of chemical B.
Question 1186463: To greet the 2020 SHS graduates, a tarpaulin is to be set along the national highway. If the area of the tarp is to be 35/4 m^2 and its perimeter 27/2 meters, what should be the dimensions of the tarpaulin
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to find the dimensions of the tarpaulin:
**1. Set up the equations:**
Let 'w' be the width and 'h' be the height of the tarpaulin. We are given the area and the perimeter:
* Area: w * h = 35/4
* Perimeter: 2w + 2h = 27/2
**2. Solve for one variable in terms of the other:**
From the area equation, we can express h in terms of w:
h = (35/4) / w
**3. Substitute into the perimeter equation:**
2w + 2 * ((35/4) / w) = 27/2
**4. Simplify and solve for w:**
2w + (35/2w) = 27/2
Multiply the entire equation by 2w to get rid of the fraction:
4w² + 35 = 27w
4w² - 27w + 35 = 0
**5. Solve the quadratic equation:**
We can use the quadratic formula to solve for w. The formula is:
w = (-b ± sqrt(b² - 4ac)) / 2a
In our equation, a = 4, b = -27, and c = 35.
w = (27 ± sqrt((-27)² - 4 * 4 * 35)) / (2 * 4)
w = (27 ± sqrt(729 - 560)) / 8
w = (27 ± sqrt(169)) / 8
w = (27 ± 13) / 8
This gives us two possible solutions for w:
w = (27 + 13) / 8 = 40 / 8 = 5
w = (27 - 13) / 8 = 14 / 8 = 7/4 = 1.75
**6. Find the corresponding values for h:**
If w = 5, then h = (35/4) / 5 = 35/20 = 7/4 = 1.75
If w = 1.75, then h = (35/4) / 1.75 = 5
**7. State the dimensions:**
The dimensions of the tarpaulin are 5 meters by 1.75 meters. It doesn't matter which dimension is width or height.
Question 1191317: Determine whether the relation R on the set of all real numbers is reflective, symmetric, and/or transitive, where open parentheses x comma y close parentheses element of R if and only if x y greater or equal than 0. Is the relation R an equivalence relation?
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's analyze the relation R defined on the set of real numbers, where (x, y) ∈ R if and only if xy ≥ 0.
* **Reflexive:** A relation is reflexive if for all x, (x, x) ∈ R. In our case, this means x*x = x² ≥ 0. Since the square of any real number is non-negative, this condition is always true. Therefore, R *is* reflexive.
* **Symmetric:** A relation is symmetric if for all x and y, if (x, y) ∈ R, then (y, x) ∈ R. If xy ≥ 0, then yx ≥ 0 (since multiplication is commutative). So, if (x, y) ∈ R, then (y, x) ∈ R. Therefore, R *is* symmetric.
* **Transitive:** A relation is transitive if for all x, y, and z, if (x, y) ∈ R and (y, z) ∈ R, then (x, z) ∈ R. Let's consider a counterexample:
* Let x = -1, y = 0, and z = 1.
* x*y = (-1)*0 = 0 ≥ 0, so (x, y) ∈ R.
* y*z = 0*1 = 0 ≥ 0, so (y, z) ∈ R.
* x*z = (-1)*1 = -1 < 0, so (x, z) ∉ R.
Since we found a case where (x, y) and (y, z) are in R, but (x, z) is not, R is *not* transitive.
* **Equivalence Relation:** A relation is an equivalence relation if it is reflexive, symmetric, *and* transitive. Since R is not transitive, R is *not* an equivalence relation.
**In summary:**
* R is reflexive.
* R is symmetric.
* R is *not* transitive.
* R is *not* an equivalence relation.
Question 1192134: Use a k-map to simplify the following function:
F(W, X, Y, Z) = X'Y' + XYZ' + WXY + W'X'Y' + WZ
Can I get an explanation of this homework question step-by-step please? Thank you very much!!!
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to simplify the function F(W, X, Y, Z) = X'Y' + XYZ' + WXY + W'X'Y' + WZ using a K-map:
1. **Set up the K-map:**
```
WZ
00 01 11 10
WX 00 1 1 1 1 (X'Y')
01 0 0 1 0 (XYZ')
11 0 1 1 0 (WXY)
10 1 1 1 1 (W'X'Y' and WZ)
```
2. **Fill in the K-map:**
* X'Y' (W=0, X=0, Y=0): This covers the first row (00) entirely, regardless of Z.
* XYZ' (X=1, Y=1, Z=0): This is the cell at WX=01, YZ=10.
* WXY (W=1, X=1, Y=1): This is the cell at WX=11, YZ=11.
* W'X'Y' (W=0, X=0, Y=0): This is already covered by X'Y'.
* WZ: This term covers all cells where W=1 *or* Z=1. The cells where W=1 are already covered by WXY and a portion of X'Y'. The cells where Z=1 are on the 01 and 11 columns.
3. **Group the 1s:** We want to make the largest possible groups of 1s, where the groups are powers of 2 (1, 2, 4, 8, 16).
* **Group 1:** The entire first row (X'Y') is a group of 4. This represents X'Y'.
* **Group 2:** The 1s in the bottom row (W=1) are best grouped as a group of 4 (covering WZ). This represents W.
* **Group 3:** The remaining '1' at WX=01 and YZ=10 is covered by XYZ'.
4. **Write the simplified expression:**
By combining the groups, we get the simplified Boolean expression:
F(W, X, Y, Z) = X'Y' + W + XYZ'
Therefore, the simplified function is **F(W, X, Y, Z) = X'Y' + W + XYZ'**.
Question 1192375: 42 Marijuana Usage among High School Students Figure 2.14 illustrates some sur vey data regarding the usage of marijuana among high school students. A sample of high werpen (ca school students was taken every 2 years between 1979 and 1989. The data in Figure 2.14 what reflects the percentage of students surveyed who indicated they had used marijuana during the previous 30 days. The data points suggest that the percentage of students having used marijuana is decreasing at an approximately linear rate over time. If the data points for 1979 (1, 36.5) and 1989 (11, 16.5) are used to estimate the linear equation which relates the percentage of students P to time t (t = 1 corresponding to 1979): (a) Determine the slope-intercept form of the estimating equation. (b) Forecast the expected percentage for 1991 and 1995. (c) Interpret the meaning of the slope and P intercept. word problem
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website!
**1. Find the Slope**
* **Slope (m):** (Change in P) / (Change in t) = (16.5 - 36.5) / (11 - 1) = -20 / 10 = -2
**2. Find the Y-intercept (b)**
* **Use the point-slope form:** P - P1 = m(t - t1)
* Use the point (1, 36.5) and the slope (-2)
* P - 36.5 = -2(t - 1)
* P - 36.5 = -2t + 2
* P = -2t + 38.5
**a) Slope-Intercept Form of the Estimating Equation:**
* **P = -2t + 38.5**
* where:
* P is the percentage of students using marijuana
* t is the time in years since 1978 (t = 1 corresponds to 1979)
**b) Forecast the Expected Percentage**
* **1991:**
* t = 1991 - 1978 = 13
* P = -2(13) + 38.5 = 12.5%
* **1995:**
* t = 1995 - 1978 = 17
* P = -2(17) + 38.5 = 4.5%
**c) Interpretation**
* **Slope:** The slope of -2 indicates that the percentage of students using marijuana is estimated to decrease by 2% per year.
* **P-intercept (38.5):** This represents the estimated percentage of students using marijuana in 1978 (when t = 0). However, since the model is based on data from 1979 onwards, this intercept may not have a practical interpretation in this specific context.
**Note:**
* This linear model provides an estimation based on the given data.
* Actual trends may not perfectly follow this linear pattern.
* Other factors could influence marijuana usage among high school students, and this model may not capture all of these factors.
**a) Determine the slope-intercept form of the estimating equation.**
* **Given Data Points:**
* (t1, P1) = (1, 36.5)
* (t2, P2) = (11, 16.5)
* **Calculate Slope (m):**
* m = (P2 - P1) / (t2 - t1)
* m = (16.5 - 36.5) / (11 - 1)
* m = -20 / 10
* m = -2
* **Calculate y-intercept (b):**
* Use the point-slope form: P - P1 = m(t - t1)
* P - 36.5 = -2(t - 1)
* P - 36.5 = -2t + 2
* P = -2t + 38.5
* **Slope-intercept form:**
* **P = -2t + 38.5**
**b) Forecast the expected percentage for 1991 and 1995.**
* **For 1991 (t = 13):**
* P = -2(13) + 38.5
* P = -26 + 38.5
* P = 12.5%
* **For 1995 (t = 17):**
* P = -2(17) + 38.5
* P = -34 + 38.5
* P = 4.5%
**c) Interpret the meaning of the slope and P intercept.**
* **Slope (-2):**
* The slope represents the rate of change in the percentage of students using marijuana per year.
* In this case, it indicates that the percentage of students using marijuana is decreasing by 2% per year.
* **P-intercept (38.5):**
* The P-intercept represents the estimated percentage of students using marijuana in the base year (1979, when t = 1).
* It suggests that in 1979, approximately 38.5% of high school students used marijuana.
**Note:**
* This model is based on a linear assumption and may not accurately predict future trends.
* Factors other than time can influence marijuana usage among high school students.
I hope this helps! Let me know if you have any further questions.
Question 1194124: Hi, i don't really know what to do here.
The linear operator A is called the idempotent or the projection operator if A^2 = A. What is the canonical operator of the idempotent operator Jordan?
in shape?
Answer by parmen(42)  (Show Source): (Show Source):
You can put this solution on YOUR website! **Key Properties of Idempotent Operators:**
* **Definition:** An operator A is idempotent if A² = A.
* **Eigenvalues:** The only possible eigenvalues of an idempotent operator are 0 and 1.
* **Diagonalizability:** Idempotent operators are always diagonalizable.
**Canonical Form of an Idempotent Operator:**
The canonical form of an idempotent operator is a diagonal matrix with only 0s and 1s on the diagonal.
**Explanation:**
* **Diagonalization:** Since idempotent operators are diagonalizable, there exists an invertible matrix P such that:
P⁻¹AP = D
where D is a diagonal matrix.
* **Eigenvalues and Diagonal:**
- The diagonal entries of D represent the eigenvalues of A.
- Since the only eigenvalues of an idempotent operator are 0 and 1, the diagonal of D will consist of only 0s and 1s.
**Example:**
Let A be an idempotent operator. Its canonical form (Jordan form) would be:
```
D =
| 1 0 0 0 |
| 0 1 0 0 |
| 0 0 0 0 |
| 0 0 0 0 |
```
This represents a 4x4 matrix with two eigenvalues: 1 (with multiplicity 2) and 0 (with multiplicity 2).
**In Summary:**
The canonical form of an idempotent operator is a diagonal matrix with only 0s and 1s on the diagonal, reflecting its eigenvalues and its diagonalizability.
Question 1194381: Given the following function in two variables x and y
f(x, y) = x^3y+2x^4+y^5
a. Find the Jacobean determinant at point P (3,2)
b. Find the Hessian determinant at point P (1,3)
Answer by parmen(42)  (Show Source): (Show Source):
You can put this solution on YOUR website! **a. Find the Jacobian Determinant at point P (3, 2)**
1. **Calculate Partial Derivatives:**
- ∂f/∂x = 3x²y + 8x³
- ∂f/∂y = x³ + 5y⁴
2. **Evaluate Partial Derivatives at P (3, 2):**
- ∂f/∂x(3, 2) = 3(3)²(2) + 8(3)³ = 54 + 216 = 270
- ∂f/∂y(3, 2) = (3)³ + 5(2)⁴ = 27 + 80 = 107
3. **Construct the Jacobian Matrix:**
- The Jacobian matrix is a 1x2 matrix:
[ ∂f/∂x ∂f/∂y ]
[ 270 107 ]
4. **Calculate the Jacobian Determinant:**
- Since it's a 1x2 matrix, the determinant is not defined. The Jacobian determinant is only defined for square matrices (where the number of rows equals the number of columns).
**b. Find the Hessian Determinant at point P (1, 3)**
1. **Calculate Second-Order Partial Derivatives:**
- ∂²f/∂x² = 6xy + 24x²
- ∂²f/∂y² = 20y³
- ∂²f/∂x∂y = 3x²
- ∂²f/∂y∂x = 3x²
2. **Evaluate Second-Order Partial Derivatives at P (1, 3):**
- ∂²f/∂x²(1, 3) = 6(1)(3) + 24(1)² = 18 + 24 = 42
- ∂²f/∂y²(1, 3) = 20(3)³ = 540
- ∂²f/∂x∂y(1, 3) = 3(1)² = 3
- ∂²f/∂y∂x(1, 3) = 3(1)² = 3
3. **Construct the Hessian Matrix:**
- The Hessian matrix is a 2x2 matrix:
[ ∂²f/∂x² ∂²f/∂x∂y ]
[ ∂²f/∂y∂x ∂²f/∂y² ]
[ 42 3 ]
[ 3 540 ]
4. **Calculate the Hessian Determinant:**
- det(Hessian) = (42)(540) - (3)(3) = 22680 - 9 = 22671
**Therefore:**
* The Jacobian determinant at point P (3, 2) is not defined.
* The Hessian determinant at point P (1, 3) is 22671.
Question 1194394: Given the following quadratic form involving three variables,
Q (x_1, x_2, x_3) = 5(x^2)_1 + 8(x^1)(x^3) + 3(x^2)_2 - 6(x^2)(x^3) + 10(x^2)_3
a. Derive the symmetric matrix associated with Q
b. Determine the definiteness of the matrix you derived in a
Answer by parmen(42)  (Show Source): (Show Source):
You can put this solution on YOUR website! **a. Derive the Symmetric Matrix Associated with Q**
1. **Organize Terms:**
- Rearrange the given quadratic form to group terms involving the same variables:
Q(x₁, x₂, x₃) = 5x₁² + 3x₂² + 10x₃² + 8x₁x₃ - 6x₂x₃
2. **Identify Coefficients:**
- Extract the coefficients of the quadratic terms, linear terms, and cross-product terms:
- Coefficient of x₁²: 5
- Coefficient of x₂²: 3
- Coefficient of x₃²: 10
- Coefficient of x₁x₃: 8 (note: this is the coefficient of both x₁x₃ and x₃x₁)
- Coefficient of x₂x₃: -6 (note: this is the coefficient of both x₂x₃ and x₃x₂)
3. **Construct the Symmetric Matrix:**
- Arrange the coefficients into a symmetric matrix:
A = | 5 0 4 |
| 0 3 -3 |
| 4 -3 10 |
- This matrix is symmetric because the coefficients of the cross-product terms (x₁x₃ and x₂x₃) are placed symmetrically off the main diagonal.
**b. Determine the Definiteness of the Matrix**
To determine the definiteness of the matrix A, we can use the following methods:
1. **Eigenvalue Method:**
- Calculate the eigenvalues of matrix A.
- If all eigenvalues are positive, the matrix is positive definite.
- If all eigenvalues are negative, the matrix is negative definite.
- If some eigenvalues are positive and some are negative, the matrix is indefinite.
- If some eigenvalues are zero and the rest are positive, the matrix is positive semidefinite.
- If some eigenvalues are zero and the rest are negative, the matrix is negative semidefinite.
2. **Leading Principal Minors Method:**
- Calculate the determinants of the leading principal minors of matrix A.
- If all leading principal minors are positive, the matrix is positive definite.
- If the signs of the leading principal minors alternate between positive and negative (starting with negative), the matrix is negative definite.
- If any leading principal minor is zero, the matrix is not definite.
**In this case, it's recommended to use a computational tool (like MATLAB, Python with NumPy/SciPy) to efficiently calculate eigenvalues and determinants for larger matrices.**
**Note:** The definiteness of the matrix A directly relates to the nature of the quadratic form Q(x₁, x₂, x₃). If A is positive definite, Q(x₁, x₂, x₃) will always be positive for any non-zero vector (x₁, x₂, x₃). Similarly, if A is negative definite, Q(x₁, x₂, x₃) will always be negative for any non-zero vector.
I hope this comprehensive explanation helps!
Question 1194421: If 0.3 units of output of the second industry is used to produce a unit output of the first industry, the correct form of this inter industry linkages can be expressed by
Answer by amarjeeth123(570)  (Show Source): (Show Source):
Question 1198270: Weather Service releases weather balloons twice daily at over 90 locations in the United States in order to collect data for meteorologists. The height h (in feet) of a balloon is a function of the time t (in seconds) after the balloon is released, as shown.
a. Making a Table Make a table showing the height of
a balloon after t seconds for t = 0 through t = 10.
b. Drawing a Graph A balloon bursts after a flight of about 7200 seconds. Graph the function and identify the domain and range.
Answer by proyaop(69)  (Show Source): (Show Source):
You can put this solution on YOUR website! **a. Making a Table**
Unfortunately, I cannot provide the exact height function (h(t)) for a weather balloon. The ascent rate varies depending on factors like balloon size, weight of the payload, atmospheric conditions (temperature, pressure, wind), and the type of gas used to inflate the balloon.
However, I can provide a hypothetical example of a simplified height function and create a table based on that:
**Simplified Height Function (Example):**
* Let's assume the balloon ascends at a constant rate of 5 meters per second.
* h(t) = 5t
**Table of Heights (Example):**
| Time (t) (seconds) | Height (h) (meters) |
|---|---|
| 0 | 0 |
| 1 | 5 |
| 2 | 10 |
| 3 | 15 |
| 4 | 20 |
| 5 | 25 |
| 6 | 30 |
| 7 | 35 |
| 8 | 40 |
| 9 | 45 |
| 10 | 50 |
**b. Drawing a Graph**
* **Based on the Example:**
* The graph of h(t) = 5t would be a straight line passing through the origin with a slope of 5.
* **Considering a Real-World Scenario:**
* The actual height of a weather balloon would likely not increase linearly. It would likely accelerate initially and then slow down as it reaches higher altitudes where the air density decreases.
* The graph would probably be a curve, possibly with an initial steeper slope and then gradually leveling off.
* **Domain and Range:**
* **Domain:**
* The domain represents the possible values for time (t).
* In this case, the domain is 0 ≤ t ≤ 7200 seconds (since the balloon bursts after 7200 seconds).
* **Range:**
* The range represents the possible values for height (h).
* In the simplified example, the range would depend on the maximum height reached.
**Important Notes:**
* This is a simplified example. The actual ascent rate of a weather balloon is much more complex.
* Weather balloon data is collected and analyzed by meteorological agencies. You can find more information and potentially access real-world data on their websites.
I hope this helps! Let me know if you have any further questions or would like to explore a more realistic height function.
Question 1200083: Let A be the matrix of coefficients of a 5 × 7 system of linear equations, A⃗x = ⃗b. Using row operations, you find that A is row equivalent to a matrix in reduced row echelon form with one row of zeroes at the bottom.
(a) What is rank(A)?
(b) How many free variables does the system have?
(c) For the given system how many possible solutions could it have? (Circle all which apply)
1. 0 solutions
2. 1 solution
3. infinite solutions
(d) For the associated homogeneous system A⃗x = ⃗0, how many possible solutions could it have? (Circle all which apply)
1. 0 solutions
2. 1 solution
3. infinite solutions
Answer by GingerAle(43)  (Show Source): (Show Source):
You can put this solution on YOUR website! **a) Rank(A)**
* The rank of a matrix is the number of non-zero rows in its row-echelon form.
* Since A has one row of zeros and is row equivalent to a matrix in reduced row echelon form, its rank is 4.
**b) Number of Free Variables**
* The number of free variables is equal to the number of columns minus the rank of the matrix.
* Number of free variables = 7 (columns) - 4 (rank) = 3
**c) Possible Solutions for A⃗x = ⃗b**
* **Possible Solutions:**
* **Infinite solutions**
* **No solutions**
* **Explanation:**
* If the last row in the reduced row echelon form of the augmented matrix [A | ⃗b] is of the form [0 0 0 | c] where c is a non-zero constant, then the system has no solution.
* Otherwise, if the last row is all zeros, the system will have infinite solutions due to the free variables.
**d) Possible Solutions for A⃗x = ⃗0**
* **Possible Solutions:**
* **Infinite solutions**
* **Explanation:**
* For the homogeneous system A⃗x = ⃗0, the last row in the augmented matrix [A | ⃗0] will always be all zeros.
* Since there are free variables, the homogeneous system will always have infinite solutions (including the trivial solution ⃗x = ⃗0).
**In Summary:**
* **Rank(A) = 4**
* **Number of Free Variables = 3**
* **Possible Solutions for A⃗x = ⃗b:** Infinite solutions or no solutions
* **Possible Solutions for A⃗x = ⃗0:** Infinite solutions
Question 1206684: Hello, I need help with the following problem:
Three basis are given in the plane. With respect to those basis a point has as components (x1,x2), (y1,y2) and (z1,z2). Suppose that [y1 y2] = [x1 x2]A, [z1 z2] = [x1 x2]B and [z1 z2] = [y1 y2]C being A,B,C 2x2 matrices. Express C as a function of A and B.
I very much appreciate your help.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! We're given the following relationships:
1. [y1 y2] = [x1 x2]A
2. [z1 z2] = [x1 x2]B
3. [z1 z2] = [y1 y2]C
We want to express C as a function of A and B.
**Step 1: Substitute [y1 y2] in equation 3:**
From equation 1, we know that [y1 y2] = [x1 x2]A. Substitute this into equation 3:
[z1 z2] = ([x1 x2]A)C
**Step 2: Substitute [z1 z2] from equation 2:**
From equation 2, we know that [z1 z2] = [x1 x2]B. Substitute this into the previous equation:
[x1 x2]B = ([x1 x2]A)C
**Step 3: Simplify and Solve for C:**
Since [x1 x2] is a common factor on both sides, we can cancel it out:
B = AC
**Now, to isolate C, we can multiply both sides by the inverse of A (assuming A is invertible):**
A⁻¹B = C
**Therefore, C = A⁻¹B.**
Question 1205507: If TA is multiplication by a matrix A with three columns, then the kernel of TA is one of four possible geometric objects. What are they? Explain how you reached your conclusion
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Understanding the Kernel
The kernel of a linear transformation, in this case, the linear transformation induced by matrix A, is the set of all vectors that, when multiplied by A, result in the zero vector. Geometrically, it represents the subspace of the domain that is mapped to the origin of the codomain.
Possible Geometric Interpretations
Given that A is a 3x3 matrix, the domain of TA is R³. The kernel of TA can be:
A Point:
This occurs when the kernel only contains the zero vector. Geometrically, this is a single point in R³.
Algebraically, the matrix A must have full rank, meaning its columns are linearly independent.
A Line:
This occurs when the kernel is one-dimensional. It's a line passing through the origin in R³.
Algebraically, the matrix A must have rank 2, meaning two of its columns are linearly independent.
A Plane:
This occurs when the kernel is two-dimensional. It's a plane passing through the origin in R³.
Algebraically, the matrix A must have rank 1, meaning only one of its columns is linearly independent.
All of R³:
This occurs when the kernel is three-dimensional. Every vector in R³ is mapped to the zero vector.
Algebraically, the matrix A must be the zero matrix.
Conclusion
The kernel of a linear transformation induced by a 3x3 matrix can be interpreted geometrically as one of the following: a point, a line, a plane, or the entire space R³. The specific geometric interpretation depends on the rank of the matrix A, which determines the dimension of the kernel.
Question 1208221: A stadium has 50,000 seats. Seats sell for $35 in Section A, $20 in Section B, and $15 in Section C.
The number of seats in Section A equals the total number of seats in Sections B and C.
Suppose the stadium takes in $1,323,000 from each sold-out event. How many seats does each section hold?
Answer by ikleyn(52875)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A stadium has 50,000 seats. Seats sell for $35 in Section A, $20 in Section B, and $15 in Section C.
The number of seats in Section A equals the total number of seats in Sections B and C.
Suppose the stadium takes in $1,323,000 from each sold-out event. How many seats does each section hold?
~~~~~~~~~~~~~~~~~~~~
We assume that all tickets are sold and the amount $1,323,000 relates to 50,000 sold tickets.
Since "the number of seats in Section A equals the total number of seats in Sections B and C<
it means that the number of seats in section A is half of the total 50,000 seats, i.e. 25,000 seats,
while the total number of seats in sections B and C is another half of the total 50,000 seats,
i.e. 25.000 seats.
Thus, part of the problem is just solved: we derived that section A has 25,000 seats.
From it, we conclude that the cost of tickets sold in sections B and C is
1323000 - 25000*35 = 448000 dollars.
Thus we know that total number of seats in sections B and C is 25,000 and the total cost of tickets
sold in these section B and C is 448000 dollars.
Let x be the number of seats in section B. Then the number of seats in section C is 25000-x.
Having it, write an equation for the total cost of tickets in sections B and C
20x + 15(25000-x) = 448000.
Simplify and find x
20x + 15*25000 - 15x = 448000
20x - 15x = 448000 - 15*25000
5x = 73000
x = 73000/5 = 14600.
ANSWER. There are 25000 seats in section A; 14600 seats in section B and 25000-14600 = 10400 seats in section C.
CHECK. The total cost of all tickets is 35*25000 + 20*14600 + 15*10400 = 1,323000 dollars.
It coincides with the given value. Hence, the solution is correct.
Solved.
Question 1206490: 5x+y=-13 and -x2y=-10 solve by substitution
Answer by josgarithmetic(39629)  (Show Source): (Show Source):
Question 1206083: if z=x-8/2x, what is x
Answer by greenestamps(13208)   (Show Source): (Show Source):
Question 1205886: Use the pair of functions to find f(g(x))
and g(f(x))
. Simplify your answers.
f(x)=sqrt(x)+8,g(x)=x^2+3
f(g(x))=
g(f(x))=
Found 2 solutions by Theo, MathLover1:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! f(x) = sqrt(x) + 8
g(x) = x^2 + 3
to find f(g(x)), replace x in f(x) with g(x) to get:
f(g(x)) = sqrt(g(x)) + 8
since g(x) = x^2 + 3, you get:
f(g(x)) = sqrt(x^2 + 3) + 8
when x = 3, you get:
f(g(x)) = sqrt(3^2 + 3) + 8 = 11.46410162
this is equivalent to finding g(x) first and then finding f(g(x)).
g(x) = x^2 + 3.
when x = 3, g(x) = 3^2 + 3 = 12.
f(g(x)) becomes f(12) = sqrt(12) + 8 = 11.46410162.
f(x) and g(x) are repeated here to make them easier to reference.
f(x) = sqrt(x) + 8
g(x) = x^2 + 3
to find g(f(x)), replace x in g(x) with f(x) to get:
g(f(x)) = f(x)^2 + 3
since f(x) = sqrt(x) + 8, you get:
g(f(x)) = (sqrt(x) + 8)^2 + 3
when x = 3, you get:
g(f(x)) = (sqrt(3) + 8)^2 + 3 = 97.71281292.
this is equivalent to finding f(x) first and then finding g(f(x)).
f(x) = sqrt(x) + 8
when x = 3, f(x) = sqrt(3) + 8 = 9.732050808.
g(f(x)) becomes g(9.732050808) = 9.732050808^2 + 3 = 97.71281292.
your solution is:
f(g(x)) = sqrt(x^2 + 3) + 8
g(f(x)) = (sqrt(x) + 8)^2 + 3
here's a reference on composite functions.
https://www.youtube.com/watch?v=QXGQtkbyFTs
there are more videos on youtube regarding composition of functions, so feel free to look for others if looking at one is insufficient.
this particular tutor is pretty good as far as i can tell.
Answer by MathLover1(20850)   (Show Source): (Show Source):
Question 1205327: An individual needs a daily supplement of at least 510 units of vitamin C and 266 of vitamin E and agrees to obtain this supplement by eating two foods, I and II. Each ounce of food I contains 102 units of vitamin C and 19 units of vitamin E, while each ounce of food II contains 51 units of vitamin C and also 38 units of vitamin E. The total supplement of these two foods must be at most 21 ounces. Unfortunately, food I contains 19 units of cholesterol per ounce and food II contains 13 units of cholesterol per ounce. Find the appropriate amounts of the two food supplements so that cholesterol is minimized. Find the minimum amount of cholesterol.
amount of food I
amount of food II
minimum cholesterol
Answer by ikleyn(52875)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
An individual needs a daily supplement of at least 510 units of vitamin C and 266 of vitamin E
and agrees to obtain this supplement by eating two foods, I and II.
Each ounce of food I contains 102 units of vitamin C and 19 units of vitamin E, while
each ounce of food II contains 51 units of vitamin C and also 38 units of vitamin E.
The total supplement of these two foods must be at most 21 ounces.
Unfortunately, food I contains 19 units of cholesterol per ounce and food II contains 13 units of cholesterol per ounce.
Find the appropriate amounts of the two food supplements so that cholesterol is minimized. Find the minimum amount of cholesterol.
amount of food I
amount of food II
minimum cholesterol
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution by @Theo is incorrect.
It is incorrect, because Theo incorrectly treats the condition
"The total supplement of these two foods must be at most 21 ounces."
Theo writes for it
x + y >= 21
in his basic restrictions, while the correct treatment is
x + y <= 21 ("at most").
The solution by @math_tutor2020 is correct.
The only essential note to the @math_tutor2020 solution is that the dashed lines
in his plot DO BELONG to the solution region.
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085, 5086..5130, 5131..5175, 5176..5220, 5221..5265, 5266..5310, 5311..5355, 5356..5400, 5401..5445, 5446..5490, 5491..5535, 5536..5580, 5581..5625, 5626..5670, 5671..5715, 5716..5760
|






