SOLUTION: Let x and y be integers. If x and y satisfy 37x + 82y = -172 and x + y = -1, then find x.

                    Solve by the Elimination method


Starting equations are

    37x + 82y  = -172,       (1)

      x +   y  =   -1.       (2)


They want you find x.  So, let's exclude y from the equations.
For it, multiply equation (2) by 82. Keep equation (1) as is

    37x + 82y  = -172,       (1')

    82x + 82y =   -82.       (2')


Now subtract equation (1') from equation (2').  The terms with "y" will cancel each other, 
and you will get

    82x - 37x = -82 - (-172),

or
         45x      =      90.


Hence, x = 90/45 = 2.


At this point, we formally completed the solution.


But we still need to check that the other solution, "y", is the integer number.

For it we substitute x= 2 into equation (2) and find

    y = -1 - x = -1 - 2 = -3.


Both "x" and "y" are integer, so, all the requirements are satisfied, and the  ANSWER  is  x= 2.



                    Solve by the Substitution method


From equation (2), express y = -1 - x and substitute it into equation (1).  You will get

    37x + 82*(-1-x)  = -172,

    37x - 82 - 82x     = -172,

     37x - 82x = -172 + 82

          -45x      =    -90

                x  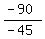    =  = 2.


We get the same answer.