SOLUTION: A manufacturer makes 2-minute, 6-minute, and 9-minute film developers. Each ton of 2-minute developer requires 6 minutes in plant A and 24 mmutes in plant B. Each ton of 6-minute d

Let x = tons of the 2-minute developer produced,

    y = tons of the 6-minute developer produced,

    z = tons of the 9-minute developer produced.


Then time needed at plant A is   6x + 12y + 12z minutes.

     Time needed at plant B is  24x + 12y + 12z minutes.


Equations for fully used regime

     6x + 12y + 12z = 600  minutes,   (1)

    24x + 12y + 12z = 960  minutes.   (2)


Subtract equation (1) from equation (2).  You will get

    18x             = 960-600 = 360

      x             = 360/18 = 20  tons.


Next, substitute x = 20 back into equation (1).  You will get

           12y + 12z = 600 - 6*20 = 600 - 120 = 480.


The same equation will be if you substitute x = 60 into equation (2).


So, we, actually, have one single equation for unknown y and z

    12y + 12z = 480.   (3)


It has infinitely many solutions in real positive numbers.

For example, you may give y any value from 0 to 40;  then

    z = 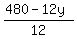 = 40 - y.


So, the problem has infinitely many solutions; based on the condition, it is IMPOSSIBLE
to extract a unique solution.


It is not surprising, since the basic system of equations (1), (2)  has only two equations for 3 unknowns.


In order for the problem admits a unique solution, one more restriction should be added to the problem's formulation.