Question 1205955: You have 37 coins that are nickels, dimes, and pennies. The total value of the coins is $1.55. There are twice as many pennies as dimes. Find the number of each type of coin in the bank.
Found 4 solutions by josgarithmetic, ikleyn, Edwin McCravy, greenestamps:
Answer by josgarithmetic(39617)   (Show Source):
Answer by ikleyn(52786)  (Show Source):
You can put this solution on YOUR website! .
You have 37 coins that are nickels, dimes, and pennies.
The total value of the coins is $1.55.
There are twice as many pennies as dimes.
Find the number of each type of coin in the bank.
~~~~~~~~~~~~~~~~~~~~~~
Let D be the number of dimes.
Then the number of pennies is 2D, according to the problem.
Hence, the number of nickels is (27 - D - 2D) = 37-3D (the remaining coins).
Now write the total money equations, in cents
5*(37-3D) + 10*D + 2D = 155 cents.
+-----------------------------------------------+
| At this point, the setup is just complete. |
+-----------------------------------------------+
Simplify this equation and find D
185 - 15*D + 10*D + 2*D = 155
-3*D = 155 - 185
-3*D = -30
D = 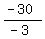 = 10.
ANSWER. 10 dimes, 20 pennies and 37-10-20 = 7 nickels.
CHECK for the total value 10*10 + 20*1 + 7*5 = 155 cents = $1.55. ! correct !
Solved using one equation in one unknown.
Answer by Edwin McCravy(20056)  (Show Source):
You can put this solution on YOUR website!
Let's see why they can't all be nickels.
If all 37 coins were nickels there would be $1.85. So the extra 30 cents must be
2 parts pennies to 1 part dimes or 20 pennies and 10 dimes making 30 coins that
we must reduce the 37 nickels by, so 7 nickels remain.
Edwin
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
From the two formal algebraic solutions you have received, note that the actual work to solve the problem is nearly always easier if you take the time to analyze the problem so it can be set up using a single variable. Plunging in to solving the problem after reading only the first sentence and using three variables leads to a much more complicated solution.
And since I'm always touting the value of the mental exercise you get by solving problems informally using logical reasoning, here is such a solution.
The total value of the coins in cents is a multiple of 5.
The total value of the nickels and dimes is a multiple of 5.
Therefore, the value of the pennies must be a multiple of 5.
But the number of pennies is twice the number of dimes, so the number of pennies must be an even multiple of 5 -- i.e., a multiple of 10.
You can do some deeper logical reasoning to finish the problem; but at this point you have limited the possible solutions to a very few, so looking for a solution using different possible numbers of pennies should be easy.
10 pennies and 5 dimes; that's $0.60 using 15 coins; there would have to be 22 nickels with a total value of $1.55-$0.60 = $0.95. That doesn't work.
20 pennies and 10 dimes; that's $1.20 using 30 coins; that leaves $1.55-$1.20 = $0.35 to be made using 7 nickels. That works.
ANSWER: 20 pennies, 10 dimes, and 7 nickels
|
|
|
