SOLUTION: A plane can travel 1,015 miles in 7 hours traveling against the wind. Traveling with the same wind, the plane can travel 820 miles in 4 hours. How fast can the plane travel in stil

Algebra ->  Coordinate Systems and Linear Equations -> SOLUTION: A plane can travel 1,015 miles in 7 hours traveling against the wind. Traveling with the same wind, the plane can travel 820 miles in 4 hours. How fast can the plane travel in stil      Log On


   

Question 1200756: A plane can travel 1,015 miles in 7 hours traveling against the wind. Traveling with the same wind, the plane can travel 820 miles in 4 hours. How fast can the plane travel in still air and how fast is the wind current?

Found 3 solutions by ikleyn, josgarithmetic, greenestamps:
Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.
A plane can travel 1,015 miles in 7 hours traveling against the wind.
Traveling with the same wind, the plane can travel 820 miles in 4 hours.
How fast can the plane travel in still air and how fast is the wind current?
~~~~~~~~~~~~~~~~ 

Let u be the plane speed in still air,
and let v be the rate of the wind.


The effective speed of the plane with the wind is

    u + v = 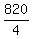820%2F4 = 205 miles per hour.    (1)


The effective speed of the plane against the wind is

    u - v = 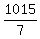1015%2F7 = 145 miles per hour.    (2)


Add equations (1) and (2) and find u

    2u = 205 + 145 = 350,  u = 350/2 = 175 miles per hour (the speed of the plane in still air).


From equation (1), find v

    v = 205 - 175 = 30 miles per hour (the rate of the wind).


ANSWER.  The speed of the plane in still air is 175 miles per hour.

         The rate of the wind is 30 miles per hour.

Solved.



Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
               SPEED         TIME        DISTANCE
AGAINST        r-w            7           1015
WITHWND        r+w            4            820

system%28%28r-w%29%287%29=1015%2C%28r%2Bw%29%284%29=820%29

system%28r-w=1015%2F7%2Cr%2Bw=820%2F4%29

ADDcorrespondingmembers
2r=1015%2F7%2B820%2F4
r=%281%2F2%29%281015%2F7%2B820%2F4%29-----plain, still air
AND
w=%281%2F2%29%28820%2F4-1015%2F7%29----wind

Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


The speed against the wind is 1015/7 = 145 mph; the speed with the wind is 820/4 = 205 mph.

Tutor @ikleyn has shown a standard formal algebraic method for getting from there to finding the speed of the plane and the speed of the wind.

For a quick informal path to the answer (if formal algebra is not required), recognize that the 205 mph is the speed of the plane PLUS the speed of the wind, while the 145 mph is the speed of the plane MINUS the speed of the wind.

Logically that means the speed of the plane is halfway between 205 mph and 145mph, which is 175 mph; then the speed of the wind is the difference between 175 mph and 205 mph (or between 175 mph and 145 mph).

ANSWERS: plane speed 175 mph; wind speed 30 mph