|
Question 752581: How do you graph & compare real numbers and find the absolute value of real numbers?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! To graph and compare real numbers you just plot them on a number line, like this:

The number line is like a ruler, with positive and negative integers marked at regular intervals. Negative numbers are to the left of zero, positive numbers are to the right of zero.
TIP: That is easier to do with paper that already has regularly spaced markings. Grid paper is a good choice. Paper with lines works well if you turn the paper so that the lines run up and down rather than side to side.
COMPARING:
The numbers to the left are smaller than (less than) the numbers to the right, so
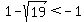 and and 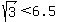 . .
You can turn that around and say that a number than is to the right is larger (greater) than all the numbers to its left.
Negative numbers are to the left of zero, so they are less than zero:
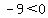 , ,  , , 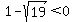 , , 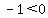 . .
Positive numbers are to the right of zero, so they are less than zero:
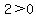 , ,  , , 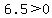 , , 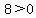 . .
ABSOLUTE VALUE:
Negative numbers are to the left of zero, positive numbers are to the right of zero.
The absolute value of a number is the distance between the number and zero in the graph, and It is always a positive number.
For example,
 with with  is is  unit to the left of zero. unit to the left of zero.
 with with  is is  units to the left of zero. units to the left of zero.
PRACTICAL TIPS:
To figure out where to place a number like  or or 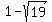 you can calculate an approximate value as a decimal. you can calculate an approximate value as a decimal.
 = -8.571428571428571428571428571428.... = -8.571428571428571428571428571428....
so you can use  (rounded) to figure out where to plot that value. (rounded) to figure out where to plot that value.
The point for  must be must be  units to the left of zero. That's a distance a litle longer than units to the left of zero. That's a distance a litle longer than  units, so you place it a little to the left of the point that is halfway between -8 and -9. units, so you place it a little to the left of the point that is halfway between -8 and -9.
 (rounded) (rounded)
Your calculator may give you the result of that calculation as  , and you know that it is an irrational number with infinite non-repeating digits, but for your purposes, , and you know that it is an irrational number with infinite non-repeating digits, but for your purposes, 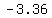 is a good approximation, accurate enough. is a good approximation, accurate enough.
So, when graphing by hand, you plot the point for 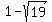 at a distance of about at a distance of about 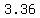 units to the left of zero. You can pretend that units to the left of zero. You can pretend that 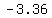 is is
 = -3.333333333... and plot = -3.333333333... and plot 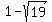 = approximately = approximately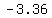  of a unit to the left of of a unit to the left of  . .
|
|
|
| |