|
Question 70768This question is from textbook Introductory and intermediate algebra
: The sum of two numbers is 2. If one number is subtracted from the other, their difference is 8. Find the numbers.
This question is from textbook Introductory and intermediate algebra
Found 3 solutions by mathman409, bucky, Quackpot rocks:
Answer by mathman409(67)   (Show Source): (Show Source):
You can put this solution on YOUR website! the sume of two numbers is 2. if one number is subtracted from the other, their difference is 8. find the numbers.
X+Y=2
X-Y=8
If you subtract X+Y with X-Y, you get 2y, and so that equals 2-8, that is -6.
2y=-6
y=(-6)/2
y=-3
-3+X=2
x=2+3
x=5 and y=-8
Check
-3+5=2
5-(-3)=8
WE DID IT!
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! The first sentence and the last sentence in this problem tell you that you have two unknown
numbers to find. So let's call them by different letters. Normally we would use x and y,
but really we could use any two letters. Just to show you how to work with other letters,
let's call these two numbers A and B.
.
The problem tells you that when you add the two numbers, the answer is 2. So let's write
that as an equation. Adding would be 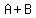 and that equals and that equals  . In equation form . In equation form
that is:
.

.
Next we are told that if one of the numbers is subtracted from the other, the result is 8.
So let's pick one of the numbers and subtract it from the other. Let's subtract B from A.
In algebraic form this would be 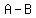 and since this is to equal and since this is to equal  we can we can
write another equation:
.

.
We now have two equations with two unknowns. The fact that there are two independent
equations means that we can solve for the two unknowns. There are several ways to solve
them. Let's use a way called substitution. We'll solve one of the equations for one
of the unknowns in terms of the other, and then we'll substitute that answer into the
other equation to solve it. Hard to explain, but fairly easy to do. Let's try solving
the second equation for A.
.

.
What happens if we add B to both sides of this equation? [Remember whatever we do to one
side of an equation ... adding, subtracting, multiplying, dividing ... we also have to
do to the other side.] When we add +B to the left side it cancels out the -B and the left
side becomes just  . And when we add +B to the right side, the right side becomes . And when we add +B to the right side, the right side becomes
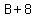 . So we have solved the second equation for A. It is just . So we have solved the second equation for A. It is just  . .
.
Now let's go back to our first equation which was  . From our second equation . From our second equation
we found that  was the same as was the same as 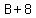 . So in our first equation we can replace the . So in our first equation we can replace the
 with with 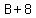 . When we do that the first equation becomes: . When we do that the first equation becomes:
.

.
Adding the B terms together on the left side gives:
.

.
Next add a negative 8 on the left side to get rid of the 8 on the left side. But if we do
that we must also add a negative 8 on the right side. The right side becomes 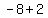
which simplifies to  . So now our equation is: . So now our equation is:
.

.
To solve for just B we divide both sides by 2. The left side becomes just  and the and the
right side is 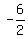 which simplifies to which simplifies to  . So finally we can write this equation . So finally we can write this equation
as:
.

.
We have one of the unknown numbers! Now we can return to either of the original equations.
For example, let's return to  . But we now know that B is -3. So let's substitute . But we now know that B is -3. So let's substitute
-3 for B in this equation. When we do, the equation becomes:
.

.
which becomes:
.

.
To get rid of the -3 on the left side we add +3 to both sides. The result is:
.

.
That's the last thing we had to do. We can now say that the two numbers are  and and  . .
.
Hope this helps you see a way of working problems such as these. As you see, you will need
to be familiar with the rules for algebraic addition, subtraction, multiplication,
and division to work a problem like this. So make sure you learn those rules well.
Answer by Quackpot rocks(6)   (Show Source): (Show Source):
You can put this solution on YOUR website! the sum of two numbers is 2. if one number is subtracted from the other, their difference is 8. find the numbers.
X+Y=2
X-Y=8
If you subtract X+Y with X-Y, you get 2y, and so that equals 2-8, that is -6.
2y=-6
y=(-6)/2
y=-3
-3+X=2
x=2+3
x=5 and y=-8
Check
-3+5=2
5-(-3)=8
WE DID IT! Hope you get better by practicing over time!
|
|
|
| |