Question 696105: determine the slope and y intercept of the problems:y=5x+3, y=-8x-1,y=4+2x,(8,4) and (2,1), (-9,8) and (10,- 4), (-1,-2) and (-3,-4)
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! If you have the equation for a line in the form  ,
called the  form
(or if you can transform the equation you have into that form),
the numbers  and  are the slope and y-intercept respectively.
For  ,  and 
For  ,  and 
For  <--> ,  and 
If you have two points, you can determine the slope and, the y-intercept, and the equation of the line.
I see two simple ways about it:
solve it as a system of equations,
or use what you learned about analytical geometry.
The choice of method depends on your preference (what is easier for you) and your teacher's preference.
USING SYSTEMS OF EQUATIONS:
For the line that passes through (8,4) and (2,1),
substituting  and  (coordinates of (8,4)) into we get
Doing the same with point (2,1), we get
That gives you the system 
that you can solve for and .
Subtracting the second equation from the first, you get
 -->  so 
Substituting that value into , you get
 -->  -->  so 
USING ANALYTICAL GEOMETRY:
The slope of a line is defined as the ratio between the increase in y-coordinate and the increase in x-coordinate when going from one point to the other.
That is easier to write in words than as the usual cumbersome formula, which looks like
for known points  ( , ) and (,).
Then, for any point (x,y) on the line, and a known point ( , )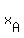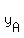
 --> 
gives the equation of the line in the  form,
which can be transformed into the form.
For the line that passes through (8,4) and (2,1),
so as not to get all those numbers mixed up,
you could write into the formula the coordinates of one point at a time.
You may start with point (8,4), with and , and write
 (leaving the spaces for  and  blank).
Then, you could fill in the coordinates of the other point to get
 so
Then you can write the equation of the line in point-slope form,
maybe using point (2,1) as your point:
That can be transformed int the slope intercept form:
--> -->
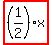
The y-intercept is that invisible  added after the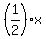 
so .
For the line that passes through (-9,8) and (10,- 4)
Slope=
 --> --> --> -->
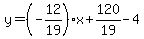So  .
For the line that passes through (-1,-2) and (-3,-4)
Slope=
 --> --> -->
So .
|
|
|
